


General relativity
Dr. Gyula Bene
Department for Theoretical Physics, Loránd Eötvös University
Pázmány Péter sétány 1/A, 1117 Budapest
1. week
Introduction
Literature
Original articles:
- A.Einstein, Die Feldgleichungen der Gravitation, Berl.
Ber. 44 (1915) 844.
Eötvös Loránd szerepe: az Eötvös-kísérlet, 1908-1909.
- R. v. Eötvös, Mathematishe und Naturwissenschaftliche
Berichte aus Ungarn, 8,65,1890.
- R. v. Eötvös, Verhandlungen der 16. Allgemeinen Konferenz
der Internationalen Erdmessung (London-Cambridge, 21-29 September 1909)
- R. v. Eötvös, D. Pekár, E. Fekete: Beiträge zum Gesetz
der Proportionalität von Trägheit und Gravität; a Beneke Alapítványhoz
benyújtott pályamű, 1909.
Preliminaries: special relativity (A.Einstein,
1905)
Events, reference frame, inertial frame
Lorentz transform
$$\begin{align}x'=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}\end{align}$$
$$\begin{align}y'=y\end{align}$$
$$\begin{align}z'=z\end{align}$$
$$\begin{align}t'=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}}\end{align}$$
Maxwell's equations are covariant to Lorentz transforms
$\bf{\rightarrow}$
The velocity of light is independent of the chosen inertial frame. Michelson,
1881, Michelson and Morley, 1887.
The is no distinguished inertial frame (principle of relativity)
$\bf{\rightarrow}$
Lorentz transform expresses a basic symmetry of spacetime.
Interval:
$$\begin{align}s^2=c^2t'^2-{\bf{r'}}^2=c^2t^2-{\bf{r}}^2\end{align}$$
Otherwise:
$$\begin{align}
s^2=g_{ik}x^ix^k
\end{align}$$
where
$$\begin{align}
x^0=ct,\;x^1=x,\;x^2=y,\;x^3=z
\end{align}$$
and
$$\begin{align}
g_{ik}={\rm diag}(1,-1,-1,-1)
\end{align}$$
Proper time:
$$\begin{align}\tau^2=t^2-\bf{r}^2/c^2\end{align}$$
Minkowski space. Timelike, spacelike, lightlike intervals.
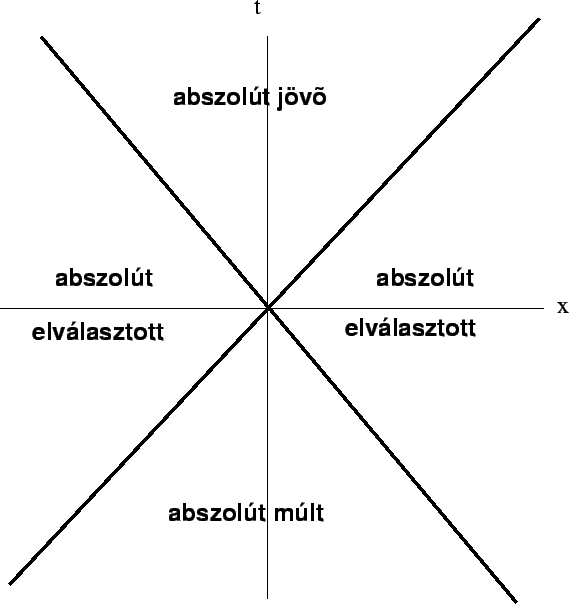
|
Fig. 1. Causal structure of Minkowski space:
light cones separate timelike and spacelike regions.
Time is not absolute: the relativity of simultaneity
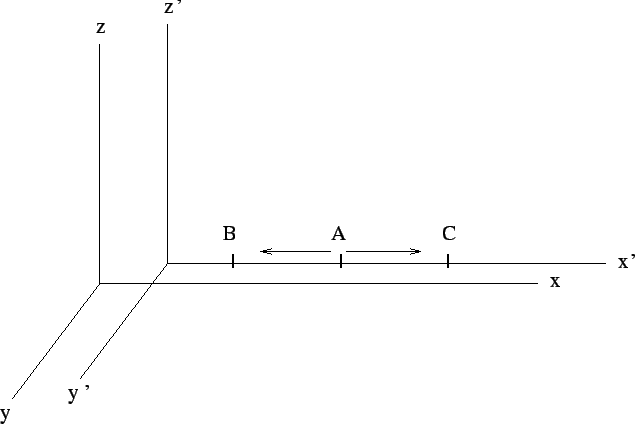
|
Fig. 2. Simultaneity is relative: light signals
arrive at B and C in coordinate frame K' at the same time while in frame K at
different times.
$$\begin{align}
x_1'\ne x_2',\; t_1'=t_2' \bf{\rightarrow} t_1\ne t_2
\end{align}$$
because Lorentz's transform implies
$$\begin{align}
t_2-t_1=\frac{\frac{v}{c^2}(x_2'-x_1')}{\sqrt{1-\frac{v^2}{c^2}}}
\end{align}$$
Lorentz contraction:
The two ends of a moving meter-stick measured in frame K: $(0,0)$
and $(0,L)$ (notation meaning $(t,x)$)
In comoving frame K' the same events are $(0,0)$
and $(t',L_0)$.
Applying Lorentz's transform we have
$$\begin{align}
L_0=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}}\;,
\end{align}$$
i.e.
$$\begin{align}
L=L_0\sqrt{1-\frac{v^2}{c^2}}\;.
\end{align}$$
Time dilatation:
Given pointer states of a moving clock (0 and $\tau$)
measured in frame K : $(0,0)$
and $(t,x)$
In comoving frame K' the same events are $(0,0)$
és $(\tau,0)$
According to Lorentz's transform
$$\begin{align}
t=\frac{\tau}{\sqrt{1-\frac{v^2}{c^2}}}
\end{align}$$
Twin paradox
Transformation of velocities:
$$\begin{align}
v_x=\frac{v'_x+V}{1+\frac{v'_xV}{c^2}}
\end{align}$$
$$\begin{align}
v_y=\frac{v'_y\sqrt{1-\frac{V^2}{c^2}}}{1+\frac{v'_xV}{c^2}}
\end{align}$$
$$\begin{align}
v_z=\frac{v'_z\sqrt{1-\frac{V^2}{c^2}}}{1+\frac{v'_xV}{c^2}}
\end{align}$$
(cf. light aberration, change in the direction of propagation)
Four vectors
Four component quantities transforming like time and space coordinates:
$$\begin{align}t, x, y, z\end{align}$$
$$\begin{align}E, p_x, p_y, p_z\end{align}$$
$$\begin{align}\phi, A_x, A_y, A_z\end{align}$$
Relativistic mechanics:
Four velocity:
$$\begin{align}
u^i=\frac{dx^i}{d\tau}
\end{align}$$
$$\begin{align}
u_x=\frac{v}{c\sqrt{1-\frac{v^2}{c^2}}}
\end{align}$$
$$\begin{align}
u_t=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}
\end{align}$$
Four momentum:
$$\begin{align}
p^i=m u^i
\end{align}$$
Timelike component: energy.
Principle of the least action:
$$\begin{align}
S=-mc\int_a^b ds
\end{align}$$
Lagrangian:
$$\begin{align}
L=-mc^2\sqrt{1-\frac{v^2}{c^2}}
\end{align}$$
In the limit
$c\rightarrow \infty$
one obtains nonrelativistic Newtonian mechanics.
Basic concepts
General relativity implements the demand that laws of physics should be
expressed in any coordinate system (not only in inertial systems) in a
uniform, covariant manner.
This also means that such a description should be possible in accelerating
frames.
Applying special relativity, one concludes that in an accelarating frame the
geometry of space is no longer Eucledian, hence the spacetime geometry is not
Minkowskian, either. Such general geometries are characterized by the metric
tensor.
In general relativity the principle of equivalence plays a central role. It
tells that locally one cannot distinguish between an accelerating frame and a
gravitational field. Since the laws of physics are local laws, spacetime
is also non-Minkowskian in gravitational fields and is described via
some metric tensor.
If the metric tensor is given, other laws of physics can be generalized by
simply substituting derivatives with covariant derivatives.
Gravitational fields are created by masses, or more generally, the source of
gravitational fields is the energy-momentum tensor. This connection is
expressed by Einstein's equations.
Example of an accelarating reference frame: uniformly rotating system of
coordinates
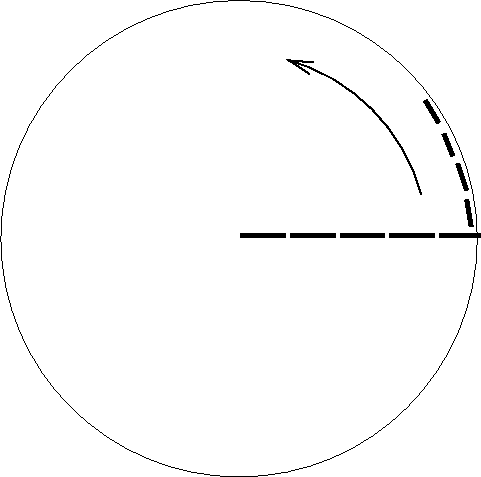 |
Fig. 3. Metre-sticks placed along the
circumference of the rotating disk are Lorentz-contracted, while those
placed along the radius are not effected.
Suppose we are in an inertial frame. Consider a big circular disk of radius
$R$ which rotates with a uniform angular velocity $\omega$ around its symmetry
axis perpendicular to its plane.
Suppose that $R\omega < c$.
There are observers on the disk who measure the length of the perimeter and
radius of the disk by their metre-sticks.
The ratio of the perimeter to the radius would obviously be $2\pi$, if both
quantities were measured in the inertial system,
since lengths were then measured between simultaneous
events (spacetime points). This was equivalent with
mapping the disk to a circle in the inertial frame,
and performing length measurements on that circle.
This ratio is different if the measurement is performed by the observers
staying on the disk. If they measure the perimeter,
their sticks are effected by Lorentz-contraction,
the contraction rate being $\sqrt{1-R^2\omega^2/c^2}$, so
the observers find that the perimeter is $2\pi
R/\sqrt{1-R^2\omega^2/c^2}$ (longer than $2\pi R$),
while they find the radius to be the same $R$ as
measured in the inertial frame. Hence on the disk,
in the co-rotating frame the ratio of perimeter to
radius is $2\pi
/\sqrt{1-R^2\omega^2/c^2}>2\pi$. Thus, in an accelerating frame spatial
geometry is no longer Eucledian, and spacetime geometry is no longer Minkowskian.
Consider the interval between two nearby spacetime points. In the inertial
frame introduce Cartesian spatial coordinates $dx'$, $dy'$, $dz'$ és $dt'$,
and cylindrical coordinates
$dr'$, $d\varphi'$,
$dz'$ és $dt'$. The interval is
$$\begin{align}
ds^2=c^2dt'^2-dx'^2-dy'^2-dz'^2=c^2dt'^2-dr'^2-r'^2d\varphi'^2-dz'^2\;.
\end{align}$$
Let us switch to the frame comoving with the disk by the transformation
$$\begin{align}
t' & = t \\
r' &= r \\
\varphi' &= \varphi +\omega t \\
z' &= z \phantom{forgkr1}
\end{align}$$
This ensures that constant unprimed spatial coordinates describe comoving
points, albeit the physical meaning (relation to measurements) is not obvious.
For the interval we get
$$\begin{align}
ds^2=\left(c^2-r^2\omega^2\right)dt^2-dr^2-r^2d\varphi^2-dz^2-2 r^2\omega d\varphi dt\;.
\end{align}$$
Invariance of the interval was assumed like in special relativity.
Clearly for an arbitrary coordinate transform the interval is a quadratic form
of coordinate differentials:
$$\begin{align}
ds^2=g_{ik}dx^idx^k\;.
\end{align}$$
The quantity $g_{ik}$ is called the metric tensor. In the previous example
with coordinates $x^0=ct$, $x^1=r$, $x^2=\varphi$ and $x^3=z$ we have for
the nonzero components:
$$\begin{align}
g_{00} &= 1-r^2\omega^2/c^2 \\
g_{11} &= g_{33}=-1 \\
g_{22} &= -r^2 \\
g_{02} &= g_{20}=-r^2\omega/c\;.\phantom{forgmetrik1}
\end{align}$$
From the mathematical point of view the metric tensor is a $4\times 4$
symmetric matrix. Signature (signs of the eigenvalues) plays a distinguished
role. A physically meaningful metric must have three negative and one positive
eigenvalues.
Curvilinear coordinates
Az általános relativitáselméletben görbevonalú koordinátákat kell használnunk,
mivel egyrészt
nem-euklideszi geometria esetében nem vezethetők be derékszögű
koordináták, másrészt az elmélet egyik legfontosabb célkitűzése, hogy
tetszőleges koordinátarendszerben is megfogalmazható legyen.
A fenti példához hasonlóan induljunk ki a
$$\begin{align}
ds^2=\left(dx'^0\right)^2-\left(dx'^1\right)^2-\left(dx'^2\right)^2-\left(dx'^3\right)^2\;.
\end{align}$$
Minkowski-metrikából, és térjünk át tetszőleges görbevonalú koordinátákra
(gyorsuló koordinátarendszerre) a
$$\begin{align}
x'^i=x'^i(x^0,x^1,x^2,x^3)
\end{align}$$
képletekkel, ahol a vesszős koordinátákat a vesszőtlenek (általában
nemlineáris) függvényének tekintjük. A koordinátatranszformációt tehát négy
darab négyváltozós függvény adja meg. A koordinátadifferenciálokra a
többváltozós függvények differenciálási szabálya alapján azt kapjuk,
hogy
$$\begin{align}
dx'^i=\frac{\partial x'^i}{\partial x^j}dx^j\;,\phantom{kon_vek}
\end{align}$$
ahol a kétszer előforduló indexekre összegzés értendő. Ezt beírva az
ívelemnégyzet képletébe, a
$$\begin{align}
ds^2=g_{ik}dx^idx^k
\end{align}$$
kvadratikus alak adódik, ahol a $g_{ik}$ metrikus tenzort a
$$\begin{align}
g_{ik}=\frac{\partial x'^l}{\partial x^i}\frac{\partial x'^m}{\partial x^k}g_{lm}^{(0)}\phantom{f1}
\end{align}$$
képlet határozza meg, ahol $g_{lm}^{(0)}={\rm diag}\left(1,-1,-1,-1\right)$ a
Minkowski-metrikának megfelelő metrikus tenzor. Mivel a transzformáció
általában nemlineáris, a $g_{ik}$ metrikus tenzor komponensei téridő-pontról
téridő-pontra változnak, azaz függnek a koordinátáktól. A (\ref{f1}) képlet megfordítva azt jelenti,
hogy gyorsuló koordinátarendszerből alkalmas koordinátatranszformációval a
téridő minden pontjában a metrikus tenzor egyidejűleg a Minkowski-metrikára
transzformálható. Ez a tulajdonság tömegek által keltett gravitációs terekben
már nem érvényes, semmilyen koordinátatranszformációval nem hozható mindenütt
egyidejűleg sík (Minkowski) alakra a metrika. Emiatt ilyenkor görbült
téridőről beszélünk, hiszen a nem-Minkowski alak nem pusztán a választott
koordinátarendszer, hanem a téridő tulajdonsága. Hogy általános esetben a
metrikus tenzort nem lehet mindenütt Minkowski-alakra transzformálni, már abból
is nyilvánvaló, hogy a szimmetrikus $4\times 4$-es metrikus tenzornak tíz
független eleme van, melyek a téridő függvényei, de az általános
koordinátatranszformációban csak négy függvény szerepel.
\par\medskip
A (\ref{f1}) képlet
megfordításával a vesszős koordinátarendszer-beli metrikus tenzor kifejezése
$$\begin{align}
g'_{lm}=\frac{\partial x^i}{\partial x'^l}\frac{\partial x^k}{\partial x'^m}g_{ik}\;.\phantom{f2}
\end{align}$$
Látható, hogy a metrikus tenzor indexei másképpen transzformálódnak, mint a
koordinátadifferenciálok. Vizsgáljuk meg, hogyan transzformálódik egy $\Phi(\{x^{i}\})$
skalárfüggvény
gradiense! A közvetett függvény deriválási szabálya szerint azt kapjuk, hogy
$$\begin{align}
\frac{\partial \Phi}{\partial x'^i}=\frac{\partial x^j}{\partial x'^i}\frac{\partial \Phi}{\partial x^j}\;,\phantom{kov_vek}
\end{align}$$
A koordinátadifferenciálok homogén lineáris transzformációs szabálya szerint
transzformálódó mennyiségeket a továbbiakban kontravariáns vektoroknak
nevezzük, a skalár gradiensének (szintén homogén lineáris) transzformációs szabálya szerint
transzformálódó mennyiségeket pedig kovariáns vektornak. A transzformációs
szabályt az index pozíciójával jelezzük: a felső index kontravariáns, az alsó
index kovariáns vektorkomponensként transzformálódó mennyiséget jelent. Látható, hogy a
metrikus tenzor indexei egyenként kovariáns vektorként
transzformálódnak. Általában tenzornak nevezünk majd olyan többindexes mennyiségeket,
amelyek kontravariáns és/vagy kovariáns vektorkomponensek szorzataként transzformálódnak.
A
kétféle transzformációs szabály együtthatómátrixai éppen egymás inverzei,
emiatt egy kovariáns és egy kontravariáns vektor szorzata az indexeket
összeejtve (azaz egyenlővé téve és az egyenlő indexre összegezve) skalárt
eredményez:
$$\begin{align}
A'^iB'_i=\frac{\partial x'^i}{\partial x^k}A^k\frac{\partial x^n}{\partial x'^i}B_n=A^kB_k\;.\phantom{gk1}
\end{align}$$
Tenzorok esetén egy kovariáns és egy kontravariáns index
összeejtése a tenzor rendjét kettővel csökkenti.
Egy $A^i$ kontravariáns vektort a kovariáns $g_{ik}$
metrikus tenzorral megszorozva és indexét annak egyik indexével összeejtve
kovaráns vektort kapunk, amit $A_i$-vel jelölünk, mivel ugyanannak a fizikai
mennyiségnek a kovariáns változata:
$$\begin{align}
A_i=g_{ik}A^k\;.\phantom{gk2}
\end{align}$$
Fordítva, egy kovariáns vektort $g_{ik}$
inverzével szorozva indexösszeejtéssel kontravariáns vektort kapunk. A
metrikus tenzor inverzét $g^{ik}$-val jelöljük és kontravariáns metrikus
tenzornak nevezzük:
$$\begin{align}
A^i&=g^{ik}A_k\;,\phantom{gk3a}\\
g^{ik}g_{kj}&=\delta^i_j\;.\phantom{gk3b}
\end{align}$$
A kovariánsból kontravariáns mennyiség előállítását
röviden az index felhúzásának, a fordított műveletet az index lehúzásának
fogjuk hívni.
Distances and elapsed times, proper physical quantities
Általános görbevonalú koordinátarendszerben a koordináták csupán az események
téridőbeli helyzetét határozzák meg, de különbségeik nem felelnek meg valódi
távolságoknak ill. időtartamoknak. Ez önmagában nem meglepő, hiszen ez a
helyzet pl. térbeli polárkoordináták használatakor is. Felmerül tehát a
kérdés, hogy a metrika ismeretében hogyan határozható meg két közeli esemény
valódi távolsága ill. a tér adott pontjában végbemenő két esemény között
eltelt valódi időtartam. Általánosabban felvethető az a kérdés, hogy mi a
kapcsolat a tényleges, mérhető fizikai mennyiségek és a leírásukra használt
vektor vagy tenzorkomponensek között.
\par\medskip
A megoldás alapja ugyanaz, amit már a forgó korongon végzett méréseknél is
hangsúlyoztam: a koordinátarendszer adott pontjában áttérünk egy olyan
inerciarendszerre, ami a görbevonalú koordinátarendszer adott pontjával az
adott pillanatban együtt mozog, és minden mérhető mennyiséget ebben az
érintőtérben értelmezünk. Távolságok és időtartamok mérésekor nem egy, hanem
két közeli pontról (eseményről) van szó, azonban a leírt konstrukcióban a
másik pont sebessége az inerciarendszerhez képest másodrendben kicsi (a koordinátakülönségek négyzetével arányos).
Elapsed time between events which happened at the same spatial point
A két esemény a leírt konstrukcióval felvett inerciarendszerben is azonos
helyen van, így a közöttük eltelt valódi $d\tau$ idővel az ívelemnégyzet
$$\begin{align}
ds^2=c^2d\tau^2
\end{align}$$
alakban fejezhető ki. A görbevonalú koordinátarendszerben a két esemény
közötti ívelemnégyzet ugyanennyi, viszont a görbevonalú koordinátákkal
fejezhető ki:
$$\begin{align}
ds^2=g_{00}\left(dx^0\right)^2\;,
\end{align}$$
ugyanis a térbeli koordináták különbségei eltűnnek ($dx^\alpha =0$). A két kifejezés egyenlőségéből
$$\begin{align}
d\tau=\frac{\sqrt{g_{00}}}{c}dx^0
\end{align}$$
adódik.
Spatial distance between events
Áttérünk az inerciarendszerre, melyben az egyidejűség fogalma jól
meghatározott, mivel az idő egyformán telik a különböző térbeli pontokban.
Ez azt jelenti, hogy olyan konstans együtthatós, homogén lineáris
transzformációt alkalmazunk, ami a kiszemelt téridőpontban
Minkowski-alakra hozza a metrikát. Ezenkívül, hogy az inerciarendszer ne mozogjon
a görbevonalú koordinátarendszerhez képest, megköveteljük, hogy az
inerciarendszerbeli $dx'^\alpha$ térbeli koordinátadifferenciálok ne
függjenek $dx^0$-tól. Ekkor ugyanis $dx^\alpha=0$-ból $dx'^\alpha=0$
következik (és viszont), tehát az egyik rendszerben rögzített térbeli pont a
másikban is helyben marad. Ez annyit jelent matematikailag, hogy a
koordinátadifferenciálok transzformációs képlete
$$\begin{align}
dx'^\alpha&=A^\alpha_\beta dx^\beta\phantom{transz1}\\
dx'^0&= A^0_j dx^j\;.\phantom{transz2}
\end{align}$$
A görög betűk a térbeli (1,2,3), a latin betűk a téridőbeli
(0,1,2,3) indexeken futnak végig. Az ívelemnégyzet
$$\begin{align}
ds^2=\left(dx'^0\right)^2-\left(dx'^\alpha\right)^2=A^0_j A^0_k
dx^jdx^k-A^\alpha_\beta A^\alpha_\nu dx^\beta dx^\nu\;.
\end{align}$$
Ez természetesen meg kell, hogy egyezzen a $g_{jk}dx^jdx^k$ kifejezéssel. A
térszerű és időszerű indexek szétválasztásával ez azt jelenti, hogy
$$\begin{align}
g_{00}&=\left(A^0_0\right)^2\phantom{g00}\\
g_{0\alpha}&=A^0_0A^0_\alpha\phantom{g01}\\
g_{\beta\nu}&=A^0_\beta A^0_\nu - A^\alpha_\beta A^\alpha_\nu\;.\phantom{g11}
\end{align}$$
Az első egyenletből
$$\begin{align}
A^0_0=\sqrt{g_{00}}\;,\phantom{a00}
\end{align}$$
a másodikból pedig
$$\begin{align}
A^0_\alpha=\frac{g_{0\alpha}}{\sqrt{g_{00}}}\phantom{a01}
\end{align}$$
adódik. Két közeli pont $d\ell$ távolságának mérésekor az inerciarendszerben
egyidejű pontokat vizsgálunk, vagyis megköveteljük, hogy $dx'^0=0$ legyen, ezért
egyrészt
$$\begin{align}
ds^2=-\left(d\ell\right)^2\phantom{tav1}
\end{align}$$
írható, másrészt megkapjuk az egyidejűség feltételét a görbevonalú
koordinátarendszerben:
$$\begin{align}
dx'^0= A^0_j dx^j=0\;.
\end{align}$$
Ebbe a transzformáció mátrixát behelyettesítve kapjuk, hogy
$$\begin{align}
dx^0=-\frac{g_{0\alpha}}{g_{00}}dx^\alpha\;.\phantom{szink1}
\end{align}$$
Két közeli esemény tehát akkor egyidejű, ha időkoordinátáik különbségére ez az
egyenlet teljesül. Az egyidejűség feltételének megadását szokás szemléletesen
az órák szinkronizálásának nevezni. Az eljárást folytatva további pontokra definiálható az
események egyidejűsége, így egy
görbe mentén is. Az viszont már általában nem igaz, hogy zárt görbe mentén az
órák szinkronizálása elvégezhető, ugyanis a kezdőpontba visszatérve véges
időkoordináta-különbség adódik. Más szavakkal, két véges távolságban levő pont
egyidejűsége nem definiálható egyértelműen, mivel az órák szinkronizálásának
eredménye általában függ attól, hogy a két pont között milyen pálya mentén
végeztük el a szinkronizálást. Ez a helyzet például a forgó koordinátarendszer
esetén: az origó középpontú kör mentén szinkronizálva az órákat nulla
helyett
$$\begin{align}
\Delta x^0=-\oint \frac{g_{0\alpha}}{g_{00}}dx^\alpha=\frac{2\pi R^2\omega c}{c^2-R^2\omega^2}
\end{align}$$
adódik. Ez a tulajdonság nem a téridő, hanem a választott koordinátarendszer
tulajdonsága. Nyilvánvaló, hogy a négy transzformációs függvény (vagyis a
koordinátarendszer) alkalmas megválasztásával általában a téridő minden
pontjában nullává tehető a három $g_{0\alpha}$ mennyiség, sőt még az is
elérhető, hogy ezzel egyidejűleg minden téridő-pontban $g_{00}=1$ is
teljesüljön. Az ilyen koordinátarendszert, melyben az egyidejűség a teljes
téridőben egyértelműen definiálható, szinkronizált vonatkoztatási rendszernek,
az $x^0$ időkoordinátát, melynek különbsége az adott térbeli pontban eltelt
valódi idővel egyenlő, világidőnek nevezzük. \footnote{Az előbbi állítást annyiban pontosítanunk kell, hogy szinkronizált
vonatkoztatási rendszerben a világidő valamilyen véges értékénél a metrika
szükségképpen szingulárissá válik, azon túl (pozitív vagy negatív időirányban)
a koordinátarendszer nem alkalmazható. }
\par\medskip
Visszatérve a közeli pontok valódi távolságához, a (\ref{tav1}) és
(\ref{szink1}) képletekből azt kapjuk, hogy
$$\begin{align}
\left(d\ell\right)^2&=-ds^2=-g_{00}\left(dx^0\right)^2-2g_{0\alpha}dx^0dx^\alpha-g_{\alpha\beta}dx^\alpha
dx^\beta \\
&=\left(\frac{g_{0\alpha}g_{0\beta}}{g_{00}}-g_{\alpha\beta}\right)dx^\alpha
dx^\beta\;.
\end{align}$$
A
$$\begin{align}
\gamma_{\alpha\beta} =\frac{g_{0\alpha}g_{0\beta}}{g_{00}}-g_{\alpha\beta}\phantom{gamma}
\end{align}$$
mennyiség tehát a térbeli metrikát határozza meg. Érdekesség, hogy ez éppen a
$-g^{\alpha\beta}$ $3\times 3$-as mátrix (a kontravariáns metrikus tenzor
térszerű részének ellentettje) inverze.
\par\medskip
A forgó koordinátarendszer (\ref{forgmetrik1}) téridő-metrikájának
segítségével a forgó korong térbeli metrikájának nullától különböző komponenseire
a
$$\begin{align}
\gamma_{11}&=1 \\
\gamma_{22}&=\frac{r^2}{1-\frac{r^2\omega^2}{c^2}} \\
\gamma_{33}&=1\phantom{forgmetrik2}
\end{align}$$
értékeket kapjuk. Ennek megfelelően a sugárirányú valódi távolság a korong
közepétől a pereméig $R$, míg a perem mentén mérve a valódi kerület $2\pi
R/\sqrt{1-R^2\omega^2/c^2}$, a korábbi eredménnyel egyezően.
Proper physical quantities
Valamely lokális fizikai mennyiséget, amely lehet skalár, vektor, tenzor, az
elméletben tetszőleges görbevonalú komponenseivel megadhatunk, az indexeket a
metrikus tenzorral ill. inverzével le- és felhúzhatjuk. Természetes módon
merül fel a kérdés, hogy mi felel meg a ténylegesen mérhető értékeknek. A
válasz azt, hogy a (\ref{transz1}), (\ref{transz2}) képletekkel - mivel ez
egyben a kontravariáns vektorkomponensek transzformációs szabálya is -, vagy ennek
inverzével (kovariáns vektorok esetében), vagy ezek szorzatával (tenzorok
esetén) inerciarendszerbe képezzük le kérdéses fizikai mennyiséget, és
eredményül a ténylegesen mérhető értéket kapjuk. A transzformáció megadásához
szükségünk van az eddig még nem meghatározott $A^\alpha_\beta$ mennyiségekre
is. A megadott feltételek alapján ez nem egyértelmű, ami azzal kapcsolatos,
hogy az inerciarendszer $x$, $y$, $z$ térszerű koordinátatengelyeit még
tetszőleges forgatásnak lehet alávetni. Az (\ref{g11}), (\ref{gamma})
egyenletekből ugyanis
$$\begin{align}
A^\alpha_\beta A^\alpha_\nu=\gamma_{\beta\nu}\phantom{transz2a}
\end{align}$$
adódik, aminek a megoldása
$$\begin{align}
A^\alpha_\beta =F^\alpha_\nu\sqrt{\lambda_\nu} O^\nu_\beta \;,\phantom{transz3}
\end{align}$$
ahol $F^\alpha_\nu$ tetszőleges $3\times 3$-as ortogonális mátrix
(forgásmátrix), $\lambda_\nu$ a $\gamma_{\alpha\beta}$ pozitív definit, valós
szimmetrikus mátrix $\nu$-edik sajátértéke, $O^\nu_\beta$ pedig a hozzátartozó
sajátvektor, melyek összessége szintén $3\times 3$-as ortogonális mátrixot
alkot.
\par\medskip
Fejezzük ki pl. egy forgó korongon mozgó tömegpont sebességét koordinátáinak
időderiváltjaival! Jelöljük a $t$ szerinti
deriváltakat $\dot{r}$, $\dot{\varphi}$ és $\dot{z}$-tal! Először a
négyessebességet írjuk fel, ami definíció szerint $u^i=dx^i/ds$, azaz
$$\begin{align}
u^0&=\frac{dx^0}{ds}=\frac{1}{\sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}}
\\
u^1&=\frac{dx^1}{ds}=\frac{\dot{r}}{c\sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}} \\
u^2&=\frac{dx^2}{ds}=\frac{\dot{\varphi}}{c \sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}}\\
u^3&=\frac{dx^3}{ds}=\frac{\dot{z}}{c\sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}}
\end{align}$$
A (\ref{transz1}), (\ref{transz2}), (\ref{a00}), (\ref{a01}), (\ref{transz3})
képleteket alkalmazzuk. Mivel a (\ref{forgmetrik2}) térbeli metrika máris
diagonális, az $O^\nu_\beta$ mátrix az egységmátrix, a $\lambda_\nu$ értékek
pedig a diagonális elemek. Végül az $F^\alpha_\nu$ forgásmátrixot önkényesen
egységmátrixnak választjuk. Ekkor az $A^\alpha_\beta$ transzformációs mátrix
diagonális lesz. Mindezeket figyelembevéve a négyessebesség komponenseit
$$\begin{align}
u'^0&=\frac{dx'^0}{ds}=\frac{1-\frac{r^2\omega^2}{c^2}-\frac{r^2\omega\dot{\varphi}}{c^2}}{\sqrt{1-\frac{r^2\omega^2}{c^2}}\sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}} \\
u'^1&=\frac{dx'^1}{ds}=\frac{\dot{r}}{c\sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}} \\
u'^2&=\frac{dx'^2}{ds}=\frac{r\dot{\varphi}}{c\sqrt{1-\frac{r^2\omega^2}{c^2}}\sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}} \\
u'^3&=\frac{dx'^3}{ds}=\frac{\dot{z}}{c\sqrt{1-\frac{\dot{r}^2}{c^2}-\frac{r^2\left(\dot{\varphi}+\omega\right)^2}{c^2}-\frac{\dot{z}^2}{c^2}}}
\end{align}$$
alakban kapjuk. Ez az elmozdulásokat a tömegpont sajátidejében méri, amint az
a négyessebesség esetében szokásos. A hármassebesség komponenseit viszont
korongon eltelt valódi időben mérjük, mégpedig a tömegpont pályája mentén
szinkronizált órák segítségével. Ez azt jelenti, hogy az eltelt valódi idő
nagysága $dx^0$
időkoordináta-változáskor
$$\begin{align}
\sqrt{g_{00}}\left(dx^0+\frac{g_{0\alpha}}{g_{00}}dx^\alpha\right)
\end{align}$$
lesz, mivel figyelembe kell vennünk, hogy a másik térbeli pontban a 0 időpont
$-\frac{g_{0\alpha}}{g_{00}}dx^\alpha$-val
egyidejű. De ez azt jelenti, hogy éppen $dx'^0$ (v.ö. (\ref{transz2})) szerint
kell a koordinátákat deriválni. Így viszont a keresett hármassebesség-komponensek
$$\begin{align}
v^1&=c\frac{u'^1}{u'^0}=\frac{\dot{r}\sqrt{1-\frac{r^2\omega^2}{c^2}}}{1-\frac{r^2\omega^2}{c^2}-\frac{r^2\omega\dot{\varphi}}{c^2}} \\
v^2&=c\frac{u'^2}{u'^0}=\frac{r\dot{\varphi}}{1-\frac{r^2\omega^2}{c^2}-\frac{r^2\omega\dot{\varphi}}{c^2}}\\
v^3&=c\frac{u'^3}{u'^0}=\frac{\dot{z}\sqrt{1-\frac{r^2\omega^2}{c^2}}}{1-\frac{r^2\omega^2}{c^2}-\frac{r^2\omega\dot{\varphi}}{c^2}}
\end{align}$$


 bene@arpad.elte.hu
bene@arpad.elte.hu



