General relativity

Dr. Gyula Bene
Department for Theoretical Physics, Loránd Eötvös University
Pázmány Péter sétány 1/A, 1117 Budapest
11. week

Experimental evidence of general relativity I.

Experimental evidence of principle of equivalence. Perihelion precession. Light deflection in gravitational field. Comparison with Newtonian gravity. Gravitational redshift. Gravity Probe B experiment. Gravitational waves, Hulse-Taylor pulsar.

Experimental evidence of principle of equivalence

The principle of equivalence plays a key role in general relativity. The principle states that inertial forces and gravitational forces are locally equivalent. This also means that gravitational force acting on a body is proportional to its inertial mass and does not depend on its other properties. This assumption may be checked experimentally. If inertial mass is equal to gravitating mass, then motion in a gravitational field is independent of mass and other features of matter. This is why drop experiments and pendulum experiments are suitable for that check. Torsion balance on the rotating Earth measures the sum of the centrifugal force and gravity. The differences in horizontal components of this force create a torque that twists a thin metal wire. The angle of this twist is measured. The Eötvös pendulum, when performing the measurement in several rotated positions (around vertical axis) of the intrument, allows determination of second mixed derivatives of the Newtonian gravitational potential together with its Laplacian, \(\triangle \phi\). If there were differences (depending on material properties) between inertial (cf. centrifugal force) and gravitating masses, performing the mesurement with different materials, one would get different results. The method of Eötvös had an exceptional scientific impact in his days, beyond its practical geophysical application (note that the largest oilfield of US was discovered by using the Eötvös torsion balance). The accuracy of the torsion balance was further increased by a factor of 25 (János Renner - disciple and former coworker of Eötvös - , 1935). The currently most accurate measurement further decreased the error with four digits. Hence, the identity of inertial mass and gravitating mass are equal to a relative precision of 13 digits.

A compilation of Ciufolini és Wheeler about the measurements performed:

Year	Investigator	Accuracy	Method
500?	Philoponus	"small"	drop tower
1585	Stevin	\(5\times 10^{-2}\)	drop tower
1590?	Galileo	\(2\times10^{-2}\)	pendulum, drop tower
1686	Newton	\(10^{-3}\)	pendulum
1832	Bessel	\(2\times10^{-5}\)	pendulum
1910	Southerns	\(5\times10^{-6}\)	pendulum
1918	Zeeman	\(3\times10^{-8}\)	torsion balance
1922	Eötvös	\(5\times10^{-9}\)	torsion balance
1923	Potter	\(3\times10^{-6}\)	pendulum
1935	Renner	\(2\times10^{-10}\)	torsion balance
1964	Dicke,Roll,Krotkov	\(3\times10^{-11}\)	torsion balance
1972	Braginsky,Panov	\(10^{-12 }\)	torsion balance
1976	Shapiro, et al.	\(10^{-12 }\)	lunar laser ranging
1981	Keiser,Faller	\(4\times10^{-11 }\)	fluid support (swimming torsion balance with electrostatic restoring torque)
1987	Niebauer, et al.	\(10^{-10 }\)	drop tower
1989	Heckel, et al.	\(10^{-11}\)	torsion balance
1990	Adelberger, et al.	\(10^{-12}\)	torsion balance
1999	Baessler, et al.	\(5\times10^{-14 }\)	torsion balance

Perihelion precession

Perihelion precession in weak gravitational field: The classic Newtonian \(1/r\) potential gets a \(1/r^3\) correction, hence orbits do not close. The closest point to the Sun - perihelion - slowly wanders, in one orbital revolution to an amount of \[\begin{align} \delta \varphi&=2\int_{r_{min}}^{r_{max}} \frac{J\;dr}{r^2\sqrt{\left(\left(\frac{E}{c}\right)^2-m^2c^2\right)+\frac{2km^2M}{r}-\frac{J^2}{r^2}+\frac{2kMJ^2}{c^2}\frac{1}{r^3}}}-2\pi \\ &=\frac{6\pi k^2 m^2 M^2}{c^2 J^2}=\frac{6\pi k M}{c^2 a(1-e^2)} \end{align}\] here \(a\) stands for the half major axis of the elliptic orbit, \(e\) for its excentricity.

Proof: \[\begin{align} \delta \varphi&=2\int_{r_{min}}^{r_{max}} \frac{J\;dr}{r^2\sqrt{\left(\left(\frac{E}{c}\right)^2-m^2c^2\right)+\frac{2km^2M}{r}-\frac{J^2}{r^2}+\frac{2kMJ^2}{c^2}\frac{1}{r^3}}}-2\pi \end{align}\] Let \(E'=\frac{1}{2m}\left(\left(\frac{E}{c}\right)^2-m^2c^2\right)\approx E-mc^2\). In case of bounded motion this is negative. Futher, let us denote the coefficient \(\frac{2kMJ^2}{c^2}\) by \(\beta\).

\(r_{min}\) and \(r_{max}\) are return points of the orbit, i.e., zeros of the expression below the square root. These are approximately (by neglecting the correction term \(\beta/r^3\)): \[\begin{align} \frac{1}{r_{min}}&\approx \frac{km^2M}{J^2}\left(1+\sqrt{1+\frac{2E'J^2}{k^2m^3M^2}}\right)\\ \frac{1}{r_{max}}&\approx \frac{km^2M}{J^2}\left(1-\sqrt{1+\frac{2E'J^2}{k^2m^3M^2}}\right) \end{align}\] Since \(E'<0\), both values are positive.

Now \[\begin{align} \delta \varphi&=-2\pi+2\int_{r_{min}}^{r_{max}} \frac{J\;dr}{r^2\sqrt{2mE'+\frac{2km^2M}{r}-\frac{J^2}{r^2}+\frac{\beta}{r^3}}} \\ &=-2\pi-2\frac{\partial }{\partial J}\left(\int_{r_{min}}^{r_{max}}dr\sqrt{2mE'+\frac{2km^2M}{r}-\frac{J^2}{r^2}+\frac{\beta}{r^3}}\right) \end{align}\] Let us expand the integrand in terms of \(\beta \) to first order. The zeroth term vanishes since \[\begin{align} &-2\pi-2\frac{\partial }{\partial J}\left(\int_{r_{min}}^{r_{max}}dr\sqrt{2mE'+\frac{2km^2M}{r}-\frac{J^2}{r^2}}\right) \\ =&-2\pi+2\int_{r_{min}}^{r_{max}} \frac{J\;dr}{r^2\sqrt{2mE'+\frac{2km^2M}{r}-\frac{J^2}{r^2}}} \\ =&-2\pi+2\int_{J/r_{max}}^{J/r_{min}} \frac{d\xi}{\sqrt{2mE'+\frac{2km^2M}{J}\xi-\xi^2}} \\ &\left(\text{here }\xi=\frac{J}{r}\right) \\ =&-2\pi+2\int_{J/r_{max}}^{J/r_{min}} \frac{d\xi}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}-\left(\xi-\frac{km^2M}{J}\right)^2}} \\ =&-2\pi+2\int_{\zeta_1}^{\zeta_2} \frac{d\zeta}{\sqrt{1-\zeta^2}} \\ &\left(\text{here }\zeta=\frac{\xi-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}\;,\quad \zeta_1=\frac{\frac{J}{r_{max}}-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}=-1\;,\quad \zeta_2=\frac{\frac{J}{r_{min}}-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}=1 \right) \\ =&-2\pi+2\int_{-1}^{1} \frac{d\zeta}{\sqrt{1-\zeta^2}}=-2\pi+2\left.\arcsin\zeta\phantom{\frac{1}{1}}\right|_{-1}^1=0. \end{align}\] In first order: \[\begin{align} \delta \varphi&=-\beta\frac{\partial }{\partial J}\left(\int_{r_{min}}^{r_{max}}\frac{dr}{r^3\sqrt{2mE'+\frac{2km^2M}{r}-\frac{J^2}{r^2}}}\right) \\ &=-\beta\frac{\partial }{\partial J}\left(\frac{1}{J^2}\int_{J/r_{max}}^{J/r_{min}}\frac{\xi\;d\xi}{\sqrt{2mE'+\frac{2km^2M}{J}\xi-\xi^2}}\right) \\ &\left(\text{here }\xi=\frac{J}{r}\right) \\ &=-\beta\frac{\partial }{\partial J}\left(\frac{1}{J^2}\int_{J/r_{max}}^{J/r_{min}} \frac{\xi\;d\xi}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}-\left(\xi-\frac{km^2M}{J}\right)^2}}\right) \\ &=-\beta\frac{\partial }{\partial J}\left(\frac{1}{J^2}\int_{\zeta_1}^{\zeta_2} \frac{\left(\frac{km^2M}{J}+\zeta\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}\right)\;d\zeta}{\sqrt{1-\zeta^2}}\right) \\ &\left(\text{here }\zeta=\frac{\xi-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}\;,\quad \zeta_1=\frac{\frac{J}{r_{max}}-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}=-1\;,\quad \zeta_2=\frac{\frac{J}{r_{min}}-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}=1 \right) \\ &=-\beta\frac{\partial }{\partial J}\left(\frac{km^2M}{J^3}\underbrace{\int_{-1}^{1} \frac{d\zeta}{\sqrt{1-\zeta^2}}}_{=\pi}+\frac{1}{J^2}\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}\underbrace{\int_{-1}^{1} \frac{\zeta\;d\zeta}{\sqrt{1-\zeta^2}}}_{=0}\right) \\ &=\beta\frac{3\pi km^2M}{J^4} \\ &=\frac{6\pi k^2m^2M^2}{c^2 J^2}=\frac{6\pi k M}{c^2 a(1-e^2)} \end{align}\] This last equality contains parameters of the unperturbed orbit, half major axis \(a\) and excentricity \(e\). Unperturbed orbit: \[\begin{align} \varphi&=\int_{r}^{r_{max}}\frac{J\;dr}{r^2\sqrt{2mE'+\frac{2km^2M}{r}-\frac{J^2}{r^2}}} \\ &=\int_{J/r_{max}}^{J/r} \frac{d\xi}{\sqrt{2mE'+\frac{2km^2M}{J}\xi-\xi^2}} \\ &\left(\text{here }\xi=\frac{J}{r}\right) \\ &=\int_{J/r_{max}}^{J/r} \frac{d\xi}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}-\left(\xi-\frac{km^2M}{J}\right)^2}} \\ &=\int_{\zeta_1}^{\zeta} \frac{d\zeta}{\sqrt{1-\zeta^2}} \\ &\left(\text{here }\zeta=\frac{\xi-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}\;,\quad\zeta_1=\frac{\frac{J}{r_{max}}-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}=-1 \right) \\ &=\int_{-1}^{\zeta} \frac{d\zeta}{\sqrt{1-\zeta^2}}=\pi-\arccos\zeta \end{align}\] Assuming that \(\zeta\in(-1,1)\) and \(\varphi\in (0,\pi)\), the above equation implies \[\begin{align}\zeta=\cos(\pi-\varphi)=-\cos\varphi\;,\end{align}\] i.e. \[\begin{align}\frac{\frac{J}{r}-\frac{km^2M}{J}}{\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}}=-\cos\varphi\;.\end{align}\] This implies \[\begin{align} \frac{J}{r}= \frac{km^2M}{J}-\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}\cos\varphi\;, \end{align}\] or \[\begin{align} \frac{1}{r}= \frac{km^2M}{J^2}\left(1-\frac{J}{km^2M}\sqrt{2mE'+\frac{k^2m^4M^2}{J^2}}\cos\varphi\right) \end{align}\] This is equation of an ellipse with parameter \[\begin{align}p=\frac{J^2}{km^2M}\end{align}\] and excentricity \[\begin{align}e=\sqrt{1+\frac{2E'J^2}{k^2m^3M^2}}\;.\end{align}\] In terms of these we have \[\begin{align}r=\frac{p}{1-e\cos\varphi}\end{align}\] The half length of the major axis (from the center to the farthest point) \[\begin{align}a=\frac{1}{2}\left(\frac{p}{1-e\cos 0}+\frac{p}{1-e\cos\pi}\right)=\frac{1}{2}\left(\frac{p}{1-e}+\frac{p}{1+e}\right)=\frac{p}{1-e^2}\end{align}\] This leads to \[\begin{align}\frac{J^2}{km^2M}=p=a(1-e^2)\end{align}\] and hence \[\begin{align}\delta \varphi=\frac{6\pi k^2m^2M^2}{c^2 J^2}=\frac{6\pi k M}{c^2 a(1-e^2)}\end{align}\] Perihelion precession is largest for the Mercur among the planets. Current most accurate radar measurements give that Mercur's perihelion precession in a frame attached to the center of the Solar system amount to \(574.10\pm 0.65\) in hundred years. This is due to the following reasons:

Amount (arcsec/century)	Cause
\(531.63 \pm 0.69\)	Gravity of other planets
\(0.0254\)	Oblateness of Sun (quadrupole momentum)
\(42.98 \pm 0.04\)	General relativity
\(574.64\pm 0.69\)	Sum
\(574.10\pm 0.65\)	Measurement

Hence, taking into account contribution of general relativity theoretical value agrees with measurement within measurement error.

Light deflection in gravitational field

Gravitational field deflects light rays. The change of direction in a weak field: \[\begin{align} \delta \varphi&=2\int_{r_{min}}^{\infty} \frac{\rho\;dr}{r^2\sqrt{1-\frac{\rho^2}{r^2}+\frac{2kM \rho^2}{c^2}\frac{1}{r^3}}}-\pi \\ &=\frac{2r_g}{\rho}=\frac{4kM}{c^2 \rho} \end{align}\] Proof: Let \(r_{min}\approx \rho\) and \(\beta'=\frac{2kM \rho^2}{c^2}\). Then \[\begin{align} \delta \varphi&=2\int_{r_{min}}^{\infty} \frac{\rho\;dr}{r^2\sqrt{1-\frac{\rho^2}{r^2}+\frac{\beta'}{r^3}}}-\pi \\ &=-\pi-2\frac{\partial }{\partial \rho}\left(\int_{r_{min}}^{\infty}dr\sqrt{1-\frac{\rho^2}{r^2}+\frac{\beta'}{r^3}}\right) \\ &(\beta'\text{ to be considered a constant during derivation)} \\ &=-\beta'\frac{\partial }{\partial \rho}\left(\int_{\rho}^{\infty}\frac{dr}{r^3\sqrt{1-\frac{\rho^2}{r^2}}}\right) \\ &=-\beta'\frac{\partial }{\partial \rho}\left(\int_{0}^{1}\frac{1}{2\rho^2}\frac{d\xi}{\sqrt{1-\xi}}\right) \\ &\left(\text{here }\xi=\frac{\rho^2}{r^2}\;\right) \\ &=-\beta'\frac{\partial }{\partial \rho}\left(\frac{1}{2\rho^2}\underbrace{ \left. \left( -2\sqrt{1-\xi} \right) \phantom{\frac{1}{1}} \right|_0^1 }_{=2}\right) \\ &=\frac{2\beta'}{\rho^3}=\frac{4kM}{c^2 \rho} \end{align}\]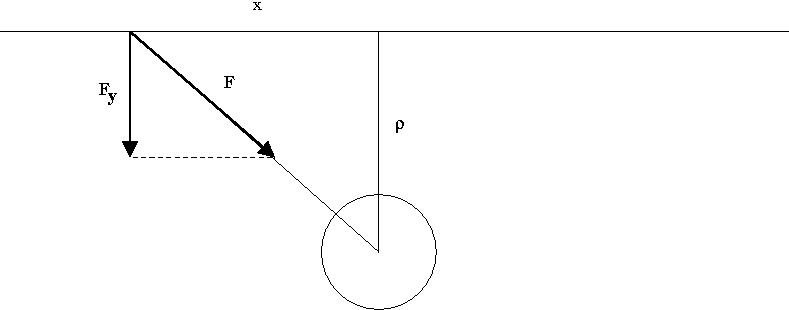 It is straightforward to do a naive special relativistic calculation (for the sake of comparison) according to the idea that a particle moving at light velocity gains a momentum component perpendicular to the original direction, due to Newtonian gravity. The orbit is considered to leading order a straight line. Deflection angle is given by the ratio of the perpendicular momentum component to the original momentum.

\[\begin{align} F&=\frac{k\;E/c^2\;M}{\rho^2+x^2}\\ F_y&=\frac{\rho\;k\;E/c^2\;M}{\left(\rho^2+x^2\right)^{\frac{3}{2}}}\\ \delta \varphi&=\frac{\Delta p}{E/c}=\frac{c}{E}\int_{-\infty}^{\infty} F_y\frac{dx}{c}=\frac{c}{E}\int_{-\infty}^{\infty} \frac{\rho\;k\;E/c^2\;M}{\left(\rho^2+x^2\right)^{\frac{3}{2}}}\frac{dx}{c} \\ &=\frac{kM}{c^2 \rho}\int_{-\infty}^{\infty} \frac{1}{\left(1+\xi^2\right)^{\frac{3}{2}}}d\xi=\frac{kM}{c^2 \rho}\int_{-\pi/2}^{\pi/2} \cos \alpha\; d\alpha \\ &\left(\text{here }\xi=\frac{x}{\rho}={\rm tg}\;\alpha\;\right) \\ &=\frac{2kM}{c^2 \rho} \end{align}\] This is the half of the prediction of general relativity. The reason why we do not get this manner the result of general relativity is that validity of classical approximation two conditions are required:

weak gravitational field
velocities are small compared to light velocity.

In this case the second condition is not satisfied. Gravitational field is actually a tensor field rather than a scalar field, and at large velocities this fact has quantitative consequences.

General relativity predicts \(1.75\) angular second for a light ray passing near the Sun. Actual light deflection was measured first by Eddington in 1919, at the occassion of a total eclipse. The direction of stars near the Sun was compared with their direction half a year later, when the Sun was not around. These first results had large error, yet confirmed general relativity. The currently best result was obtained by radio astonomical methods (Lebach et al., 1995). These have a much better angular resolution and do not require a total eclipse. Results agree with predicton of general relatvity to a relative error of \(8\times 10^{-4}\).

Gravitational red shift

The expression of gravitational red shift may be obtained by elementary considerations, based on energy conservation. A photon makes a distance \(h\) upwards from the surface of Earth. At start it has frequency \(\omega_1\), at arrival \(\omega_2\). The corresponding kinetic energies are \(\hbar\omega_1\) and \(\hbar\omega_2\), respectively. Since its mass is \(\hbar\omega/c^2\) (to first order the change of this may be neglected), the increase of its potential energy is \((\hbar\omega/c^2)gh\), hence energy conservation implies \[\begin{align} \Delta \omega =-\frac{\omega gh}{c^2}\;.\phantom{reds2} \end{align}\] This agrees accidentally with the redshift obtained in general relativity, as calculated before. The effect is very small, the relative chage of frequency is \(2\times 10^{-15}\) on \(22.5\;m\) (this was the level distance applied in the first experiment). Yet this minor change was observed already in 1960 by Pound and Rebka, due to the just discovered Mössbauer effect. (According to this, in solids at low temperature there is an enhanced probability for recoil-free gamma resonances, whose natural line widths are very small, allowing extremely sensitive measurements.) The Pound-Rebka experiment confirmed gravitational red shift to 10% . Pound and Schneider reduced this error to 1% in 1964, then in 1980 Vessot et. al. achieved an accuracy of 0.01% (\(10^{-4}\)) using a hydrogen maser deployed to a satellite.

bene@arpad.elte.hu