- Kérdés: milyen lokális mennyiség jelzi, hogy görbült a téridő?
- Vektor párhuzamos eltolása: a komponensek lokálisan Minkowski téridőben
változatlanok. Tetszőleges téridőben:
$$DA^i=0$$
- Geodetikus ($Du^i=0$) mentén végzett párhuzamos eltolás során
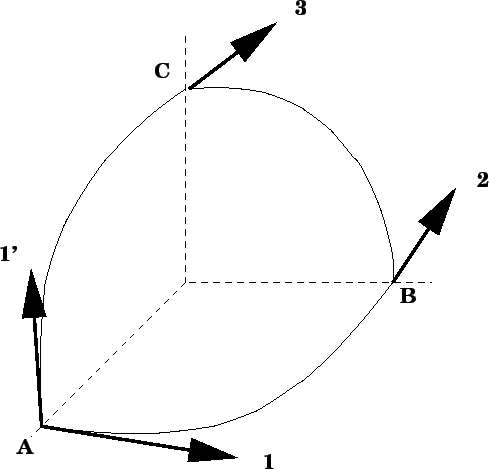
a pálya
érintőjével ($u^i$) bezárt szög állandó.
- Párhuzamos eltolás zárt görbe mentén
Ábra:
Görbült felületen szakaszonként geodetikus zárt görbe mentén végzett párhuzamos eltolás eredménye nem egyezik meg a kiindulási vektorral.
|
|
-
$$
\Delta A_k=\oint \Gamma^i_{\phantom{1}kl}A_i dx^l
$$
$$
\frac{\partial A_i}{\partial x^l}=\Gamma^n_{\phantom{1}il}A_n
$$
- Stokes tétele
-
$$
\Delta A_k=\frac{1}{2}\left[
\frac{\partial \left(\Gamma^i_{\phantom{1}km} A_i\right)}{\partial x^l}-
\frac{\partial \left(\Gamma^i_{\phantom{1}kl} A_i\right)}{\partial x^m}
\right]\Delta f^{lm}
$$
-
$$
\Delta A_k=\frac{1}{2}R^i_{\phantom{1}klm}A_i \Delta f^{lm}
$$
-
$$
R^i_{\phantom{1}klm}=
\frac{\partial \Gamma^i_{\phantom{1}km} }{\partial x^l}
-\frac{\partial \Gamma^i_{\phantom{1}kl} }{\partial x^m}
+\Gamma^i_{\phantom{1}nl}\Gamma^n_{\phantom{1}km}-\Gamma^i_{\phantom{1}nm}\Gamma^n_{\phantom{1}kl}
$$
(levezetés)
-
$$
\Delta A^k=-\frac{1}{2}R^k_{\phantom{1} ilm}A^i \Delta f^{lm}
$$
(levezetés)
-
$$
A_{i;k;l}-A_{i;l;k}=A_m R^m_{\phantom{1}ikl}
$$
(levezetés)
-
$$
A^i_{;k;l}-A^i_{;l;k}=-A^m R^i_{\phantom{1}mkl}
$$
(levezetés)
- A görbületi tenzor tulajdonságai
-
$$
R_{iklm}=g_{in}R^n_{\phantom{1}klm}
=
\frac{1}{2}\left(\frac{\partial^2 g_{im}}{\partial x^k \partial x^l}
+\frac{\partial^2 g_{kl}}{\partial x^i \partial x^m}
-\frac{\partial^2 g_{il}}{\partial x^k \partial x^m}
-\frac{\partial^2 g_{km}}{\partial x^i \partial x^l}
\right)$$
$$
+g_{np}\left(\Gamma^n_{\phantom{1}kl}\Gamma^p_{\phantom{1}im}-\Gamma^n_{\phantom{1}km}\Gamma^p_{\phantom{1}il}\right)
$$
(levezetés)
-
$$
R_{iklm}=-R_{kilm}=-R_{ikml}
$$
-
$$
R_{iklm}=R_{lmik}
$$
-
$$
R_{iklm}+R_{imkl}+R_{ilmk}=0
$$
(levezetés)
- Bianchi-azonosság:
$$
R^n_{\phantom{1}ikl;m}+R^n_{\phantom{1}imk;l}+R^n_{\phantom{1}ilm;k}=0
$$
(bizonyítás)
- Ricci-tenzor:
$$
R_{ik}=g^{lm}R_{limk}=R^m_{\phantom{1}imk}
$$
$$
R_{ik}=R_{ki}
$$
- Invariáns görbület:
$$
R=g^{ik}R_{ik}
$$
- Kétdimenziós eset:
$$
R=\frac{2R_{1212}}{\gamma}
$$
$$
\frac{R}{2}=K=\frac{1}{\rho_1\rho_2}
$$
(levezetés)
- A Bianci-azonosságból indexösszeejtéssel ($i$-t $k$-val, $n$-et $l$-lel)
kapjuk:
$$
0=g^{ik}\left(R^l_{\phantom{1}ikl;m}+R^l_{\phantom{1}imk;l}+R^l_{\phantom{1}ilm;k}\right)=-R_{,m}+2R^l_{\phantom{1}m;l}
$$
vagy
$$R^l_{\phantom{1}m;l}=\frac{1}{2}\frac{\partial R}{\partial x^m}$$
- A görbületi tenzor független komponenseinek száma:
- Kétdimenziós eset: egyetlen független komponens, pl.$R_{1212}$.
- Háromdimenziós eset: $R_{\alpha\beta\gamma\delta}$ első ($\alpha\beta$)és
második ($\gamma\delta$) indexpárjai három-három értéket vehetnek fel, tehát
a független komponensek megegyeznek egy szimmetrikus 3X3-as mátrix
komponenseinek számával, azaz 6-tal. (A ciklikus összeg automatikusan
eltűnik.)
- Négydimenziós eset: $R_{iklm}$ első ($ik$) és második ($lm$) indexpárjai
hat-hat értéket vehetnek fel. Egy 6X6-os szimmetrikus mátrix független
komponenseinek száma 21. A ciklikus összeg csak akkor nem tűnik el
automatikusan, ha mind a négy index különböző, ezért egyetlen további
összefüggést ad a komponensek között. Négy dimenzióban tehát a görbületi tenzor
független komponenseinek száma 20.
- Weil-tenzor:
$$C_{iklm}=R_{iklm}-\frac{1}{2}R_{il}g_{km}+\frac{1}{2}R_{im}g_{kl}+\frac{1}{2}R_{kl}g_{im}-\frac{1}{2}R_{km}g_{il}+\frac{1}{6}R\left(g_{il}g_{km}-g_{im}g_{kl}\right)$$
Rendelkezik a görbületi tenzor minden algebrai szimmetriájával, de bármely
indexpárját összeejtve nullát kapunk (irreducibilis tenzor).
- Petrov-féle kanonikus típusok és a görbületi tenzor (ill. a Weil-tenzor)
invariánsai:
- Tegyük fel, hogy $R_{ik}=0$ (ellenkező esetben vizsgáljuk a Weil-tenzort a
görbületi tenzor helyett).
- A téridő adott pontjában válasszunk olyan koordinátarendszert, melyben a
metrika Minkowski alakú.
- Legyen
$$A_{\alpha\beta}=R_{0\alpha0\beta}\,,\quad
C_{\alpha\beta}=\frac{1}{4}e_{\alpha\gamma\delta}e_{\beta\lambda\mu}R_{\gamma\delta\lambda\mu}\,,\quad
B_{\alpha\beta}=\frac{1}{2}e_{\alpha\gamma\delta}R_{0\beta\gamma\delta}$$
- $A_{\alpha\beta}$ és $C_{\alpha\beta}$ szimmetrikus.
- Mivel $R_{0123}+R_{0312}+R_{0231}=0$, a $B_{\alpha\beta}$ mátrix spurja
eltűnik.
- Az $R_{ik}=0$ feltevés következtében
$$A_{\alpha\alpha}=0\,,\quad B_{\alpha\beta}=B_{\beta\alpha}\,,\quad
A_{\alpha\beta}=-C_{\alpha\beta}$$
- $R_{iklm}$ Lorentz-transzformációi egyenértékűek a
$$D_{\alpha\beta}=A_{\alpha\beta}+iB_{\alpha\beta}$$
szimmetrikus, spurtalan komplex mátrix háromdimenziós komplex forgatásaival.
- A
$$D_{\alpha\beta}n_\beta=\lambda n_\beta$$
sajátértékprobléma megoldásai szerint történik az osztályozás. Ha a
szimmetrikus komplex mátrix
hasonlósági transzformációval diagonalizálható, akkor
három ortogonális sajátvektora van úgy, hogy ezek négyzete nem nulla. Ha a
mátrix nem diagonalizálható, akkor a sajátvektorok száma kevesebb és van
közöttük olyan, melynek négyzete nulla, a hozzátartozó sajátérték pedig
degenerált.
- $$ \lambda^{(1)}+\lambda^{(2)}+\lambda^{(3)}=0$$
- Petrov-I. Három független sajátvektor létezik. Ekkor négy független
invariáns van (a két komplex sajátérték, ha ezek egyenlők, D-típusról beszélünk)
Invariánsok kifejezése a görbületi tenzorral:
$$I_1=\frac{1}{48}\left(R_{iklm}R^{iklm}-iR_{iklm}\tilde R^{iklm}\right)=\frac{1}{3}\left(\lambda^{(1)2}+\lambda^{(2)2}+\lambda^{(1)}\lambda^{(2)}\right)$$
$$I_2=\frac{1}{96}\left(R_{iklm}R^{lmpr}R_{pr}^{\phantom{pr}ik}+iR_{iklm}R^{lmpr}\tilde R_{pr}^{\phantom{pr}ik}\right)=\frac{1}{2}\lambda^{(1)}\lambda^{(2)}\left(\lambda^{(1)}+\lambda^{(2)}\right)$$
Itt
$$\tilde R_{iklm}=\frac{1}{2}E_{ikpr}R^{pr}_{\phantom{ik}lm}$$
a görbületi tenzor duálisa.
- Petrov-II. Két független sajátvektor van, és $\lambda^{(1)}=\lambda^{(2)}$.
Ekkor csak két invariáns létezik:
$$I_1=\lambda^{2}\,,\quad I_2=\lambda^{3}\, \rightarrow \,I_1^3=I_2^2$$
Ha $\lambda^{(1)}=0$, N-típusról beszélünk.
- Petrov-III. Egy független sajátvektor van, és
$\lambda^{(1)}=\lambda^{(2)}=\lambda^{(3)}=0$. A görbületi tenzor nullától
különböző, de mégsem létezik a görbületet jellemző invariáns mennyiség.
