


Next: About this document ...
Általános relativitáselmélet
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
9. Előadás: Az általános relativitáselmélet kísérleti
bizonyítékai
9.1. Ekvivalencia-elv, Eötvös-kísérlet


| Év | Kutató | Pontosság | Módszer |
|
| 500? |
Philoponus[20] |
"small" |
Drop Tower |
| 1585 |
Stevin[19] |
5·10-2 |
Drop Tower |
| 1590? |
Galileo[2] |
2·10-2 |
Pendulum, Drop Tower |
| 1686 |
Newton[3] |
10-3 |
Pendulum |
| 1832 |
Bessel[21] |
2·10-5 |
Pendulum |
| 1910 |
Southerns[22] |
5·10-6 |
Pendulum |
| 1918 |
Zeeman[23] |
3·10-8 |
Torsion Balance |
| 1922 |
Eötvös[24] |
5·10-9 |
Torsion Balance |
| 1923 |
Potter[25] |
3·10-6 |
Pendulum |
| 1935 |
Renner[26] |
2·10-9 |
Torsion Balance |
| 1964 |
Dicke,Roll,Krotkov[27] |
3·10-11 |
Torsion Balance |
| 1972 |
Braginsky,Panov[28] |
10-12 |
Torsion Balance |
| 1976 |
Shapiro, et al.[29] |
10-12 |
Lunar Laser Ranging |
| 1981 |
Keiser,Faller[30] |
4·10-11 |
Fluid Support |
| 1987 |
Niebauer, et al.[31] |
10-10 |
Drop Tower |
| 1989 |
Heckel, et al.[32] |
10-11 |
Torsion Balance |
| 1990 |
Adelberger, et al.[33] |
10-12 |
Torsion Balance |
| 1999 |
Baeßler, et al.[34] |
5·10-13 |
Torsion Balance |
| 2010? |
MiniSTEP[35] |
10-17 |
Earth Orbit |
9.2. Perihélium-elfordulás
$$
\delta \varphi=\frac{6\pi k^2 m^2 M^2}{c^2 J^2}=\frac{6\pi k M}{c^2 a(1-e^2)}
$$
A Merkur perihélium-elfordulásának eredete
| mérték (szögmásodperc/évszázad) |
ok |
| 5025".6 |
viszonyítási irány elmozdulása (földtengely precessziója miatt) |
| 531".4 |
a többi bolygó perturbáló hatása |
| < 0.1 |
a Nap lapultsága |
| 42".98±0".04 |
általános relativitáselmélet |
| 5600".0 |
összesen |
| 5599".7 |
megfigyelt érték |
9.3. Fénysugarak eltérülése gravitációs térben, lencsézés
$$
\delta \varphi=\frac{2r_g}{\rho}=\frac{4kM}{c^2\rho}
$$

 Jelenlegi legjobb érték (Eubanks et. al., 2001): $0.99992\pm 0.00014$
Jelenlegi legjobb érték (Eubanks et. al., 2001): $0.99992\pm 0.00014$
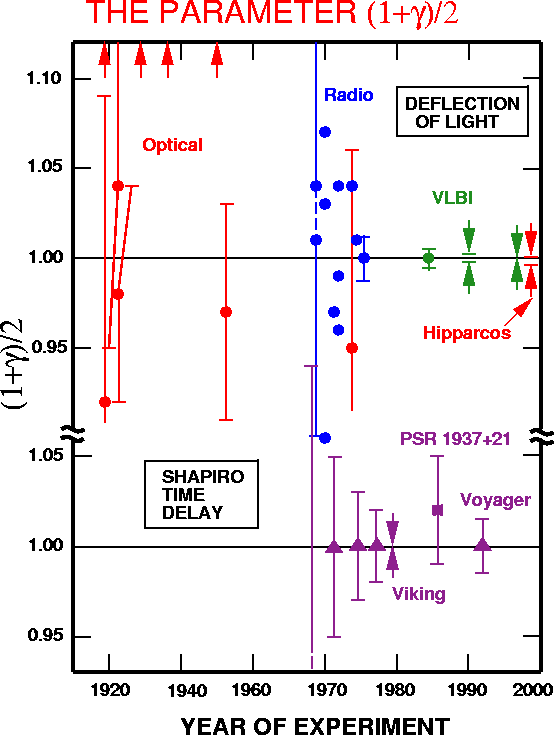

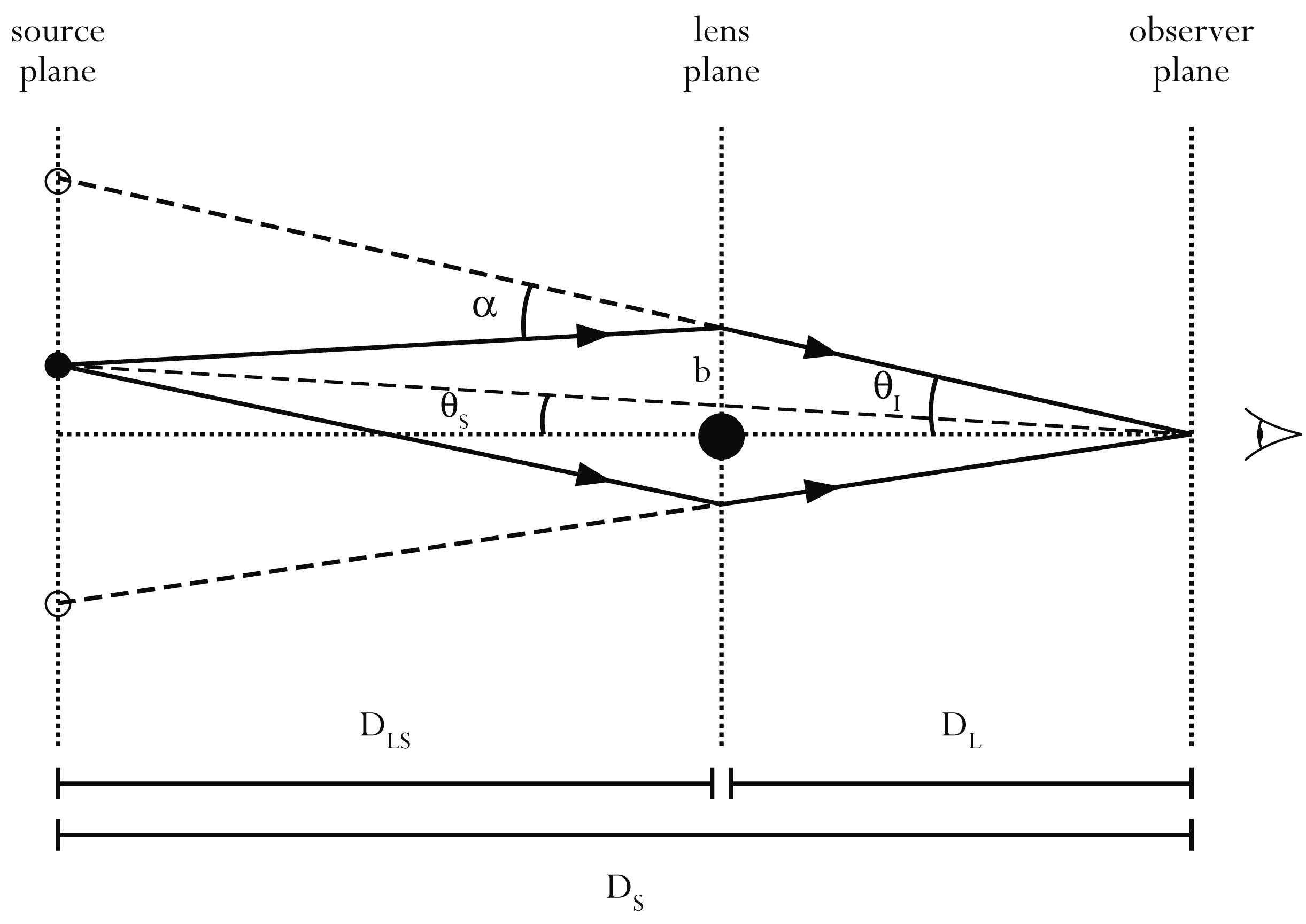
$$\Theta_I=\sqrt{\frac{4kM}{c^2}\frac{D_{LS}}{D_LD_S}}$$
9.4. Gravitációs hullámok, Hulse-Taylor-pulzár
Gyenge gravitációs tér:
$$
g_{ik}=g_{ik}^{(0)}+h_{ik}
$$
$$
g^{ik}=g^{(0) ik}+h^{ik}
$$
$$
g=g^{(0)}(1+h)\quad h=h_i^i
$$
Infinitezimális koordinátatranszformáció ($x^{'i}=x^i+\xi^i$) hatása:
$$
h_{ik}'=h_{ik}-\frac{\partial \xi_i}{\partial x^k}-\frac{\partial \xi_k}{\partial x^i}
$$
Mellékfeltétel:
$$
\frac{\partial \psi_i^k}{\partial x^k}=0\;,\quad
\psi_i^k=h_i^k-\frac{1}{2}\delta_i^k h
$$
Ricci-tenzor:
$$
R_{ik}=\frac{1}{2}\left(\triangle-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)
$$
További mértékszabadság:
$$
\left(\triangle-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\xi^i=0
$$
Vákuumbeli gravitációs hullámok:
$$
\left(\triangle-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)h_i^k=0
$$
$x$ irányú síkhullám:
$$
\left(\frac{\partial^2}{\partial x^2}-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)h_i^k=0
$$
Pozitív irányban terjedő megoldás:
$$
h_i^k=h_i^k(t-x/c)
$$
Mellékfeltételek:
$$
\dot \psi_i^1=\dot \psi_i^0
$$
Alkalmas
$$
x^{'i}=x^i+\xi^i(t-x/c)
$$
koordinátatranszformációval nullává tesszük a
$$\psi_1^0\;,\;\psi_2^0\;,\;\psi_3^0\;,\;\psi_2^2+\psi_3^3$$
komponenseket.
Két független mennyiség marad: $h_{23}=h_{32}$
és $h_{22}=-h_{33}$. $\Rightarrow$ Két transzverzális polarizáció.
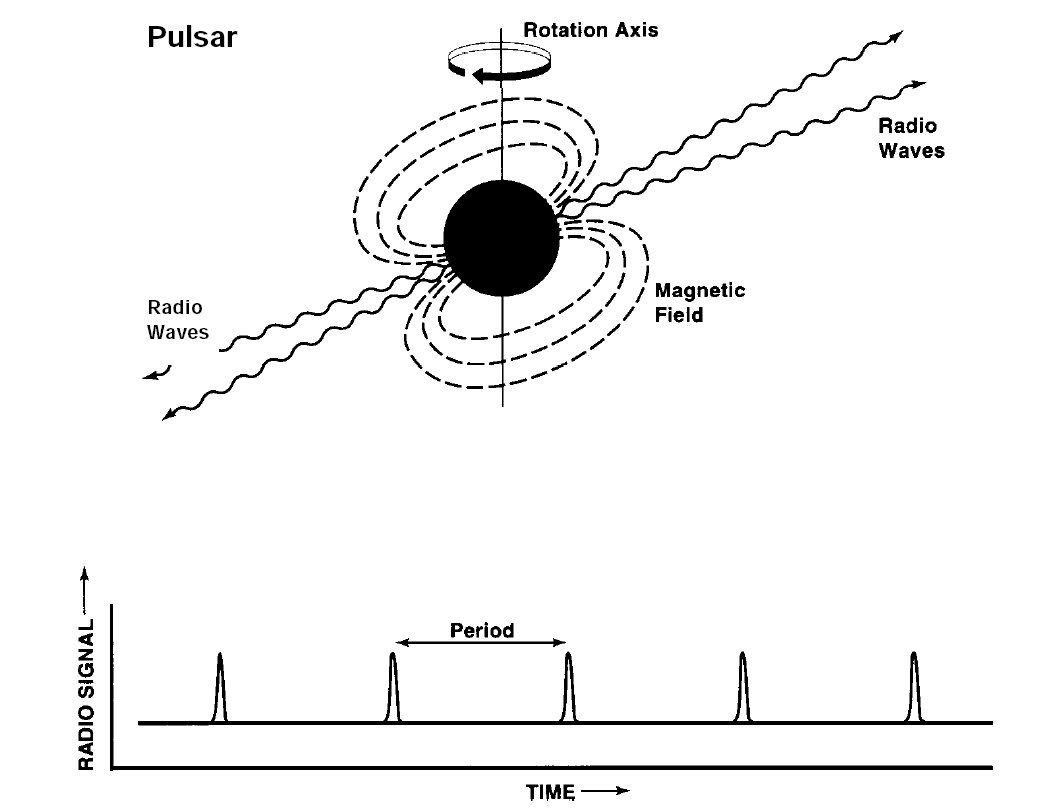



9.5. Gravitációs vöröseltolódás, Pound-Rebka-kísérlet
$$
\Delta \omega=\frac{g(h_1-h_2)}{c^2}\omega
$$
1961, 1%-os pontosság
1976, hidrogén mézer 10 000 km magasba fellőve: 0,007% pontosság
9.6. Gravitációs idődilatáció, Hafele-Keating-kísérlet
1971, J. C. Hafele és Richard E. Keating: repülőgépen szállított cézium
atomórák késése
GPS rendszerben $38\;\mu s$/nap késés.
9.7. A Lense-Thirring-effektus és a Gravity Probe B kísérlet
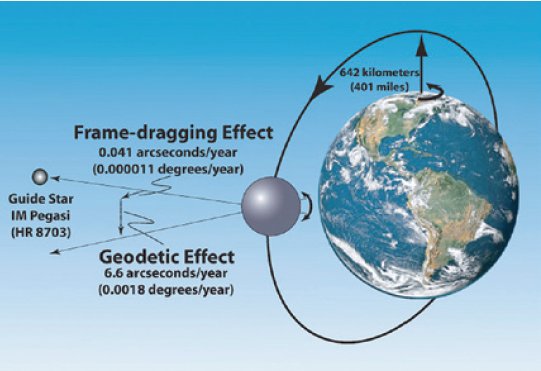







Next: About this document ...
Gyula Bene
2002-11-22





 Jelenlegi legjobb érték (Eubanks et. al., 2001): $0.99992\pm 0.00014$
Jelenlegi legjobb érték (Eubanks et. al., 2001): $0.99992\pm 0.00014$











