Hidrodinamika

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
11. Előadás

11.1. Ismétlés

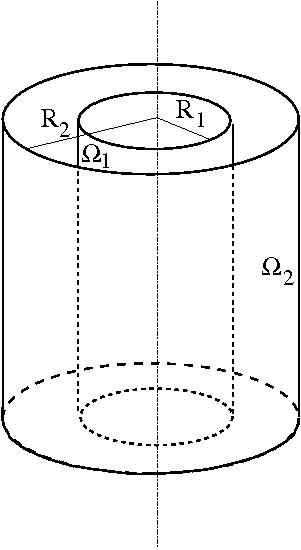
11.2. Áramlás koncentrikus, forgó hengerek közt (Couette-Taylor-áramlás). Egzakt megoldás és stabilitásvizsgálat

• A Navier-Stokes-egyenletek hengerkoordinátákban: $$ \begin{eqnarray} \frac{\partial v_r}{\partial t}&+&v_r\frac{\partial v_r}{\partial r}+\frac{v_\varphi}{r}\frac{\partial v_r}{\partial \varphi}+v_z\frac{\partial v_r}{\partial z}-\frac{v_\varphi^2}{r}=\\ &=&-\frac{1}{\rho}\frac{\partial p}{\partial r}+\nu\left(\frac{\partial^2 v_r}{\partial r^2}+\frac{1}{r^2}\frac{\partial^2 v_r}{\partial \varphi^2}+\frac{\partial^2 v_r}{\partial z^2}+\frac{1}{r}\frac{\partial v_r}{\partial r}-\frac{2}{r^2}\frac{\partial v_\varphi}{\partial \varphi}-\frac{v_r}{r^2}\right)\\ \frac{\partial v_\varphi}{\partial t}&+&v_r\frac{\partial v_\varphi}{\partial r}+\frac{v_\varphi}{r}\frac{\partial v_\varphi}{\partial \varphi}+v_z\frac{\partial v_\varphi}{\partial z}+\frac{v_r v_\varphi}{r}=\\ &=&-\frac{1}{\rho r}\frac{\partial p}{\partial \varphi}+\nu\left(\frac{\partial^2 v_\varphi}{\partial r^2}+\frac{1}{r^2}\frac{\partial^2 v_\varphi}{\partial \varphi^2}+\frac{\partial^2 v_\varphi}{\partial z^2}+\frac{1}{r}\frac{\partial v_\varphi}{\partial r}+\frac{2}{r^2}\frac{\partial v_r}{\partial \varphi}-\frac{v_\varphi}{r^2}\right)\\ \frac{\partial v_z}{\partial t}&+&v_r\frac{\partial v_z}{\partial r}+\frac{v_\varphi}{r}\frac{\partial v_z}{\partial \varphi}+v_z\frac{\partial v_z}{\partial z}=\\ &=&-\frac{1}{\rho}\frac{\partial p}{\partial z}+\nu\left(\frac{\partial^2 v_z}{\partial r^2}+\frac{1}{r^2}\frac{\partial^2 v_z}{\partial \varphi^2}+\frac{\partial^2 v_z}{\partial z^2}+\frac{1}{r}\frac{\partial v_z}{\partial r}\right)\\ \frac{\partial v_r}{\partial r}&+&\frac{1}{r}\frac{\partial v_\varphi}{\partial \varphi}+\frac{\partial v_z}{\partial z}+\frac{v_r}{r}=0 \end{eqnarray} $$
• Feltevés: $$v_r=v_z=0\;,\quad v_\varphi=v_\varphi(r)\;,\quad p=p(r)$$ Ekkor a két utolsó egyenlet azonosan teljesül. A megmaradt két egyenletből: $$ \begin{eqnarray} \frac{\partial p}{\partial r}&=&\rho\frac{v_\varphi^2}{r}\\ \frac{\partial^2 v_\varphi}{\partial r^2}&+&\frac{1}{r}\frac{\partial v_\varphi}{\partial r}-\frac{v_\varphi}{r^2}=0 \end{eqnarray} $$
• Keressük a megoldás hatványfüggvényként! $$ v_\varphi=a\;r^n$$ A második egyenletből $$n(n-1)\;a\;r^{n-2}+na\;r^{n-2}-a\;r^{n-2}=0\;,$$ azaz $$n^2-1=0$$ Tehát $n=\pm 1$, így az általános megoldás $$v_\varphi=a\;r+\frac{b}{r}$$ Mivel $v_\varphi(R_1)=R_1\Omega_1$ és $v_\varphi(R_2)=R_2\Omega_2$ a határfeltételek, $$v_\varphi=\frac{R_2^2\Omega_2-R_1^2\Omega_1}{R_2^2-R_1^2}\;r-\frac{R_2^2R_1^2(\Omega_2-\Omega_1)}{R_2^2-R_1^2}\frac{1}{r}$$ a határfeltételeket teljesítő egzakt megoldás.
• Stabilitásvizsgálat nagy Reynolds-számok esetén:
  Ekkor a nyíróerők a folyadék belsejében elhanyagolhatók, így az impulzusmomentum megmarad.
  $J_0$ impulzusmomentumú $m$ tömegű folyadékelemet a tengelytől $r_0$ távolságban $$F_0=\frac{J_0^2}{mr_0^3}$$ centripetális erő tart körpályán. Ha a folyadékelem elmozdul egyensúlyi helyzetéből és a tengelytől $r>r_0$ távolságra kerül, ott $$F=\frac{J^2}{mr^3}$$ centripetális erő hat rá, viszont $$F_0'=\frac{J_0^2}{mr^3}$$ erő tartaná egyensúlyban. Az eredeti egyensúlyi helyzetbe nyilván akkor tér vissza, ha $$F>F_0'\;,\quad\text{azaz}\;J^2>J_0^2$$ Másképp kifejezve $$J\frac{dJ}{dr}>0$$ az egyensúly feltétele.
  A fenti egzakt megoldást behelyettesítve az egyensúly feltétele tehát $$\left(R_2^2\Omega_2-R_1^2\Omega_1\right)\dot{\varphi}>0$$ ahol $$\dot{\varphi}=\frac{v_\varphi}{r}=\frac{R_2^2\Omega_2-R_1^2\Omega_1}{R_2^2-R_1^2}-\frac{R_2^2R_1^2(\Omega_2-\Omega_1)}{R_2^2-R_1^2}\frac{1}{r^2}$$ $r$ függvényében monoton változik $\Omega_1$-től $\Omega_2$-ig.
• Kis Reynolds-számok esetén az áramlás mindig stabil
• Áramlási kép nagyobb Reynolds-számok esetén:
  
  
  
  
  
  
  
  
  
  
  
  
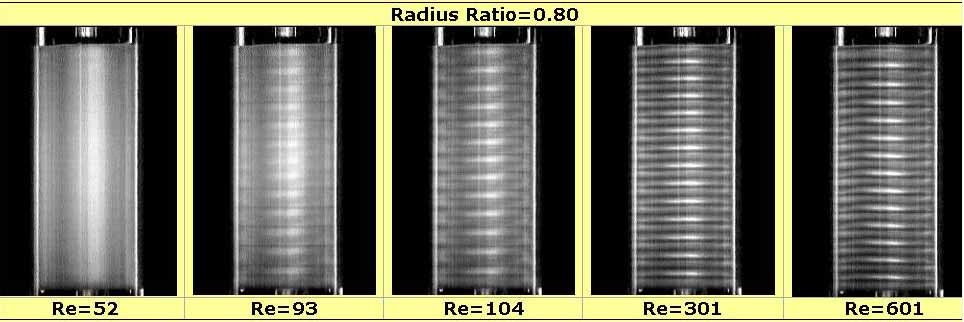
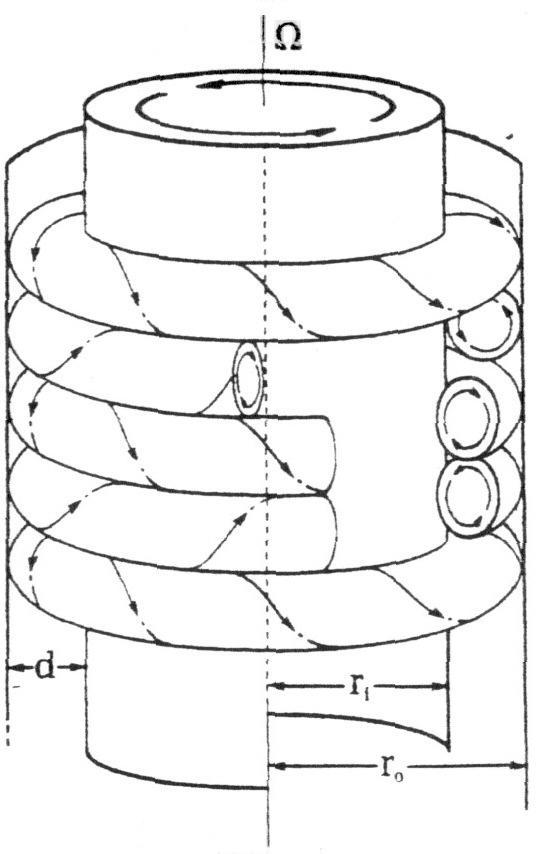
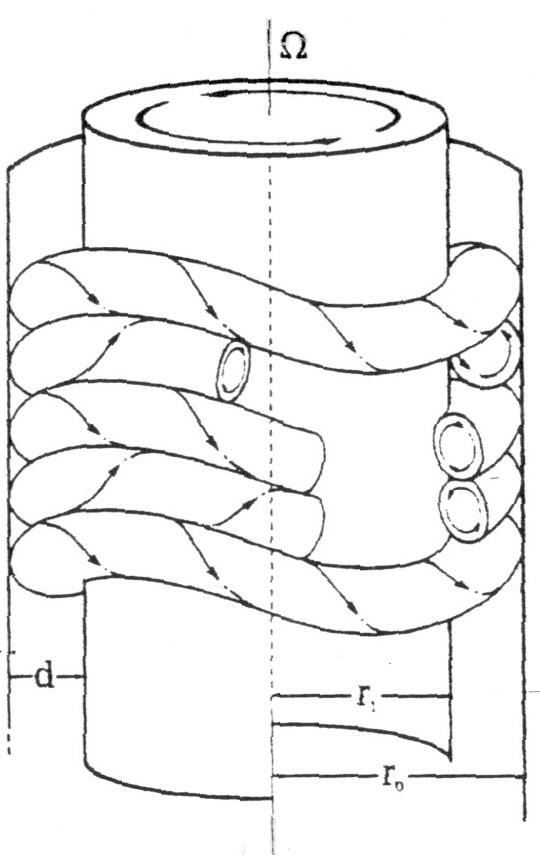
  Re=177__________________________Re=506__________________________Re=3027_________________________Re=8072
  

11.3. Stabilitásvizsgálat általában. A turbulencia kialakulása.

• Lineáris stabilitásvizsgálat.
  Legyen ${\bf v}_0$ és $p_0$ a Navier-Stokes-egyenletek adott határfeltételt teljesítő egzakt megoldása. Adjunk ehhez kis perturbációt: $${\bf v}={\bf v}_0+{\bf v}_1\;,\quad p=p_0+p_1$$ A kis perturbációs tagok szerint lineáris rendben kapjuk: $$ \begin{eqnarray} \frac{\partial {\bf v}_1}{\partial t}+({\bf v}_1\cdot{\bf \nabla}){\bf v}_0+({\bf v}_0\cdot{\bf \nabla}){\bf v}_1&=&-\frac{{\bf \nabla} p_1}{\rho}+\nu\triangle {\bf v}_1\\ {\bf \nabla}\cdot{\bf v}_1&=&0 \end{eqnarray} $$ A határfeltételek ugyanazok ${\bf v}_1$-re, mint ${\bf v}_0$-ra.
  • Ha az alapmegoldás stacionárius, akkor ${\bf v}_1={\bf u}({\bf r})e^{i\omega t}$ alakú megoldások léteznek. A stabilitás feltétele, hogy $\omega$ képzetes része semelyik módusra ne legyen negatív. Instabilitás esetén a perturbáció növekszik, a nemlineáris tagok pedig stabilizálják az eredetileg instabil módust, periodikus mozgás alakul ki.
  • Ha az alapmegoldás periodikus, ${\bf v}_1={\bf u}({\bf r},t)e^{i\omega t}$, ahol ${\bf u}({\bf r},t)$ az alapmegoldás körfrekvenciájával periodikus. Az alapmegoldás körfrekvenciája és $\omega$ aránya általában irracionális (kváziperiodikusság). Instabilitás esetén a perturbáció növekszik, a nemlineáris tagok pedig stabilizálják az eredetileg instabil módust, kváziperiodikus mozgás alakul ki.
  • Ha az alapmegoldás kváziperiodikus, ${\bf v}_1$-ben ismét újabb frekvencia jelenik meg, a megoldás azonban instabilitás esetén a perturbáció növekedtével nem stabilizálódik, hanem tipikusan kaotikussá válik.
  • Nagy Reynolds-számok esetén a mozgás jellegzetes kavargó, aperiodikus, véletlenszerű: turbulens. A turbulencia kvantitatív elmélete nincs kidolgozva.

















• Henger körüli áramlás:
  
  Re=9.6
  
  Re=26
  
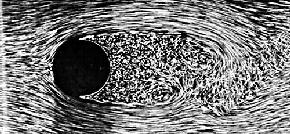
  Re=2000
  
  Re=10000
  
  
  
  
  
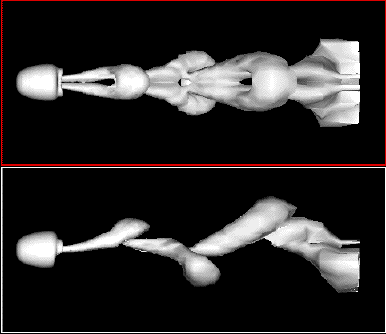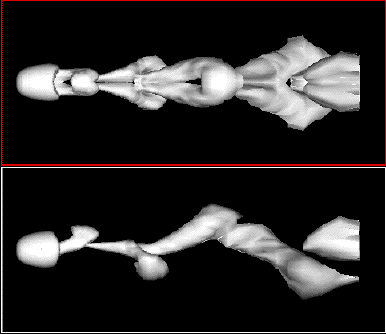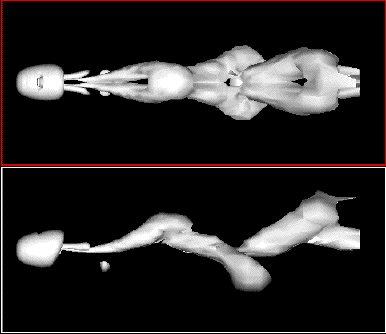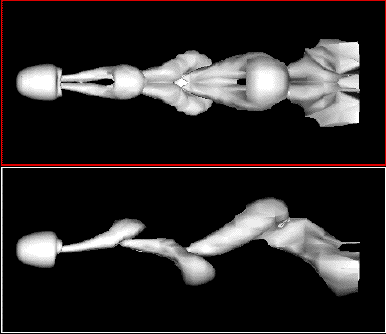
  Örvények leválása gömbről, szimuláció, Re=300
  
• Lamináris vs. turbulens áramlás
  
  
  
  
  
  
  
  
  

11.4. A kifejlett turbulencia. Hasonlósági megfontolások. Lokális turbulencia.
Tömegegységre eső energiadisszipáció időegység alatt: $\epsilon$
Legnagyobb hosszskála: $l$ $$v_\lambda\approx (\epsilon\lambda)^{1/3}$$
Viszkózus hosszskála: $$\lambda_0\approx \frac{l}{\rm Re^{3/4}}\approx \left(\frac{\nu^3}{\epsilon}\right)^{1/4}$$

11.5. Lamináris árnyékzóna.
Áramlásba helyezett test mögött $${\bf v}={\bf U}+{\bf v}'\;.$$ A testre ható erő: $${\bf F}=-\rho U \int_{\begin{array}{l}\text{a test mögött}\\\text{az árnyékzóna}\\\text{keresztmetszetére}\end{array}} {\bf v}'dydz \quad ({\bf U} \;\text{x irányú})$$
Az árnyékzónán belül a Navier-Stokes-egyenlet $\triangle \bf v$ tagja dominál, azon kívül viszont $({\bf \nabla}\cdot {\bf v})\bf v$. Az árnyékzóna határa a két tag egyenlőségéből becsülhető: $$U\frac{u}{x}\approx\nu \frac{u}{y^2}$$ azaz $$y\approx \left(\frac{\nu x}{U}\right)^{1/2}\;.$$ Másrészt $$F_x\approx \rho U u y^2\;,$$ amiből $$u\approx \frac{F_x}{\rho \nu x}$$ a sebesség megváltozása az árnyékzónán belül.

11.6. Turbulens árnyékzóna.
Ezúttal is $$F_x\approx \rho U u y^2\;,$$ de most $$\frac{y}{x}=\frac{u}{U}$$ közelítés használható az árnyékzóna határaira, ugyanis $v_y\approx u$, $v_x\approx U$, a viszkozitás pedig nem játszik szerepet. Ezzel $$y\approx \left(\frac{F_x x}{\rho U^2}\right)^{1/3}\;,\quad u\approx \left(\frac{F_xU}{\rho x^2}\right)^{1/3}$$ $${\rm Re}=\frac{uy}{\nu}\approx\frac{1}{\nu}\left(\frac{F_x^2}{\rho^2 Ux}\right)^{1/3}$$ A Reynolds-szám a testtől mért távolsággal csökken $\Rightarrow$ az árnyékzóna elég távol laminárissá válik.

11.7. Lamináris határréteg. Leszakadási jelenség.

• Prandtl-féle határréteg-egyenletek: $$v_x\frac{\partial v_x}{\partial x}+v_y\frac{\partial v_x}{\partial y}-\nu\frac{\partial^2 v_x}{\partial y^2}=-\frac{1}{\rho}\frac{dp}{dx}=U\frac{dU}{dx}\;,\quad \frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}=0$$ Dimenziótlanítás: $$x=l x'\;,\quad y=\frac{ly'}{\sqrt{\rm Re}}\;,\quad v_x=U_0 v_x'\;,\quad v_y'=\frac{U_0 v_y'}{\sqrt{\rm Re}}\;,\quad \text{ahol}\;{\rm Re}=\frac{U_0 l}{\nu}$$ $$v_x'\frac{\partial v_x'}{\partial x'}+v_y'\frac{\partial v_x'}{\partial y'}-\frac{\partial^2 v_x'}{\partial y'^2}=U'\frac{dU'}{dx'}\;,\quad \frac{\partial v_x'}{\partial x'}+\frac{\partial v_y'}{\partial y'}=0$$
• Leszakadás feltétele: $$\frac{\partial v_x}{\partial y}=0$$

11.8. Logaritmikus sebességprofil. Turbulens áramlás csövekben.

• Síkfelülettel párhuzamos átlagsebességű turbulens áramlást vizsgálunk. A felületegységre ható súrlódási erő: $\sigma$
  Karakterisztikus sebesség: $$v^*=\sqrt{\frac{\sigma}{\rho}}$$
• Viszkózus alhéj: $$y_0\approx \frac{\nu}{v^*}\;,\quad u=\frac{\sigma}{\rho \nu}y$$
• Logaritmikus sebességprofil:
  Dimenzionális okokból $$\frac{du}{dy}=\frac{1}{b}\frac{v^*}{y}\quad(b\;\text{dimenziótlan állandó})\;,$$ így ($u(y_0)=v^*$ határfeltétellel) $$u=\frac{v^*}{b}\ln\frac{yv^*}{\nu}\;,\quad\text{pontosabban: }\;\;u=v^*\left(2.4\ln\frac{yv^*}{\nu}+5.84\right)$$
• Turbulens áramlás csövekben:
  A logaritmikus sebességprofil felhasználásával $y=a$ esetén ($a$ a cső sugara), és mert most $\sigma 2\pi a l=\Delta p \pi a^2$: $$U=\sqrt{\frac{a\Delta p}{2b^2\rho l}}\ln\left(\frac{a}{\nu}\sqrt{\frac{a\Delta p}{2\rho l}}\right)$$
• Csőellenállási együttható: $$\lambda=\frac{\frac{\Delta p}{l}2a}{\frac{1}{2}\rho U^2}$$ Lamináris áramlás esetén: $$\lambda=\frac{64}{\rm Re}$$ Turbulens áramlás esetén (a logaritmikus sebességprofil pontosabb empirikus változatával): $$\frac{1}{\sqrt{\lambda}}=0.85\ln({\rm Re}\sqrt{\lambda})-0.55$$

11.9. Turbulens határréteg. Ellenállási válság. $$U=\frac{v_*}{b}\ln\frac{v_*\delta}{\nu}$$ $$\delta \sim \frac{v_*x}{U}$$ $$F=\frac{1}{2}C_D\rho U^2 A$$

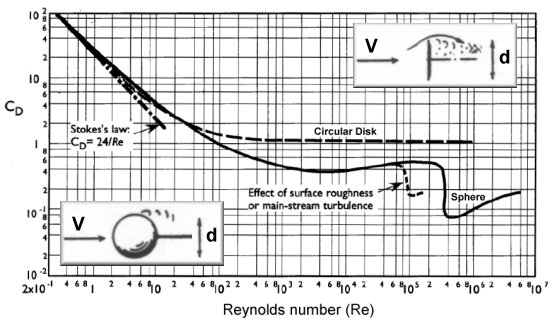
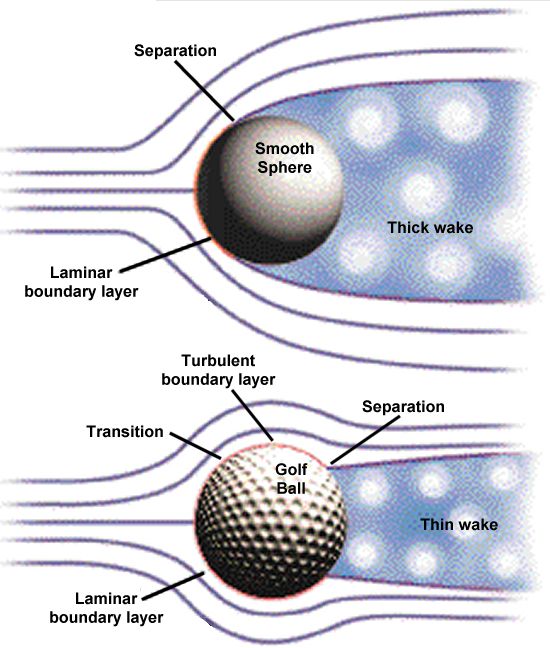
11.10. Szárnyakra ható felhajtóerő.

Áramvonalas szárny