- tömegerők (a közeg minden részében hatnak, kis folyadékrész esetén a tömeggel arányosak): $$d{\bf F}=\rho {\bf f}dV$$ Itt ${\bf f}$ az erősűrűség. Pl. gravitációs térben ${\bf f}={\bf g}$, ahol ${\bf g}$ a nehézségi gyorsulás.
-
felületi erők (a szomszédos folyadékrészek között ható rövid hatótávolságú erők, pl. van der Waals-erők, eredetük: elektrosztatikus + kicserélődési kölcsönhatás a Pauli-elvnek megfelelően):
-
Arányosak a felülettel.
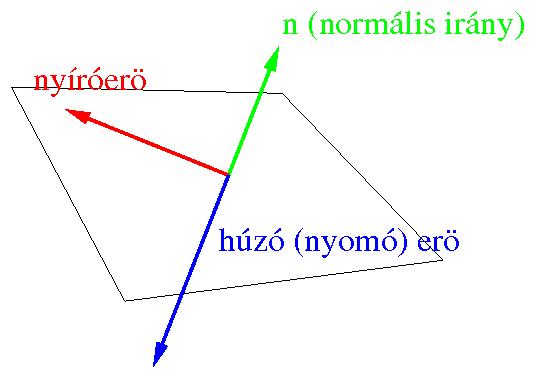
- Húzó és nyomóerők: a felület normálisának irányába mutatnak
- Nyíróerők: a felület normálisára merőleges irányba mutatnak
-
Általában:
$$d{\bf F}={\cal \sigma}{\bf n}dA$$
Itt ${\cal \sigma}$ a feszültségtenzor
Mátrixjelöléssel: $$\left(\begin{array}{c}F_x\\F_y\\F_z\end{array}\right)=\left(\begin{array}{ccc}\sigma_{xx}&\sigma_{xy}&\sigma_{xz}\\\sigma_{yx}&\sigma_{yy}&\sigma_{yz}\\\sigma_{zx}&\sigma_{zy}&\sigma_{zz}\end{array}\right)\left(\begin{array}{c}n_x\\n_y\\n_z\end{array}\right)dA$$
azaz
$\begin{eqnarray} F_x&=&\sigma_{xx}n_x dA+\sigma_{xy}n_y dA+\sigma_{xz}n_z dA\\ F_y&=&\sigma_{yx}n_x dA+\sigma_{yy}n_y dA+\sigma_{yz}n_z dA\\ F_z&=&\sigma_{zx}n_x dA+\sigma_{zy}n_y dA+\sigma_{zz}n_z dA \end{eqnarray}$
Eszerint pl. $\sigma_{zy}$ az $y$ irányba mutató normálisú egységnyi felületelemre ható erő $z$ komponense. - Nyugvó folyadékban ill. gázban nyíróerők nem lépnek fel (Pascal törvénye). $$\left(\begin{array}{ccc}\sigma_{xx}&\sigma_{xy}&\sigma_{xz}\\\sigma_{yx}&\sigma_{yy}&\sigma_{yz}\\\sigma_{zx}&\sigma_{zy}&\sigma_{zz}\end{array}\right) =\left(\begin{array}{ccc}-p&0&0\\0&-p&0\\0&0&-p\end{array}\right)$$
- Áramlás közben valódi folyadékban fellépnek nyíróerők. Oka: belső súrlódás.
- Ideális folyadék: belső súrlódás elhanyagolható, áramlás közben sem lépnek fel benne nyíróerők.
-
Arányosak a felülettel.
- Tetszőleges térfogatra az eredő erő zérus: $$\int \rho {\bf f} dV - \oint p dA =0$$
- Differenciális alak:
x komponens: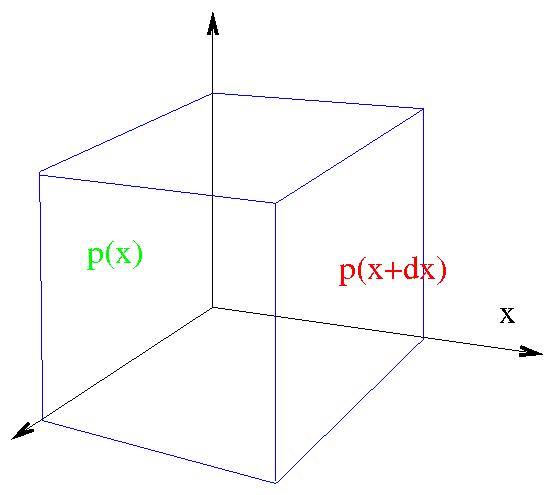 $$\rho f_x \Delta x \Delta y \Delta z -\left(p(x+\Delta
x)-p(x)\right)\Delta y \Delta z=0$$
$$\rho f_x-\frac{\partial p}{\partial x}=0$$
$$\rho f_x \Delta x \Delta y \Delta z -\left(p(x+\Delta
x)-p(x)\right)\Delta y \Delta z=0$$
$$\rho f_x-\frac{\partial p}{\partial x}=0$$
- Vektoralakban: $$\rho {\bf f}-grad\; p=0$$ $$\rho {\bf f}-{\bf \nabla} p=0$$ $${\bf f}-\frac{1}{\rho}{\bf \nabla} p=0$$
A hidrosztatikában ${\bf v}({\bf r},t)=0$. A fenti egyenlet kapcsolat $\rho({\bf r})$ és $p({\bf r})$ között. Ehhez jön még az állapotegyenlet.
- Konzervatív tömegerő: $${\bf f} = -{\bf \nabla} U \;\rightarrow\; \rho {\bf \nabla} U+{\bf \nabla} p = 0$$ Az ekvipotenciális felületek és az izobárok egybeesnek.
- Barotróp folyadék:
$$\rho=\rho(p)$$
pl. összenyomhatatlan folyadék, izoterm folyadék, adiabatikus
folyadék.
$$\frac{p}{\rho}=\frac{R}{M}T$$
$$\frac{p}{\rho^\kappa}=const.$$
Az egyensúlyi egyenletet integrálva: $$U+\int_{p_0}^{p}\frac{dp'}{\rho(p')}=const.$$ nyomásfüggvény: $$P(p)=\int_{p_0}^{p}\frac{dp'}{\rho(p')}$$
Egyensúlyban tehát $U+P=const.$
ha a $z$-tengely ${\bf g}$-vel párhuzamos. Következmény: $\rho$, $p$, $T$ csak $z$-től függ.
- Összenyomhatatlan folyadék: $$\rho_0 g z+p=p_0$$ $p$, $T$ lineáris függvénye a magasságnak.
- Barométeres magasságformula izotermikus ideális gázra: $$P(p)=\int_{p_0}^{p}\frac{dp'}{p'}\frac{RT_0}{M}=\frac{RT_0}{M}\ln \frac{p}{p_0}$$ $$P+U=const.$$ $$p=p_0\;\exp \left(-\frac{Mg}{RT_0}z\right)$$
- Adiabatikus ideális gáz: $$\rho=\rho_0 \left(\frac{p}{p_0}\right)^{1/\kappa}$$ $$\int_{p_0}^{p}\frac{dp'}{\rho_0(p'/p_0)^{1/\kappa}}=\frac{p_0^{1/\kappa}}{\rho_0}\frac{\kappa}{\kappa-1}\left(p^{\frac{\kappa-1}{\kappa}}-p_0^{\frac{\kappa-1}{\kappa}}\right)=-gz$$ $$p=p_0\left(1-\frac{\kappa-1}{\kappa}\frac{\rho_0}{p_0}gz\right)^{\frac{\kappa}{\kappa-1}}$$ $\kappa\rightarrow 1$-re $$p=p_0{\rm e}^{-\frac{\rho_0}{p_0}gz}$$
- Ismert hőmérsékleteloszlású ideális gáz:
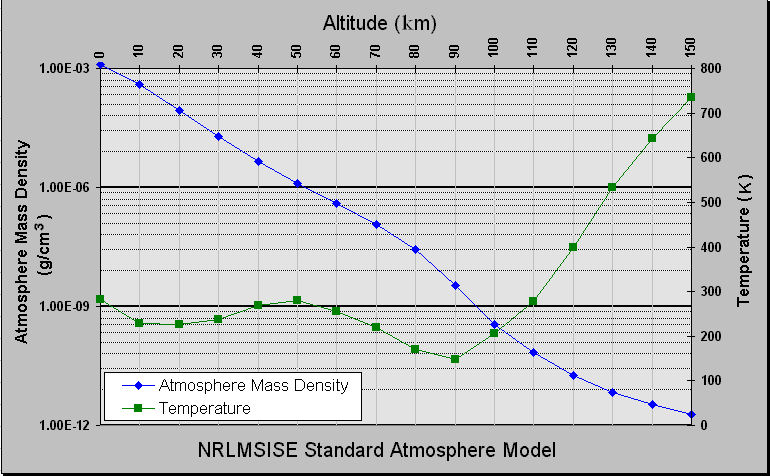 $$\frac{dp}{dz}=-\rho g = -\frac{Mg}{RT(z)}p$$
$$\frac{dp}{p}= -\frac{Mg}{RT(z)}dz$$
$$\ln \frac{p}{p_0}=-\frac{Mg}{R}\int_{z_0=0}^z\frac{dz'}{T(z')}$$
$$\frac{dp}{dz}=-\rho g = -\frac{Mg}{RT(z)}p$$
$$\frac{dp}{p}= -\frac{Mg}{RT(z)}dz$$
$$\ln \frac{p}{p_0}=-\frac{Mg}{R}\int_{z_0=0}^z\frac{dz'}{T(z')}$$
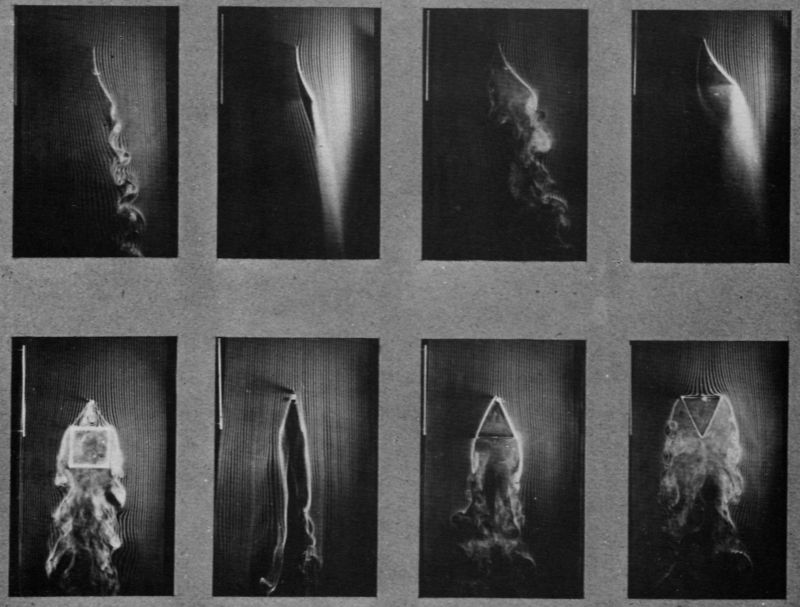
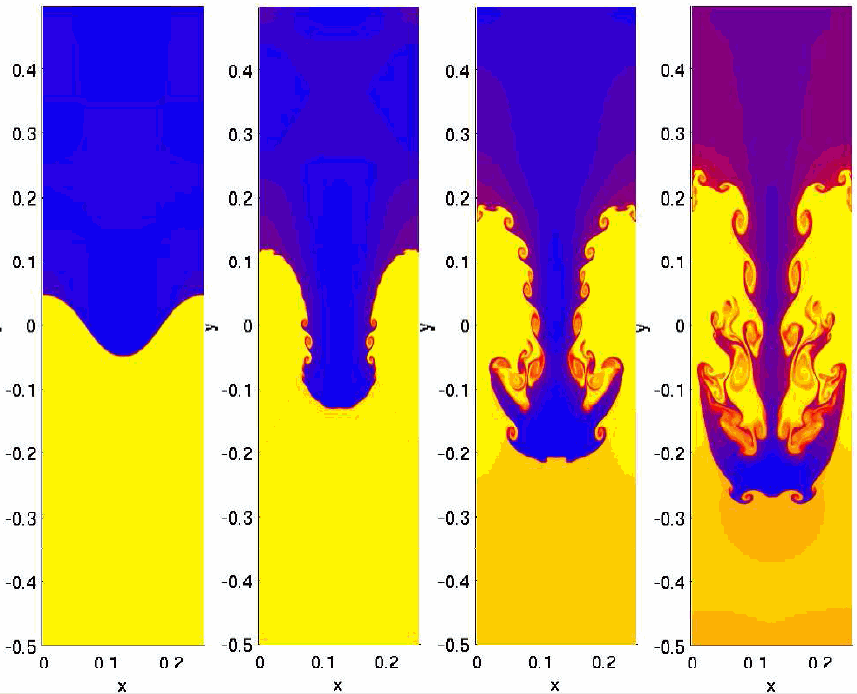







 Légy
Légy