Hővezetés gömbhéjon

Szalai Dávid

G1UMOW

2018.05.21

Feladat

Oldja meg az időfüggő hővezetés egyenletét gömbhéjra a következő feltételek mellett:

  • minden pontban időfüggő forrás van jelen, melynek forráserőssége:

    $max(0, cos\theta cos\theta_0 + sin\theta sin\theta_0 cos(\phi − \omega t))$

  • minden pontban az abszolút hőmérséklet negyedik hatvanyával arányos nyelő van jelen (sugárzási hőveszteség)

  • kezdetben a hőmérséklet a gömbhéj minden pontjában azonos

Hővezetés egyenlete

A feladat elvégzéséhez először meghatározom azt a differenciál egyenletet, melynek megoldásaként mekapható a hőterjedés egy gömbhéjon. Az általános hővezetési egynelet [Heat Equaton] alapján a következő:

\begin{equation} \frac{\partial u}{\partial t} - \alpha \nabla^2 u = 0, \end{equation}

ahol, $\alpha = \frac{k}{\rho c_p}$ a hővezetési együttható, $\rho$ a sűrűség, $c_p$ a hőkapacitás, $k$ pedig a termikus vezetőképesség. Mivel gömb felületen dolgozunk célszerű áttérni polárkordinátákra ($x,y,z \rightarrow r, \theta, \phi$), ekkor [Polar Coordinates] alapján $\nabla^2$ (Laplace) a következő alkot ölti:

\begin{equation} \nabla^2 u = \frac{\partial ^2u}{r^2} + \frac{1}{r^2}\frac{\partial ^2u}{\partial \theta^2} +\frac{1}{r^2}\frac{1}{sin^2\theta} \frac{\partial ^2u}{\partial \phi^2} + \frac{2}{r}\frac{\partial u}{\partial r} + \frac{1}{r^2}\frac{1}{tan\theta}\frac{\partial u}{\partial \theta} \end{equation}

Az egyszerűség kevért $r = 1$ értéket választom, továbbá a gömbhéj vastagságát elhanyagolhatóan kicsinek veszem, így az $r$ szerinti deriváltak kiesnek az egyenletből ($\frac{\partial u}{\partial r} \approx 0$). Ez alapján a hővezetés egyenlete a következőképp néz ki:

\begin{equation} \frac{\partial u}{\partial t} = \alpha \left[ \frac{\partial ^2u}{\partial \theta^2} +\frac{1}{sin^2\theta} \frac{\partial ^2u}{\partial \phi^2} + \frac{1}{tan\theta}\frac{\partial u}{\partial \theta} \right] \end{equation}

Esetünkben a hőmérsékletre ($T$) szeretném megoldani az egyenletet, amihez hozzáadódik az időfőggő hőforrás (Q), illetve a hőveszteség. Így a megoldandi kívánt differenciál egyenlet a következő: \begin{gather} Q = max(0, cos\theta cos\theta_0 + sin\theta sin\theta_0 cos(\phi − \omega t)) \ \frac{\partial T}{\partial t} = \alpha \left[ \frac{\partial ^2T}{\partial \theta^2} +\frac{1}{sin^2\theta} \frac{\partial ^2T}{\partial \phi^2} + \frac{1}{tan\theta}\frac{\partial T}{\partial \theta} \right] + bQ - \sigma T^4 \end{gather} Az egyenletben szereplő $\omega$ az időföggő hőforrás frekvenciája, $\sigma$ a hőveszteségi együttható, melynek értékét a szimuláció során a Stefan-Boltzmann állandó értékének állítottam be, azza $\sigma = 5.672 \cdot 10^{-8} \frac{W}{m^2 K^4}$. Bevezettem továbbá még egy $b$ paramétert, ami a hőforrás erősségét hivatott szabályozni, hogy kellőképpen tudjam kompenzálni a hőveszteséget.

A differenciál egyenlet numerikus megoldás

A numerikus megoldás főbb lépéseit a következőkben ismertetem, a megírt c++ kód pedig a csatolt main.cpp file-ban taláható. A parciális differenciál egyenlet megoldásához [ FTCS_scheme] alpján az FTCS (Forward-Time Central-Space) módszert használtam, ami hővezetési egyenlet és hasonló parabolikus parciális differenciál egyenletek megoldásához szoktak használni. Az FTCS mószer térben a középpontól való távolságon alapul, míg időben egy explicit Euler módszer.

A hőterjedés vizsgálatához a gömb felszínét diszkrét területegységekre bontottam, az alábbi térhálós szerkezetnek megfelelően: Sphere

Gömb felosztása kis területegységekre.

A gömbfelület kiterített hálóján lévő négyzetrácsokat $i, j$ indexekkel fogom jelülni. Ezen négyzetrácsok $\theta$, $\phi$ egységekben vannak felbontva, ahol $\theta \in $[0;$\pi$[ és $\phi \in$ [0;$2\pi$[ . A szög szerinti lépésköz mindkét változóban $\frac{2\pi}{100}$, azaz, a nyégyzetrács [50 $\times$ 100] elemet tartalmaz.

A differenciálegyenletben használt formulák numerikus alakban az FTCS módszer alapján a következő formát öltik:

\begin{equation} \frac{\partial T(t)}{\partial t} = \frac{T_{i,j}(t+\Delta t) - T_{i,j}(t)}{\Delta t} \end{equation}\begin{equation} \frac{\partial T(t)}{\partial \theta} = \frac{T_{i+1,j}(t) - T_{i-1,j}(t)}{\Delta \theta} \end{equation}\begin{equation} \frac{\partial^2 T(t)}{\partial \theta^2} = \frac{T_{i+1,j}(t) - 2T_{i,j}(t) + T_{i-1,j}(t)}{\Delta \theta^2} \end{equation}\begin{equation} \frac{\partial^2 T(t)}{\partial \phi^2} = \frac{T_{i,j+1}(t) - 2T_{i,j}(t) + T_{i,j-1}(t)}{\Delta \phi^2} \end{equation}

Ez alapján a numerikusan megoldani kívánt egyenlet a következő:

$\frac{T_{i,j}(t+\Delta t) - T_{i,j}(t)}{\Delta t} = \alpha \left[ \frac{T_{i+1,j}(t) - 2T_{i,j}(t) + T_{i-1,j}(t)}{\Delta \theta^2} + \frac{1}{sin^2 \theta} \frac{T_{i,j+1}(t) - 2T_{i,j}(t) + T_{i,j-1}(t)}{\Delta \phi^2} + \frac{1}{tan \theta} \frac{T_{i+1,j}(t) - T_{i-1,j}(t)}{\Delta \theta} \right] + bQ - cT^4$

A megoldás során még a peremfeltételekre kellett odafigyelnem. A $\phi$-hez periódikus határfeltélet tarozik mivel $2\pi$-nél visszatérünk 0-hoz. A $\theta$-hoz tartózó peremfeltétel azonban trükkösebb, itt a gömb alján és tetején a következő és előző lépések átkerülnek a gömb másik oldalára, azaz $\theta$ nem változik viszont az adott $\phi$ érték $\phi +180^o$-ra változik. Fontos továbbá megjegyezni, hogy a differenciál egyenletben szereplő $\sin^2\theta$ és $\tan \theta$ értékekkel való osztál $\theta = 0$ esetén zerus osztást eredményezne. Így a differenciál egyenletben ezen tagokat tartalmazó részeit $\theta = 0$ esetén 0-nak veszem.

Paraméterbeállítások

A differenciál egynlet megoldásához nagyon alacson $\Delta t$ paraméter kell választani, különben a instabillá válik. A szimuláció során igyekeztem a valósághoz hasonló paramétereket beállítani, mint pl.: a $\sigma$ Stefan-Boltzmann állandónak vett értéke. Ezen felül a gomb kezdeti hőmérzékletét 273K-re állítottam a körülötte időben változó hőforrás által adott maximális hőmérsékletet pedig 500K-re állítottam. Ez fűti a golyót és tart ellent a folyamatos hőveszteségek, ahogy az az eredményeknél fog látszani.

A beállított paraméterek a következők:

Megnevezés Szimbólum Érték
Felbontás $\phi$ irányban N 100
Lépésköz ideje $\Delta$ t $10^{-6}$
Hővezetési együttható $\alpha$ 2
Hőforrás maximális erőssége b 500
Hőforrás frekvenciája $\omega$ 100
Hőveszteségi együttható $\sigma$ 5.672E-8
Hőforrás iránya $\theta_0$ $\frac{\pi}{3}$
Kezdeti hőmérséklet $T_0$ 100
Négyzetrács magassága $\Delta \theta$ $\frac{\pi}{N/2}$
Négyzetrcs szélessége $\Delta \phi$ $\frac{2\pi}{N} $
Pillanatkép készítésének lépésköze L 5000
Maximálsi lépészám M $10^6$
Kimeneti fileok kezdő neve - 'res_alpha'

Eredmények

A szimuláció futtatása során minden 5000-dik lépéshez tartozó hőmérséklet értékeket kimentettem egy-egy fileba megyeket indexeltem a sorszámuk alapján. A kimentett hőmérsékleti értéket színskálával jelöltem egy gömb felszínén, a különböző időkhoz tartozó képeket pedig egy gif-be rendeztem. Az eredményül kapott vizulizációk és egyéb ábrák elkészítéséhez jupyter notebook-ot használtam, illetve egy python package-ben hoztam létre az ehhez használt függvényeket (simTools.py).

In [1]:
import numpy as np
import matplotlib.pyplot as plt
import simTools as sT

Képek készítése a kimentett fileokból

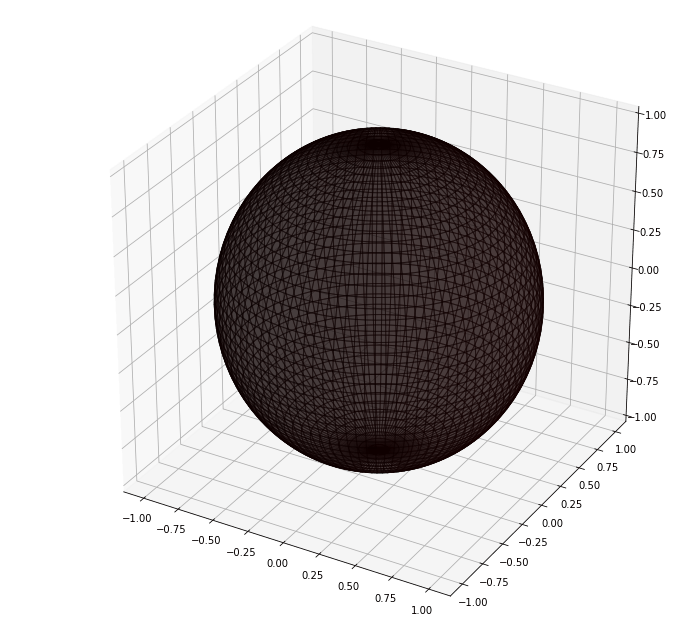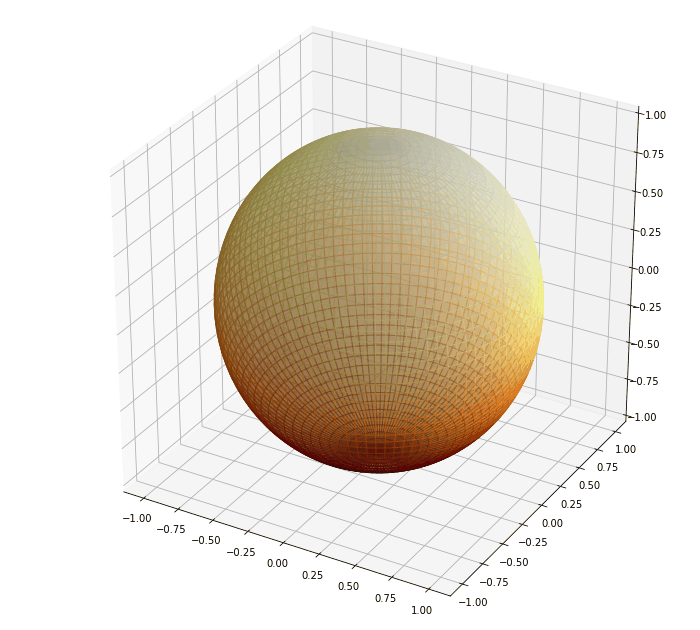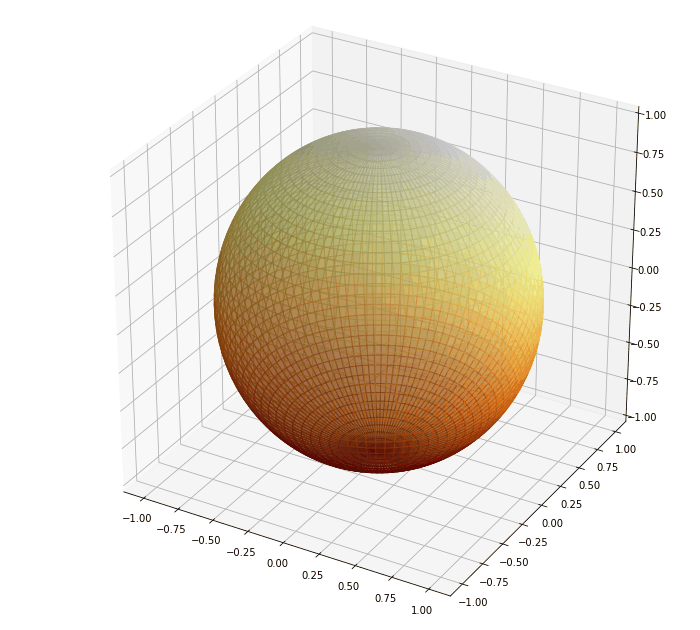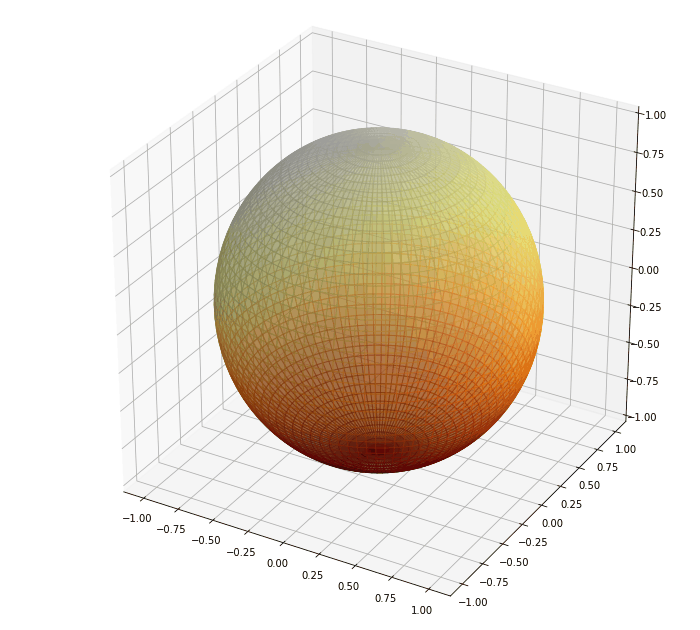
A képeken a szinskála 0-1 között normált a világos színek jeleölik a mgas hőmérsékletet, a sötét az alacsonyt.

In [2]:
# Load temperature data
T = np.loadtxt('snapshots_2/res_alpha_10.dat')

# To creat hetmap normalize T between 0 and 1
maxT = np.max(T)
minT = 265
T = (T - minT) / (maxT - minT)
sT.plotSphereHeat(T, 0) # creat image
A szimláció eredménye egy adott időpontban. Jól látszik a hőforrás $60^o$-os iránya

Időbeli akulás

A képekből GIF-et készítettem.

In [3]:
name = 'alpha' ## file jelző név

# Temperature data loading and saving to images
T = np.loadtxt('snapshots_2/res_'+name+'_'+str(160)+'.dat')
maxT = np.max(T) 
minT = 265
In [5]:
print("Vizualizációs adatok: ")
print('Maximális hőmérséklet', int(maxT))
print('Minumum hőmérséklet', minT)

Vizualizációs adatok: 
Maximális hőmérséklet 455
Minumum hőmérséklet 265
In [ ]:
for i in range(161):
    T = np.loadtxt('snapshots_2/res_'+name+'_'+str(i)+'.dat')
    T = (T - minT) / (maxT - minT) # Normlize T between 0-1
    sT.plotSphereHeat(T, 0, saveTo='images/'+name+"/"+name+'_'+str(10000+i)+'.png') # creat image
In [16]:
sT.create_gif('images/alpha/', 0.2, 'heatBall', 100, 800, 120, 750) # creat a heatBall image
In [19]:
sT.display_gif('heatBall-2018-34-21-20-34-23.gif')
Out[19]:

A hőforrás a megadott frekvenciával körforog a gömb körül közben a hő terjed a cellák között és a kezdeti alacsony hőmérséklethaz képes az egész gömb sokkal melegebb lesz. A maximális hőmérséklet 455 K (fehér), a minimum hőmérséklet 265K (fekete).

Az átlagos hőmérséklet időbeli alakulása

In [3]:
Tlist = []
name = 'alpha'
for i in range(150):
    T = np.loadtxt('snapshots_2/res_'+name+'_'+str(i)+'.dat')
    Tlist.append(np.mean(T))

plt.xlabel('Menetett lépések száma')
plt.ylabel('Átlagos hőmérséklet [K]')
plt.plot(Tlist)
plt.show()

Kezdetben a hőforrás magas hőmérsékletének köszönhetően a gömhély gyorsan felmelekszik, azonban ez hamar beáll egy egynesúlyi értékhez, mivel a hőveszteség a hőmérséklet 4-dik hatványával arányos.

In [ ]: