Általános relativitáselmélet

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
1. Előadás Tematika

Ajánlott irodalom:

• Landau-Lifsic: Elméleti fizika II. Klasszikus erőterek (Tankönyvkiadó, 1976).
• Hraskó Péter: Bevezetés az általános relativitáselméletbe (Műegyetemi kiadó, 1997).
• Hraskó Péter: Relativitáselmélet (Typotex, 2002).
• Perjés Zoltán: Általános relativitáselmélet (ELTE Eötvös Kiadó, 1999).
• http://nedwww.ipac.caltech.edu/level5

Eredeti cikkek:

Általános relativitáselmélet:

A.Einstein, Die Feldgleichungen der Gravitation, Berl. Ber. 44 (1915) 844. ).

Eötvös Loránd szerepe. Az Eötvös-kísérlet, 1908-1909.

[1] R. v. Eötvös, Mathematishe und Naturwissenschaftliche Berichte aus Ungarn, 8,65,1890.

[2] R. v. Eötvös, Verhandlungen der 16. Allgemeinen Konferenz der Internationalen Erdmessung (London-Cambridge, 21-29 September 1909)

[3] R. v. Eötvös, D. Pekár, E. Fekete: Beiträge zum Gesetz der Proportionalität von Trägheit und Gravität; a Beneke Alapítványhoz benyújtott pályamű, 1909.

1.1. Előzmény: a speciális relativitáselmélet (A.Einstein, 1905)

• Események, vonatkoztatási rendszer, inerciarendszer
• Lorentz-transzformáció
$$x'=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}$$ $$y'=y$$ $$z'=z$$ $$t'=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}}$$

A klasszikus elektrodinamika egyenletei kovariánsak a Lorentz-transzformációra nézve (a transzformált mennyiségek közötti kapcsolat ugyanolyan alakú, mint amilyen a nem transzformált mennyiségek között volt).

$\boldsymbol{\rightarrow}$ A fénysebesség minden inerciarendszerben ugyanakkora. Michelson-kísérlet, 1881 és Michelson-Morley-kísérlet, 1887.

• Nincs kitüntetett inerciarendszer: a természet minden törvénye azonos alakú a különböző inerciarendszerekben (relativitás elve) $\boldsymbol{\rightarrow}$ A Lorentz-transzformáció a téridő tulajdonságait jellemzi.

 

Ívhossz: $$s^2=c^2t'^2-{\boldsymbol{r'}}^2=c^2t^2-{\boldsymbol{r}}^2$$







(Levezetések: az ívhossz invarianciája, Lorentz-transzformáció) Másképpen $$ s^2=g_{ik}x^ix^k $$







ahol $$ x^0=ct,\;x^1=x,\;x^2=y,\;x^3=z $$







és $$ g_{ik}={\rm diag}(1,-1,-1,-1) $$







Sajátidő: $$ \tau^2=t^2-\boldsymbol{r}^2/c^2 $$

Minkowski-tér. Időszerű, térszerű, fényszerű ívhosszak.

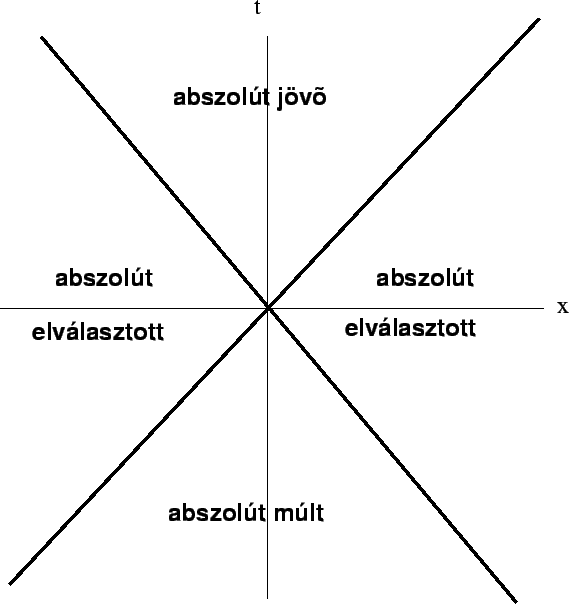Ábra: A téridő egyes tartományainak kauzális kapcsolata az origóban történt eseménnyel.


• Az egyidejűség relativitása

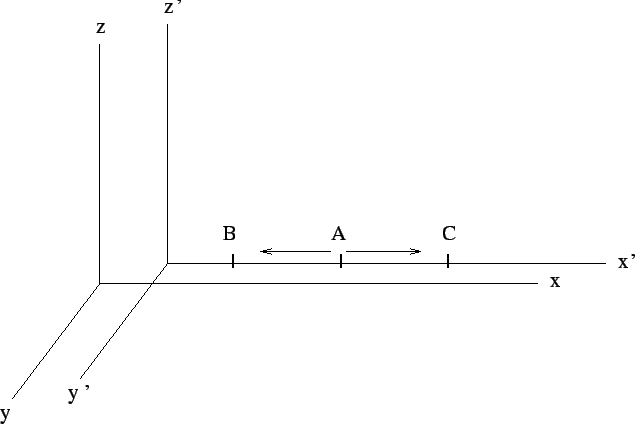Ábra: Az A pontból kibocsájtott fényjelek a K' rendszerből mérve egyidejűleg érnek a B és C pontokba, míg a K rendszerből mérve különböző időpontokban.


$$ x_1\ne x_2,\; t_1=t_2 \boldsymbol{\rightarrow} t_1'\ne t_2' $$

A Lorentz-transzformáció szerint ui. $$ t_2'-t_1'=\frac{-\frac{v}{c^2}(x_2-x_1)}{\sqrt{1-\frac{v^2}{c^2}}} $$

• Lorentz-kontrakció

 

Mozgó méterrúd végei (t,x) a K rendszerből mérve: $(0,0)$ és $(0,L)$

A K' (együttmozgó) rendszerben ugyanezek az események: $(0,0)$ és $(t',L_0)$

A Lorentz-transzformáció alapján $$ L_0=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}} $$

azaz $$ L=L_0\sqrt{1-\frac{v^2}{c^2}} $$

• Idődilatáció

 

Mozgó óra adott (0 ill. $\tau$) mutatóállásai a K rendszerből mérve: $(0,0)$ és $(t,x)$

A K' (együttmozgó) rendszerben ugyanezek az események: $(0,0)$ és $(\tau,0)$

A Lorentz-transzformáció alapján $$ t=\frac{\tau}{\sqrt{1-\frac{v^2}{c^2}}} $$

• Ikerparadoxon
• Sebességek transzformációja

 

$$ v_x=\frac{v'_x+V}{1+\frac{v'_xV}{c^2}} $$
 
 

$$ v_y=\frac{v'_y\sqrt{1-\frac{V^2}{c^2}}}{1+\frac{v'_xV}{c^2}} $$
 
 

$$ v_z=\frac{v'_z\sqrt{1-\frac{V^2}{c^2}}}{1+\frac{v'_xV}{c^2}} $$

(a sebesség irányának megváltozása, fényaberráció)

• Négyesvektorok

 

Az idő és a koordináták transzformációs szabálya szerint transzformálódó mennyiségek. $$t, x, y, z$$

$$E, p_x, p_y, p_z$$

$$\phi, A_x, A_y, A_z$$

• Relativisztikus mechanika

 

Négyessebesség: $$ u^i=\frac{dx^i}{d\tau} $$
$$ u_x=\frac{v}{c\sqrt{1-\frac{v^2}{c^2}}} $$
$$ u_t=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} $$







Négyesimpulzus: $$ p^i=m u^i $$







Az időszerű komponens az energia.

Legkisebb hatás elve. $$ S=-mc\int_a^b ds $$
 
 

$$ L=-mc^2\sqrt{1-\frac{v^2}{c^2}} $$

$c\rightarrow \infty$ határátmenet.

1.2. Gyorsuló koordinátarendszerek

• Az eredeti kérdésfeltevés: megfogalmazhatók-e a természeti törvények olyan alakban, amely tetszőleges koordinátatranszformációra nézve kovariáns?
• Forgó koordinátarendszer

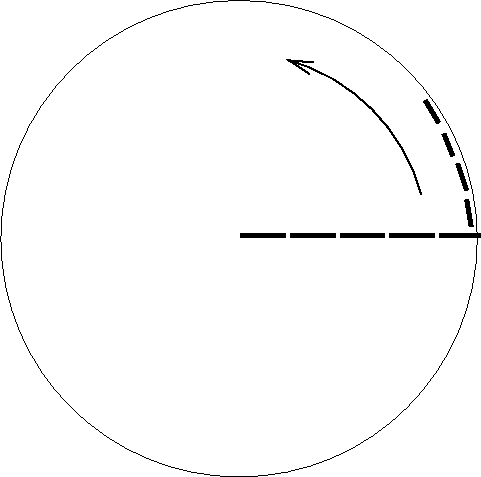Ábra: A forgó korong kerülete mentén elhelyezett mérőrudak Lorentz-kontrakciót szenvednek, míg a sugár mentén elhelyezett mérőrudak hossza változatlan.


$$ x=x'\cos \omega t-y'\sin \omega t, y=x'\sin \omega t+y'\cos \omega t, z=z' $$







Ívelemnégyzet: $$ ds^2=\left[c^2-\omega^2(x'^2+y'^2)\right]dt^2-dx^2-dx'^2-dy'^2-dz'^2+2\omega y'dx' dt-2\omega x'dy' dt $$







Az ívelemnégyzet invariáns (skalár), de a koordinátadifferenciálokkal kifejezett alakja más és más.

• Metrikus tenzor
Általános esetben $$ ds^2=g_{ik}dx^idx^k $$
• Az ekvivalencia elve

 

(Hasonlóságok és különbségek)

• Görbevonalú koordináták

  $$ x^i=f^i(x'^0,x'^1,x'^2,x'^3) $$
 
 

$$ dx^i=\frac{\partial x^i}{\partial x'^k}dx'^k $$

Kontravariáns négyesvektor:
 

$$ A^i=\frac{\partial x^i}{\partial x'^k}A'^k $$

Négyestenzorok. Kontravariáns metrikus tenzor:
 

$$ g^{ik} $$

Jacobi-determináns:

(levezetés) $$ J=\frac{\partial(x^0,x^1,x^2,x^3)}{\partial(x'^0,x'^1,x'^2,x'^3)}=\frac{1}{\sqrt{-g}} $$

Invariáns térfogatelem:
 

$$ \sqrt{-g}d\Omega $$

• Távolságok és időtartamok

 

Adott pontban eltelt idő:

(levezetés) $$ \tau=\frac{1}{c}\int \sqrt{g_{00}}dx^0 $$

Két pont távolsága:

(levezetés) $$ dl^2=\gamma_{\alpha \beta}dx^\alpha dx^\beta $$
  $$ \gamma_{\alpha \beta}=-g_{\alpha \beta}+\frac{g_{0 \alpha}g_{0 \beta}}{g_{0 0}} $$
  $$ \gamma^{\alpha \beta}=-g^{\alpha \beta} $$

• Egyidejűség, órák szinkronizálása

 

(levezetés) $$ \Delta x^0=-\frac{g_{0 \alpha}dx^\alpha}{g_{0 0}} $$