Áramlások fizikája

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
3. Előadás

3.1. Ismétlés

• Ideális folyadék mozgásegyenletei: $$\frac{\partial {\bf v}}{\partial t}+({\bf v} \;grad){\bf v}={\bf f}\; - \frac{1}{\rho}\;grad\; p$$ $$\frac{\partial \rho}{\partial t}+div(\rho {\bf v})=0$$ $$\frac{ds}{dt}=0$$
• Bernoulli-egyenlet:
  (stacionárius áramlás konzervatív tömegerővel) $$\frac{v^2}{2}+V+w= \text{állandó az áramvonal mentén} $$
• Örvénymentes áramlás: $$rot {\bf v}=0\quad\Rightarrow\quad{\bf v}=grad\;\Phi$$ $$\frac{\partial \Phi}{\partial t}+\frac{v^2}{2}+V+w=F(t)$$
• Összenyomhatatlan folyadék örvénymentes áramlása: $$\left.\begin{array}{l} div\; {\bf v}=0\\ rot\; {\bf v}=0 \end{array}\right\}\quad\Rightarrow \quad\triangle \Phi=0\quad +\text{határfeltételek}$$

3.2. Örvénymentes áramlások (folytatás)

• Cirkuláció örvénymentes áramlásban:
  Adott C görbére: $$\Gamma_C=\oint_C {\bf v}\cdot d{\bf s}$$
Ha a C zárt görbére fektethető olyan felület, amely teljesen az áramlás tartományában van, akkor $$\Gamma_C=\oint_C {\bf v}\cdot d {\bf s}=\int rot {\bf v} \cdot d {\bf F}=0$$ Felhasználtuk Stokes tételét.
Az ilyen tulajdonságú görbék a folyadék belsejében folytonos deformációval egy ponttá húzhatók össze. Ha ez minden zárt görbére teljesül, akkor azt mondjuk, hogy a tartomány (jelen esetben az áramlási tér) egyszeresen összefüggő.

3.3. Síkbeli áramlások

• Síkbeli áramlás: az áramlás jellemzői a $z$ tengelyre merőleges síkban azonosak, semmi nem függ $z$-től. $\Phi=\Phi(x,y)$ $$\frac{\partial^2 \Phi}{\partial x^2}+\frac{\partial^2 \Phi}{\partial y^2}=0$$ Komplex potenciál és sebesség: $$z=x+iy$$ Itt $z$ nem a $z$ koordináta, hanem egy komplex szám! $$f(z)=\Phi(x,y)+i\Psi(x,y)$$ $$\frac{df}{dx}=\frac{\partial \Phi}{\partial x}+i\frac{\partial \Psi}{\partial x}=\frac{df}{dz}\quad y=konst.$$ $$\frac{df}{idy}=-i\frac{\partial \Phi}{\partial y}+\frac{\partial \Psi}{\partial y}=\frac{df}{dz}\quad x=konst.$$ $$\frac{\partial \Phi}{\partial x}=\frac{\partial \Psi}{\partial y}\quad \text{és}\quad\frac{\partial \Phi}{\partial y}=-\frac{\partial \Psi}{\partial x} $$ Cauchy-Riemann-feltételek.
  Következmény: $$\frac{\partial^2 \Phi}{\partial x^2}=\frac{\partial^2 \Psi}{\partial x\partial y}\quad ,\quad\frac{\partial^2 \Phi}{\partial y^2}=-\frac{\partial^2 \Psi}{\partial y\partial x} \Rightarrow \frac{\partial^2 \Phi}{\partial x^2}+\frac{\partial^2 \Phi}{\partial y^2}=0\quad ,\quad \frac{\partial^2 \Psi}{\partial x^2}+\frac{\partial^2 \Psi}{\partial y^2}=0$$ Továbbá $$grad \Phi \cdot grad \psi=\frac{\partial \Phi}{\partial x}\frac{\partial \Psi}{\partial x}+\frac{\partial \Phi}{\partial y}\frac{\partial \Psi}{\partial y}=0\;,$$ tehát a $\Phi=const.$ és $\Psi=const.$ vonalak egymásra merőlegesek. $\Phi= \mathrm{Re} f$ egy lehetséges áramlás sebességpotenciálja, $\Psi= \mathrm{Im} f$ az ún. áramlási függvény. Szintvonalai merőlegesek $\Phi$ szintvonalaira, azaz áramvonalak. Tehát $$\Psi=konst.$$ az áramvonalak egyenlete.
  $w=f(z)$ az áramlás komplex potenciálja.
  Komplex sebesség: $$\frac{dw}{dz}=\frac{df}{dz}=\frac{\partial \Phi}{\partial x}+i\frac{\partial \Psi}{\partial x}=\underbrace{\frac{\partial \Phi}{\partial x}}_{v_x}-i\underbrace{\frac{\partial \Phi}{\partial y}}_{v_y}=v_x-iv_y$$
• Példák:
  • 
    $ \begin{eqnarray} w=C\;z\qquad \qquad \Phi&=&{\rm Re}\; C\; x-{\rm Im}\; C\; y\\ \Psi&=&{\rm Im}\; C\; x+{\rm Re}\; C\; y\\ \frac{dw}{dz}=\;C\;={\rm Re}\; C\;&+&\;i\;{\rm Im}\; C\; \end{eqnarray} $
    Párhuzamos áramlás
    
    
  • 
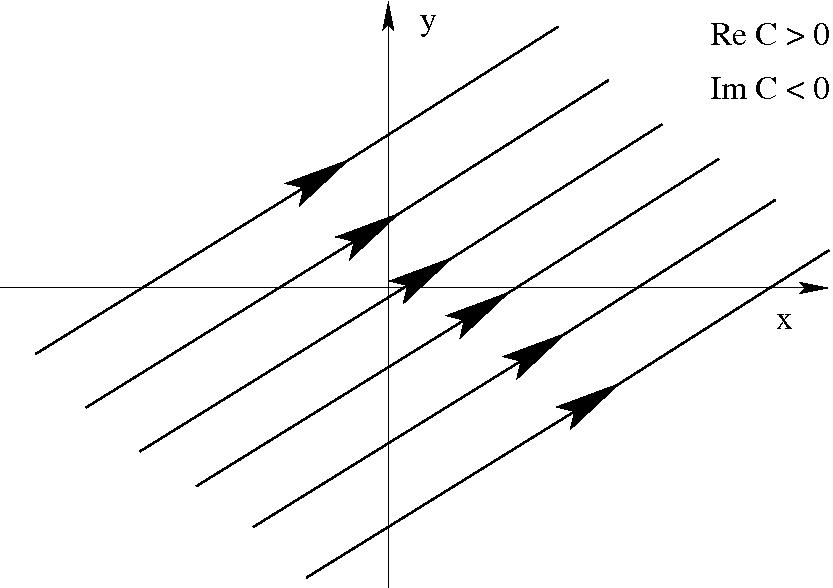
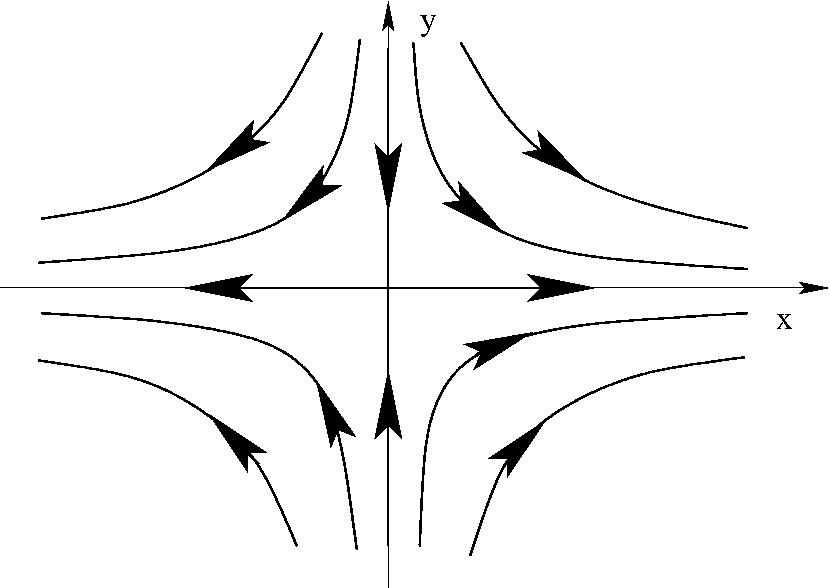
    $ \begin{eqnarray} w=C\;z^2\quad (C\;{\rm valós}) \quad \Phi&=&\; C\; (x^2-y^2)\\ \Psi&=&\;2 C\; x\; y\\ \frac{dw}{dz}=\;2C\;z=2C\;(x&+&iy) \end{eqnarray} $
    Torlódás síknál
    Áramlás 90$^\circ$-os sarokban
    
    
  • 
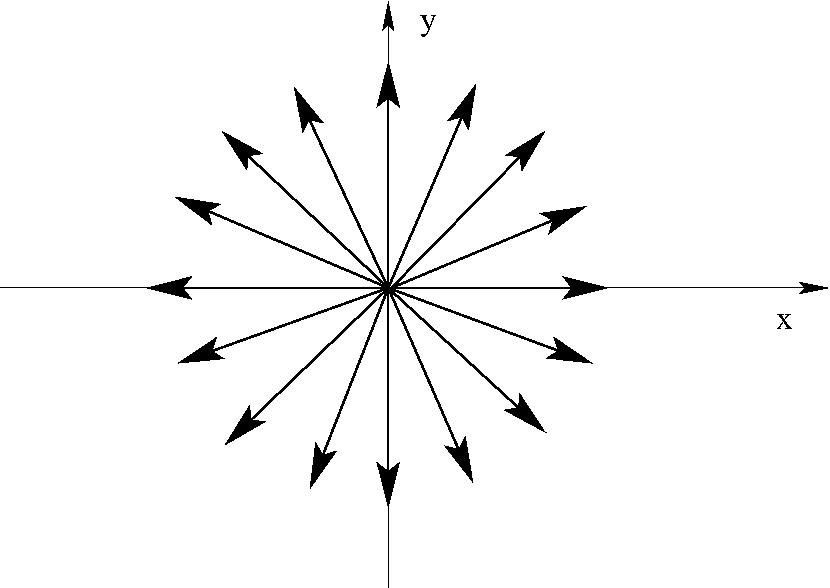
    $ \begin{eqnarray} w=C\;\ln\;z\quad (C\;{\rm valós,\; pozitív}) \quad \Phi&=&\; C\; \ln\;r\\ \Psi&=&\; C\; \varphi\\ \frac{dw}{dz}=\;\frac{C}{z}=\frac{C}{|z|^2}(x&-&iy) \end{eqnarray} $
    Síkbeli forrás
    
    
  • 
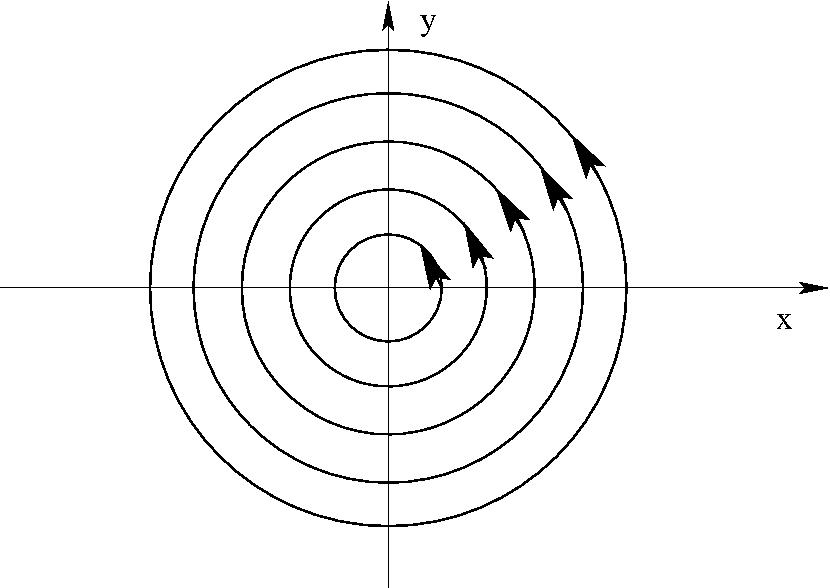
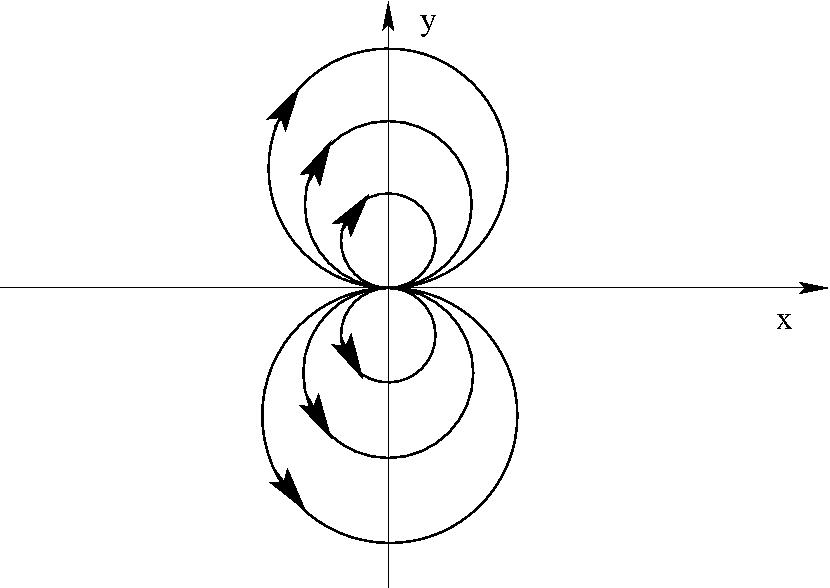
    $ \begin{eqnarray} w=-iC\;\ln\;z\quad (C\;{\rm valós,\; pozitív}) \quad \Phi&=&\; C\; \varphi\\ \Psi&=&\; -C\;\ln\;r\\ \frac{dw}{dz}=\;\frac{-iC}{z}=\frac{C}{|z|^2}(-y&-&ix) \end{eqnarray} $
    Síkbeli cirkulációs áramlás
    
    
  • 
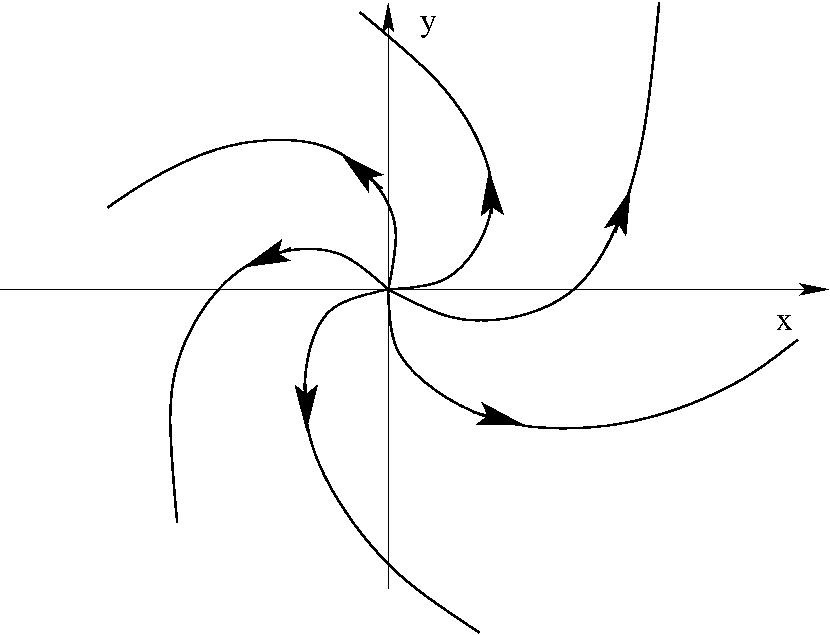
    $ \begin{eqnarray} w=\frac{C}{z}\quad (C\;{\rm valós}) \quad \Phi&=&\; \frac{C}{r}\; \cos\;\varphi\\ \Psi&=&\; -\frac{C}{r}\; \sin\;\varphi\\ \frac{dw}{dz}=\;-\frac{C}{z^2}=\frac{C}{|z|^2}((y^2-x^2)&+&2ixy) \end{eqnarray} $
    Dipólus: közeli forrás és nyelő
    
    
  • $$w=(C_1+iC_2)\ln\;z$$
    
    
• Henger áramló folyadékban
  
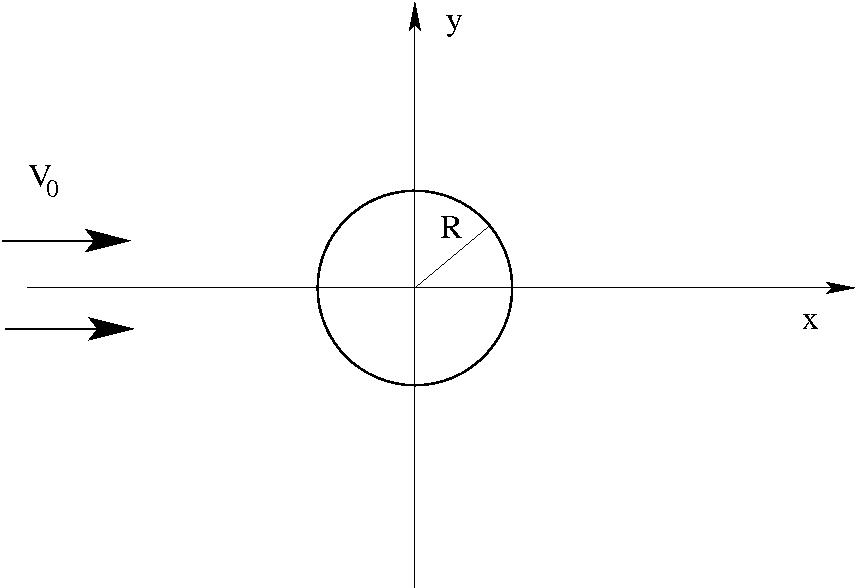
  A hengertől nagy távolságban a sebesség $x$ irányú, homogén. Ezért a komplex sebességben nem szerepelhet $z$ pozitív hatványa (akkor $v_\infty=\infty$ lenne). Így csak konstans és negatív hatványok lehetnek: $ \begin{eqnarray} \frac{dw}{dz}&=&v_0+\frac{C_{-1}}{z}+\frac{C_{-2}}{z^2}+\ldots\\ w&=&v_0\;z+C_{-1}\ln z-\frac{C_{-2}}{z}-\frac{C_{-3}}{2z^2}-\ldots\\ z&=&r{\rm e}^{i\varphi}\\ C_{-k}&=&A_k+iB_k \end{eqnarray} $
  Az áramlási függvény: $$\Psi={\rm Im}\; w=v_0\;r\sin\varphi +A_1\varphi+B_1\ln r+\frac{A_2}{r}\sin\varphi-\frac{B_2}{r}\cos\varphi+\frac{A_3}{2r^2}\sin2\varphi$$
  Peremfeltétel: $r=R$-re $v_n=0$, azaz a sebesség érintőirányú, tehát $\left.\Psi\right|_R=konst.$ az $R$ sugarú körön. Ebből következik: $$A_1=0\;,\quad v_0R+\frac{A_2}{R}=0\;,\quad B_2=0\;,\quad A_3=A_4=\ldots=0\;,\quad B_3=B_4=\ldots=0\;$$ $$A_2=-v_0R^2\;.\quad {\rm Írjuk,\; hogy}\quad B_1=-\frac{\Gamma}{2\pi}$$
  A peremfeltételt kielégítő alak tehát $$w=v_0z+\frac{v_0R^2}{z}-i\frac{\Gamma}{2\pi}\ln z$$