Áramlások fizikája

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
4. Előadás

4.1. Ismétlés

• Cirkuláció: $$\Gamma_C=\oint_C {\bf v}\cdot d{\bf s}$$
• Tetszőleges $w(z)$ differenciálható komplex függvény valamilyen síkbeli potenciáláramlást ír le a következő szabályok szerint:
  • $$z=x+iy$$
  • $$w(z)=\Phi(x,y)+i\Psi(x,y)$$ A $w(z)$ komplex függvény valós része a $\Phi(x,y)$ sebességpotenciál, képzetes része a $\Psi(x,y)$ áramlási függvény.
  • $$\Psi(x,y)=konst.$$ az áramvonalak egyenlete
  • $$\frac{dw}{dz}=v_x-iv_y$$ határozza meg a sebességkomponenseket.
  • Az áramló folyadékot határoló szilárd falakon a sebesség normális komponense eltűnik, tehát a falakon a sebesség érintő irányú, ami azt jelenti, hogy a falak mentén halad egy áramvonal, így ott a $\Psi(x,y)$ áramlási függvény konstans.
• Példák síkbeli potenciáláramlásra:
  • Párhuzamos (homogén) áramlás: $$w=C\;z$$
  • Torlódás síknál ill. áramlás 90$^\circ$-os sarokban: $$w=C\;z^2\quad (C\;{\rm valós})$$
  • Síkbeli forrás/nyelő: $$w=C\;\ln\;z\quad (C\;{\rm valós})$$
  • Síkbeli cirkulációs áramlás: $$w=-iC\;\ln\;z\quad (C\;{\rm valós})$$
  • Dipólus: $$w=\frac{C}{z}\quad (C\;{\rm valós})$$
  • Henger körüli áramlás: $$w=v_0z+\frac{v_0R^2}{z}-i\frac{\Gamma}{2\pi}\ln z$$

4.2. Síkbeli áramlások (folytatás)

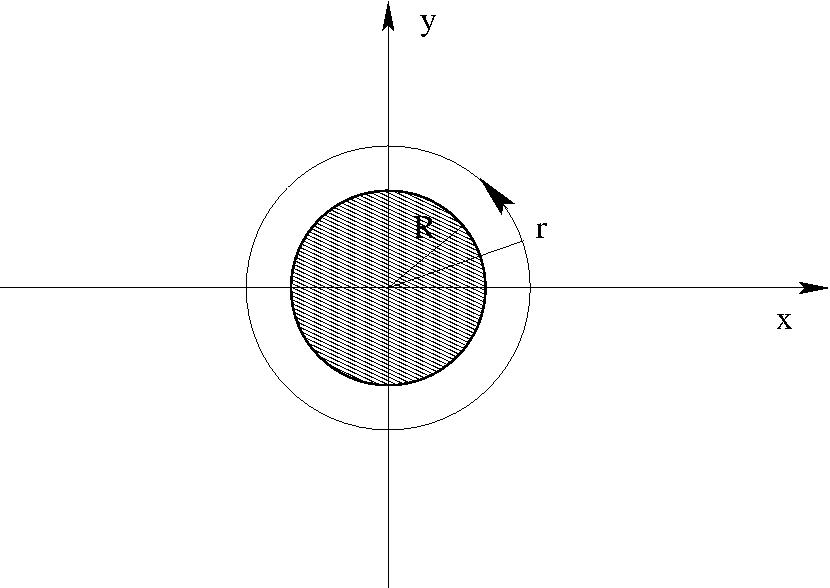
• Henger áramló folyadékban
  A sebességpotenciál: $$\Phi={\rm Re}\; w=v_0\cos\varphi\left(r+\frac{R^2}{r}\right)+\frac{\Gamma}{2\pi}\varphi$$
  Az áramlási függvény: $$\Psi={\rm Im}\; w=v_0\sin\varphi\left(r-\frac{R^2}{r}\right)-\frac{\Gamma}{2\pi}\ln r$$
  Sebességkomponensek:
  $ \begin{eqnarray} v_r&=&\frac{\partial \Phi}{\partial r}=v_0\cos\varphi\left(1-\frac{R^2}{r^2}\right)\\ v_\varphi&=&\frac{1}{r}\frac{\partial \Phi}{\partial \varphi}=-v_0\sin\varphi\left(1+\frac{R^2}{r^2}\right)+\frac{\Gamma}{2\pi\;r} \end{eqnarray} $
  A cirkuláció nem redukálható zárt görbén:
  
  $$\oint {\bf v} d{\bf s}=\int_0^{2\pi}v_\varphi r d\varphi =\Gamma-v_0\left(1+\frac{R^2}{r^2}\right)r\int_0^{2\pi}\sin\varphi \;d\varphi=\Gamma$$
  Torlópontok: zérus sebességű pontok. $$\frac{dw}{dz}=v_0-\frac{v_0R^2}{z^2}-i\frac{\Gamma}{2\pi}\frac{1}{z}=0\quad\Rightarrow\quad z^2-i\frac{\Gamma}{2\pi}z-R^2=0$$ $$z_\pm=i\frac{\Gamma}{4\pi v_0}\pm \sqrt{R^2-\left(\frac{\Gamma}{4\pi v_0}\right)^2}$$
  Ha $\Gamma=0$:
  
  
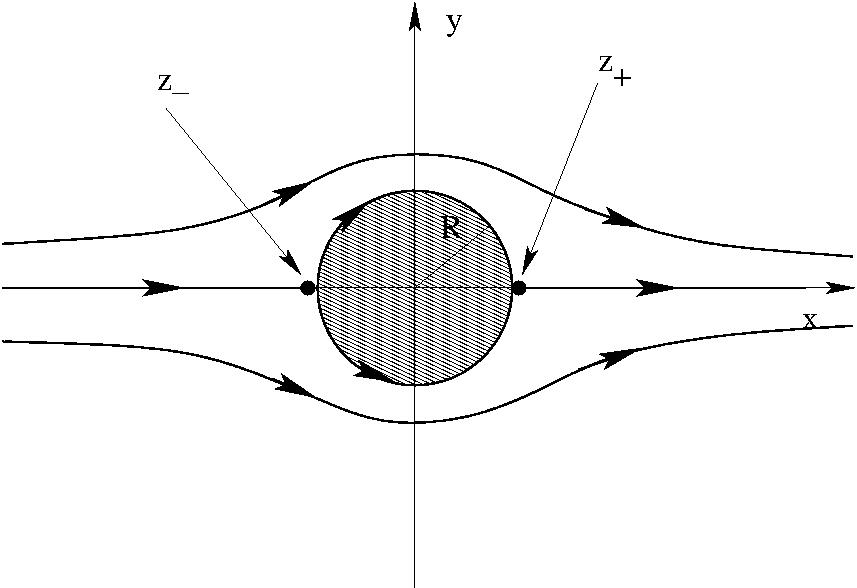
  Ha $0 < \Gamma < 4\pi v_0 R$:
  
  
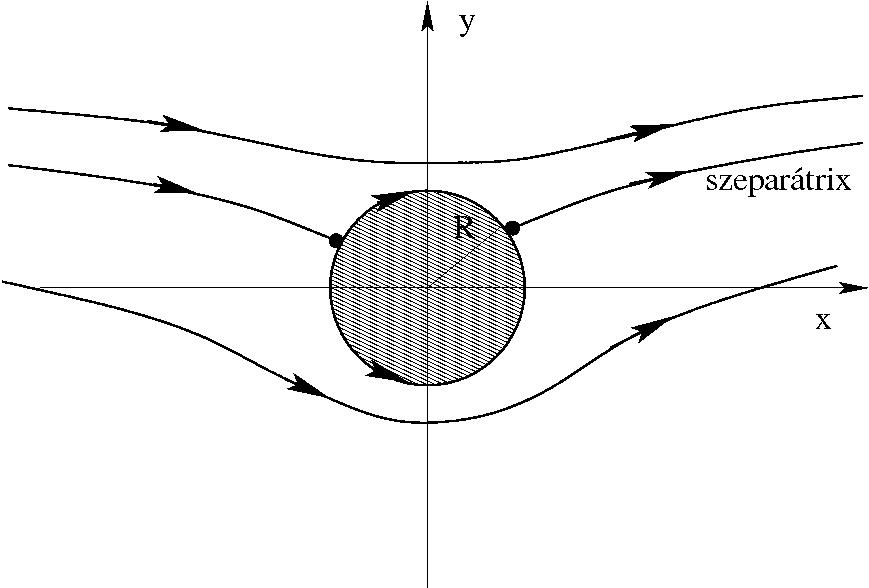
  Ha $\Gamma = 4\pi v_0 R$:
  
  
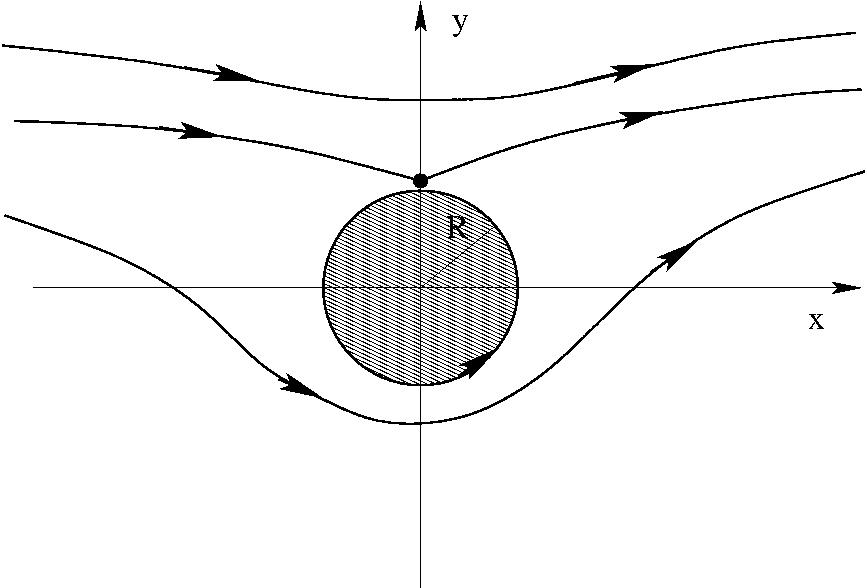
  Ha $\Gamma > 4\pi v_0 R$:
  
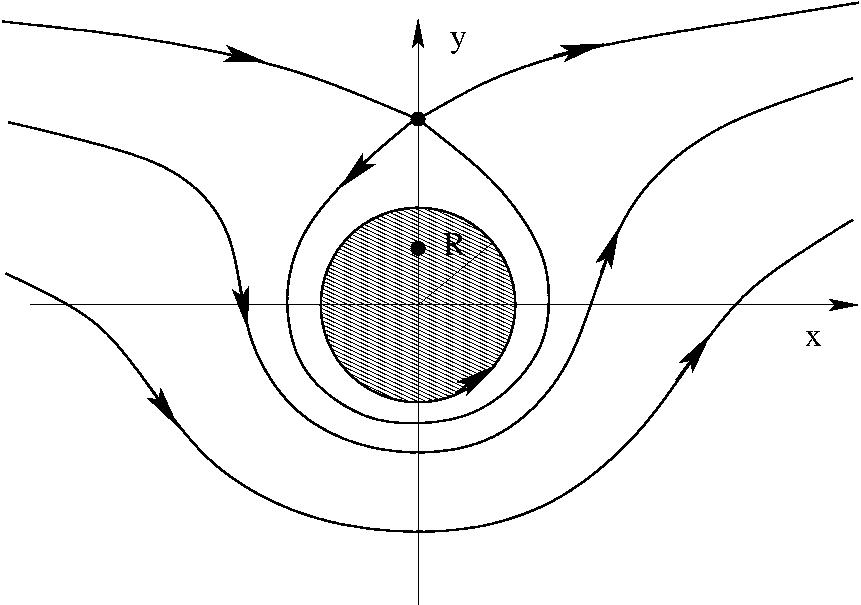
  A henger egységnyi hosszára ható erő kiszámítása:
  A Bernoulli-egyenletből:
  $ \begin{eqnarray} \frac{1}{2}\rho v^2+p&=&\frac{1}{2}\rho v_0^2+p_0=konst. \quad {\rm mindenütt}\\ p&=&C-\frac{1}{2}\rho v^2 \end{eqnarray} $
  A henger felületén $v^2=\left(\frac{\Gamma}{2\pi R}-2v_0\sin\varphi\right)^2$ $${\bf F}=-\oint p{\bf n} ds\;,\quad ds=R\;d\varphi$$
  $ \begin{eqnarray} F_x&=&\frac{1}{2}\rho R\int_0^{2\pi}\left(\frac{\Gamma}{2\pi R}-2v_0\sin\varphi\right)^2\cos\varphi\; d\varphi-\int_0^{2\pi}C\cos\varphi\;R d\varphi=0\\ F_y&=&\frac{1}{2}\rho R\int_0^{2\pi}\left(\frac{\Gamma}{2\pi R}-2v_0\sin\varphi\right)^2\sin\varphi\; d\varphi-\int_0^{2\pi}C\sin\varphi\;R d\varphi=-\rho v_0 \Gamma \end{eqnarray} $
  Csak az áramlásra merőleges (felhajtó-) erő hat. A cirkulációt adottnak véve jó egyezés a tapasztalattal. A cirkulációt a súrlódás hozza létre, amit itt elhanyagoltunk.
• Konform leképezések
  Holomorf függvények által létrehozott leképezés: lokálisan nagyító, de szögtartó és az irányítottságot is tartja (ha $f'(z)\ne 0$).
  A komplex potenciál mint leképezés: $w=w(z)$
  
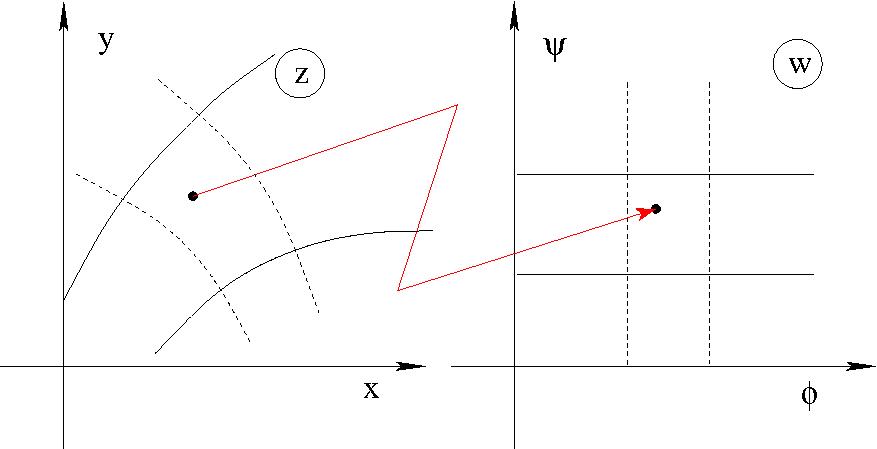
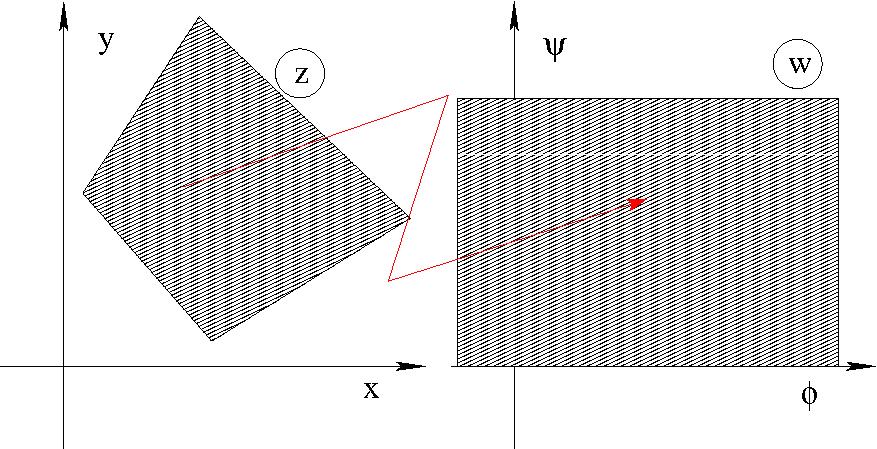
  Ahol az áramlást szilárd, mozdulatlan falak határolják, ott a sebesség tangenciális, tehát a fal valamelyik áramvonallal azonos, ezért ott $\Psi=const.$ Egyszeresen összefüggő tartomány esetén egyetlen áramvonal fut a falak mentén, a konstans pedig nullának választható. Ez azt jelenti, hogy a komplex potenciál az áramlás $(x,y)$ síkban fekvő tartományát a $w$ sík felső félsíkjába képezi: