Áramlások fizikája

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
5. Előadás

5.1. Ismétlés

• Hengerre ható erők: $ \begin{eqnarray} F_x&=&0\\ F_y&=&-\rho v_0 \Gamma \end{eqnarray} $
• Konform leképezések:
  • Holomorf komplex függvények, a leképezés szög- és irányítottságtartó.
  • Ha a $w(z)$ leképezés adott tartományt a felső komplex félsíkba képez, akkor $w(z)$ az adott tartományban végbemenő stacionárius örvénymentes áramlás komplex potenciálja.

5.2. Konform leképezések (folytatás)

• 
  Példák
  • Cirkulációs áramlás: $$w=w(z)=\frac{\Gamma}{2\pi i}\ln z=\frac{\Gamma \varphi}{2\pi}-i\frac{\Gamma}{2\pi}\ln r$$
  • Áramlás sarokban ill. élnél: $$w(z)=A z^{\frac{\pi}{\alpha}}=Ar^{\frac{\pi}{\alpha}}{\rm e}^{i\frac{\pi}{\alpha}\varphi}$$ $$\Phi=Ar^{\frac{\pi}{\alpha}}\cos{\frac{\pi}{\alpha}\varphi}\;,\quad \Psi=Ar^{\frac{\pi}{\alpha}}\sin{\frac{\pi}{\alpha}\varphi}$$ $$v_r=\frac{\partial \Phi}{\partial r}=\frac{\pi}{\alpha}Ar^{\frac{\pi}{\alpha}-1}\cos{\frac{\pi}{\alpha}\varphi}\;,\quad v_\varphi=\frac{1}{r}\frac{\partial \Phi}{\partial \varphi}=-\frac{\pi}{\alpha}Ar^{\frac{\pi}{\alpha}-1}\sin{\frac{\pi}{\alpha}\varphi}$$
    $\quad$sarok: $\quad\frac{\pi}{\alpha}>1\;\Rightarrow \;v(0)=0\;,\;v(\infty)=\infty$
    $\quad$él: $\quad\frac{\pi}{\alpha}<1\;\Rightarrow \;v(0)=\infty\;,\;v(\infty)=0$
    
  • Áramlás szárnyprofil körül
    Kutta-Zsukovszkij-transzformáció: $$z=w+\frac{1}{w}$$
    
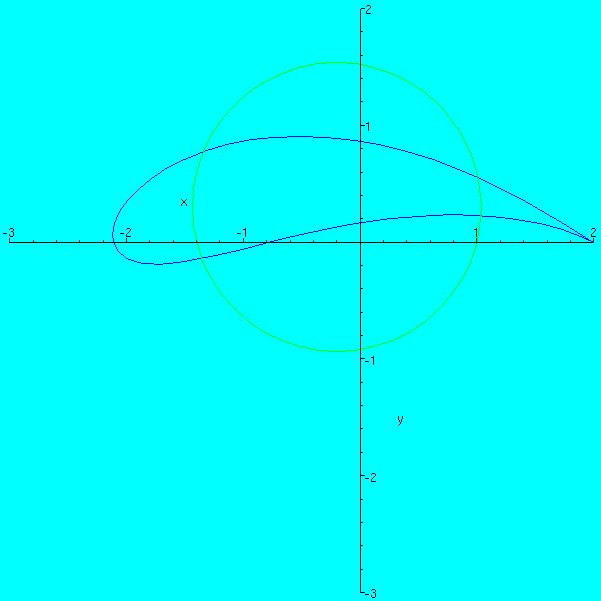
    A kört szárnyprofilba transzformálja.
    Az inverz transzformált $$w=-w_0+\frac{1}{2}\left(z+\sqrt{z^2-4}\right)$$ a szárnyprofilt az origó középpontú körbe transzformálja. A kör (henger) körüli áramlás komplex potenciálja ismert, így a szárnyprofil körüli örvénymentes áramlás komplex potenciálja: $$v_0\left(w+\frac{R^2}{w}\right)-i\frac{\Gamma}{2\pi}\ln w = v_0\left(-w_0+\frac{1}{2}\left(z+\sqrt{z^2-4}\right)+\frac{R^2}{-w_0+\frac{1}{2}\left(z+\sqrt{z^2-4}\right)}\right)-i\frac{\Gamma}{2\pi}\ln \left(-w_0+\frac{1}{2}\left(z+\sqrt{z^2-4}\right)\right) $$ $\Gamma=0$:
    
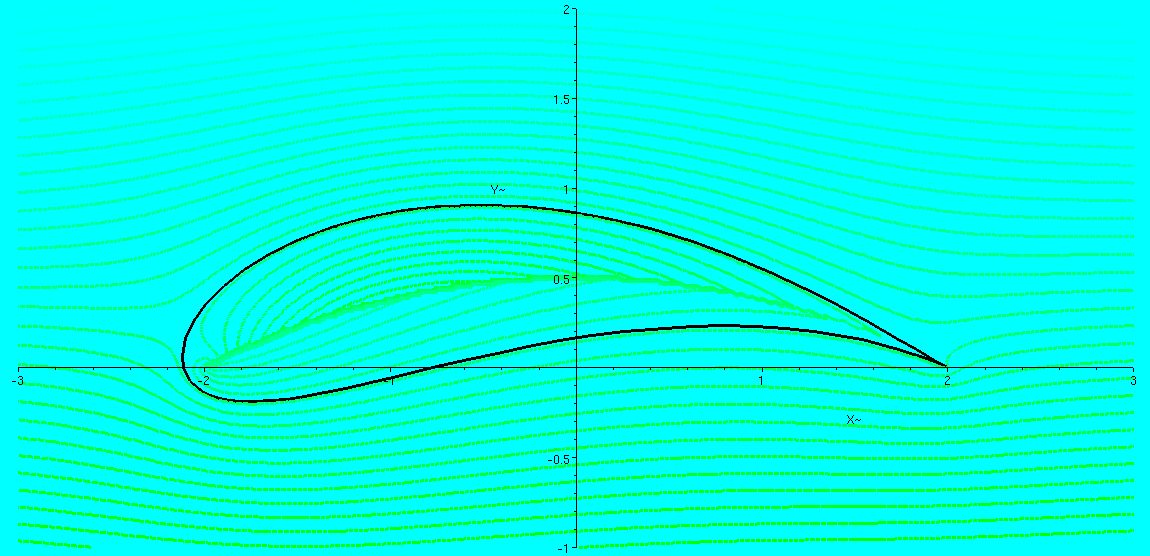
    $\Gamma<0$:
    
    

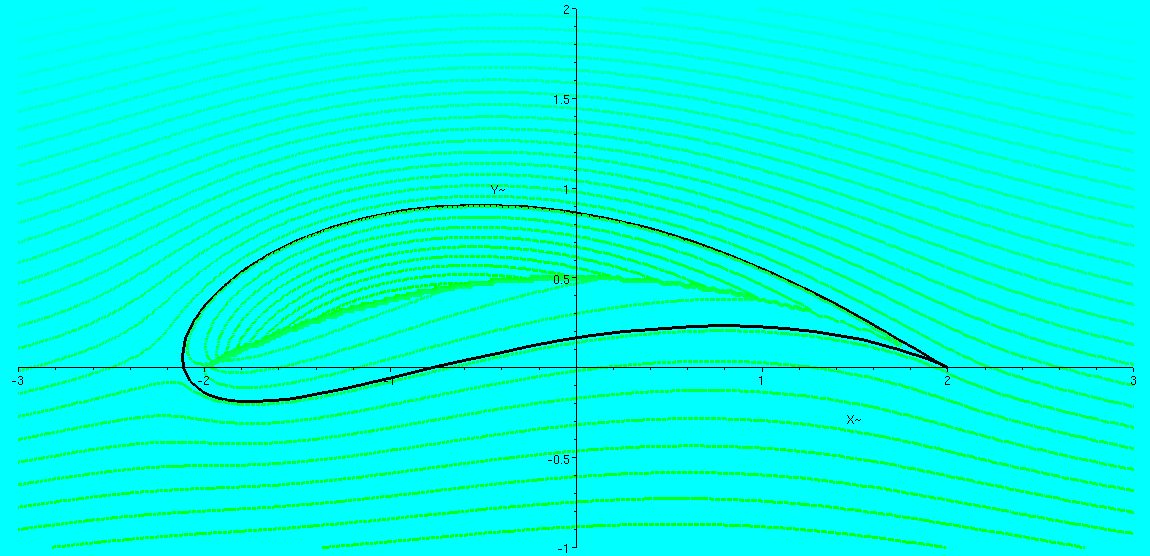
5.3. Zsukovszkij-tétel

• Tetszőleges keresztmetszetű henger áramló folyadékban
  $C$ görbével határolt keresztmetszet esetén $w(z)=?$
  potenciál körkeresztmetszet esetén: $F(\zeta)=v_0\left(\zeta+\frac{R^2}{\zeta}\right)-i\frac{\Gamma}{2\pi}\ln \zeta$
  Találjunk olyan konform leképezést, mely a $C$ görbét az $R$ sugarú körbe viszi és $z\rightarrow \infty$-re $z=\zeta$ (így lesz mindkét esetben $v_0$ a beáramlási sebesség). Legyen ez $\zeta=h(z)$. Az új probléma potenciálja ekkor előáll, mint $$w(z)=F(h(z))$$ Így a $z$ síkot $\zeta$ közbeiktatásával leképeztük a párhuzamos áramlásra.
  $w(z)$ ismeretében a felhajtóerő számolható (Kutta-Zsukovszkij-erő) és $$F_y=-\rho v_0 \Gamma$$

5.4. Thomson-tétel: a cirkuláció megmaradása

• Cirkuláció időbeli viselkedése
  A cirkulációt adott $t$ pillanatra kiszámítjuk valamilyen zárt $C_t$ görbe mentén, majd a görbét alkotó folyadékrészek mozgását követjük, és kiszámítjuk a cirkulációt az így létrejött $C_{t+dt}$ görbe mentén is: $$\Gamma_t=\oint_{C_t}{\bf v}d{\bf s}$$ $$\Gamma_{t+dt}=\oint_{C_{t+dt}}{\bf v'}d{\bf s'}$$ A ${\bf v'}$ és $d{\bf s'}$ mennyiségeket a $t$ időpontbeli értékekkel fejezzük ki: $${\bf v'}={\bf v}+\frac{d{\bf v}}{dt}dt\;,\quad d{\bf s'}=d{\bf s}+\underbrace{({\bf v}_B-{\bf v}_A)}_{d{\bf v}}dt$$ $$\Downarrow$$ $${\bf v'}d{\bf s'}={\bf v}d{\bf s}+\frac{d{\bf v}}{dt}d{\bf s}dt+{\bf v}d{\bf v}dt+\mathcal{O}(dt^2)$$
  Integrálva: $$ \Gamma_{t+dt}=\Gamma_{t}+\left(\oint_{C_t}\frac{d{\bf v}}{dt}d{\bf s}+\oint_{C_t}{\bf v}d{\bf v}\right)dt $$ A zárójelen belüli második tag eltűnik, mert teljes differenciál integrálja zárt görbe mentén: $$\oint_{C_t}{\bf v}d{\bf v}=\frac{1}{2}\oint_{C_t}d{ v^2}=0$$ $$\Downarrow$$ $\begin{eqnarray} \frac{d \Gamma_{t}}{dt}=\oint_{C_t}\frac{d{\bf v}}{dt}d{\bf s}&=&\oint_{C_t}{\bf f}\;d{\bf s}-\oint_{C_t}\frac{1}{\rho}{\rm grad}\;p\;d{\bf s}\\ &\uparrow&\\ \text{Euler}&\text{-}&\text{egyenlet} \end{eqnarray}$
  Megmaradás: ha a tömegerő konzervatív (${\bf f}=-{\rm grad}\; V$) és a folyadék barotróp ($\frac{1}{\rho}{\rm grad}\;p={\rm grad}\;P$), akkor $$\frac{d\Gamma_{t}}{dt}=0\;,$$ azaz a folyadékkal együtt sodródó görbére vonatkozó cirkuláció időben állandó. Ez a Thomson-tétel. Igaz mind örvényes, mind örvénymentes ideális folyadékra.

5.5. Örvényes áramlások

• Az áramlás örvényes, ha van olyan hely az áramlásban, ahol ${\rm rot}{\bf v}\ne 0$.
• Örvényvektor: $${\bf \Omega}=\frac{1}{2}{\rm rot}{\bf v}$$ az adott helyen és időben a folyadék szögsebessége.
• Szemléltetése:
  Örvényvonal: érintője a helyi ${\bf \Omega}$ vektor.
  Örvénycső: palástján ${\bf \Omega}$ érintőirányú.
• Örvényfluxus: $\begin{eqnarray} K=\int {\bf \Omega}d{\bf F}&=&\frac{1}{2}\oint_C {\bf v}d{\bf s}=\frac{1}{2}\Gamma_C\\ &\uparrow&\\ \text{Stokes}&\text{-}&\text{tétel} \end{eqnarray}$