Áramlások fizikája

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
6. Előadás

6.1. Ismétlés

• Példák a konform leképezések alkalmazására: áramlás sarok/él körül, áramlás szárnyprofil körül.
• Zsukovszkij tétele: bármilyen keresztmetszetű hengerre ható felhajtóerő $$F_y=-\rho v_0 \Gamma$$
• Thomson tétele: az áramlással együtt sodródó görbére vett cirkuláció ideális, barotróp folyadékban, konzervatív tömegerő esetén időben állandó.
• Örvényes áramlás alapfogalmai: örvényvektor, örvényvonal, örvénycső, örvényfluxus

6.2. Örvénytételek

• Az örvénycsőbe zárt örvényfluxus adott időpontban a cső mentén állandó (általánosan érvényes, nem ideális folyadékra is): $${\rm div}{\bf \Omega}=0$$ $$\Downarrow$$ $$\int {\rm div}{\bf \Omega}\;dV=\underbrace{\int_{\text{palást}}{\bf \Omega}d{\bf F}}_{=0}+\int_{\text{2}}{\bf \Omega}d{\bf F}-\int_{\text{1}}{\bf \Omega}d{\bf F}=0$$ $$\Downarrow$$ $$K=\int {\bf \Omega}d{\bf F}=\text{állandó a cső mentén}$$ Az örvénycső lehet zárt. Ha nem zárt, akkor csak a folyadék határán végződhet.
• A cirkuláció megmaradásából származó örvénytételek (ideális és barotróp folyadék + konzervatív térfogati erő esetén)
  • Az örvénycsőbe zárt örvényfluxus időben sem változik.
    Örvényfonál: olyan vékony cső, hogy benne $\bf \Omega$ állandó. Az örvényfonalat bárhol és bármely időpontban a $\kappa={\bf \Omega} d{\bf F}$ örvényesség (örvényfluxus) jellemzi. Ideális folyadékban minden örvényfonal örvényessége megadandó mint külső paraméter.
  • Ideális folyadékban örvények nem keletkeznek és nem szűnnek meg.
    Ha $t_0$ időpontban egy folyadéktartományban nincsenek örvények, akkor ott $ \boldsymbol \Omega=0$. Mivel $\Gamma$ ekkor tetszőleges görbére eltűnik, a megmaradás miatt később is eltűnik, ezért később is fenn kell állnia, hogy $ \boldsymbol \Omega=0$.
  • Örvénycsövet alkotó folyadékrészek később is örvénycsövet alkotnak.
    Bizonyítás: vegyünk fel tetszőleges zárt redukálható görbét az örvénycső palástján. Az erre vett cirkuláció nulla. Későbbi időpontban a folyadékkal együttmozgó görbére a cirkuláció Thomson tétele szerint továbbra is nulla lesz. Mivel ez bármely és tetszőlegesen kicsi görbére is igaz, az örvényvektornak a korábbi örvénycső sodródásával létrejött cső palástján a palásttal párhuzamosnak kell lennie, azaz ez a cső is örvénycső.
    Pl.: pipafüst-karika
    Füstkarikák 1.
    Füstkarikák 2.

6.3. Örvények keletkezése ideális folyadékban

A cirkuláció nem marad meg, ha
• a folyadék nem barotróp (azaz baroklin: kezdetben nincs egyensúly)
• a tömegerő nem konzervatív
• baroklin folyadék (de konzervatív tömegerő) $$\frac{d\Gamma}{dt}=-\oint \frac{1}{\rho}{\rm grad} \;p\;d{\bf s} $$ Ezúttal nem igaz, hogy $\rho=\rho(p)$, amiből következne, hogy a $p=\text{állandó}$ (izobár) és a $\rho=\text{állandó}$ (izosztér) felületek egybeesnek. Most tehát ezek a felületek metszik egymást.
  Pl. $$\frac{d\Gamma_{ABCD}}{dt}= -\underbrace{\int_A^B \frac{1}{\rho}{\rm grad} \;p\;d{\bf s}}_{=0} -\underbrace{\int_B^C \frac{1}{\rho}{\rm grad} \;p\;d{\bf s}}_{\frac{p_2-p_1}{\rho_2}} -\underbrace{\int_C^D \frac{1}{\rho}{\rm grad} \;p\;d{\bf s}}_{=0} -\underbrace{\int_D^A \frac{1}{\rho}{\rm grad} \;p\;d{\bf s}}_{\frac{p_2-p_1}{\rho_1}} =\left(\frac{1}{\rho_1}-\frac{1}{\rho_2}\right)(p_2-p_1)\ne 0$$ Általában $\begin{eqnarray} \frac{d\Gamma_{C}}{dt}=-\oint\frac{1}{\rho}{\rm grad} \;p\;d{\bf s} &=&-\int {\rm rot}\left( \frac{1}{\rho}{\rm grad} \;p\right)d{\bf F}\\ &\uparrow&\\ &\text{Stokes-tétel}&\\ &=&-\int\left({\rm grad} \;\frac{1}{\rho}\times {\rm grad} \;p\right)d{\bf F}\\ &=&\int\frac{{\rm grad} \;\rho\times {\rm grad} \;p}{\rho^2}d{\bf F}\\ &=&\int{\bf B}d{\bf F} \end{eqnarray}$ ${\bf B}=\frac{{\rm grad} \;\rho\times {\rm grad} \;p}{\rho^2}$ : baroklin vektor.

Alkalmazások

• Nyugalomban levő légkörben nagy kiterjedésű felmelegedés lokálisan $\rightarrow$ nincs termodinamikai egyensúly, $s=\text{állandó}\quad \rightarrow$ baroklin.
  $\begin{eqnarray}\Downarrow\end{eqnarray}$
  Áramlás indul meg, ami általában örvényes lesz.
  • Egyenlítői erősebb felmelegedés $\rightarrow$ passzát (északi féltekén) - antipasszát
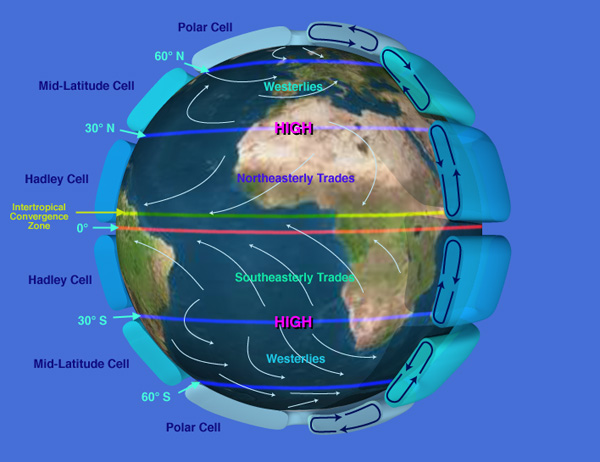
  • Óceán és szárazföld különböző mértékű felmelegedése télen és nyáron: monszun (évszakonként változó)
  • Szárazföld és víz különböző mértékű felmelegedése ill. lehűlése nappal és éjjel
  • Egyenlítői ciklonok: helyi felmelegedés (anticiklon: helyi lehűlés)
• Tengeri áramlás a sókoncentráció-különbség hatására
  $\rho$ növekszik a sótartalommal: alul áramlik a sósabb víz, felül a kevésbé sós
  • Áramlás Gibraltárnál: a Földközi-tenger sósabb, mint az Atlanti-óceán
  • Áramlás a Boszporusznál: a Földközi-tenger sósabb, mint a Fekete-tenger
• Nemkonzervatív erő (ugyanakkor barotróp folyadék)
  A legtipikusabb eset: Coriolis-erő
  Áramlás forgó koordináta-rendszerben
  Az Euler-egyenlet: $$\frac{d{\bf v}}{dt}=-{\rm grad}\; V-\frac{1}{\rho}{\rm grad}\;p\underbrace{-{\rm grad}\;\frac{\Omega_0^2R^2}{2}}_{\text{centrifugális gyorsulás}}\underbrace{-2\left({\bf \Omega_0}\times {\bf v}\right)}_{\text{Coriolis-gyorsulás}}$$ Bernoulli-egyenlet: $${\bf v}{\rm grad}\left(\frac{v^2}{2}+V-\frac{1}{2}\Omega_0^2R^2+w\right)=0$$ A cirkuláció egyenlete: $$\frac{d\Gamma}{dt}=-2\oint\left({\bf \Omega_0}\times {\bf v}\right)d{\bf s}$$ Szemléletes jelentése:
  Legyen $C$ jobbkéz-körüljárású. Ekkor $$\oint_C\left({\bf \Omega_0}\times {\bf v}\right)d{\bf s}={\bf \Omega_0}\oint_C\left({\bf v}\times d{\bf s}\right)={\bf \Omega_0}\oint_{C_\perp}\left({\bf v}_\perp\times d{\bf s}_\perp\right)$$ mivel ${\bf v}_\perp\times d{\bf s}_\perp$ a ${\bf v}\times d{\bf s}$ vektornak az ${\bf \Omega_0}$-lal párhuzamos komponense.
  $dt\left|{\bf v}_\perp\times d{\bf s}_\perp\right|$ a paralelogramma területe
  $\left|\oint ({\bf v}_\perp\times d{\bf s}_\perp)\right|$ a területváltozás $C_\perp^{t+dt}$ és $C_\perp^{t}$ között egységnyi idő alatt. $$\oint\left({\bf \Omega_0}\times {\bf v}\right)d{\bf s}=\Omega_0\frac{d\Sigma}{dt}\;,$$ ahol $\Sigma$ a $C_\perp$ által körbezárt terület.
  Passzát: A $C$ görbe az egyenlítő irányába mozog, $\frac{d\Sigma}{dt} < 0$, így $\Gamma_C$ növekszik $\Rightarrow$ erősödő áramlás keletről. (Antipasszát ugyanígy)
  Ciklon: az alsó légtömegek a mag felé áramlanak, $\frac{d\Sigma}{dt} < 0$, így $\Gamma_C$ növekszik: balra csavarodó áramvonalak. Ez összhangban van azzal, hogy a $2{\bf v}\times {\bf \omega}$ Coriolis-erő az északi féltekén jobbra, a déli féltekén balra térít el.
  
• Általános esetben mindkét oka megvan a cirkuláció megváltozásának. $$\frac{d\Gamma}{dt}=-2\oint\left({\bf \Omega_0}\times {\bf v}\right)d{\bf s}+\int{\bf B}d{\bf F}$$