


Áramlások fizikája
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
7. Előadás
7.1. Ismétlés
-
Örvénytételek
- Általánosan érvényes: az örvénycsőbe zárt örvényfluxus adott időpontban a
cső mentén állandó
$$K=\int {\bf \Omega}d{\bf F}=\text{állandó a cső mentén}$$
- Ideális, barotróp folyadékra konzervatív erőtér esetén érvényes
örvénytételek:
- Az örvénycsőbe zárt örvényfluxus időben sem változik.
- Ideális folyadékban örvények nem keletkeznek és nem szűnnek meg.
- Örvénycsövet alkotó folyadékrészek később is örvénycsövet alkotnak.
- Örvények keletkezése ideális folyadékban
Oka: baroklin (nem barotróp) folyadék és/vagy nem konzervatív erőtér (Coriolis erő)
$$\frac{d\Gamma_{C}}{dt}=\int{\bf B}d{\bf F}-2\Omega_0\frac{d\Sigma}{dt}$$
Itt
$${\bf B}=\frac{{\rm grad} \;\rho\times {\rm grad} \;p}{\rho^2}$$
a baroklin vektor,
$\Sigma$ pedig a $C$ görbének a ${\bf \Omega}_0$ szögsebesség-vektorra
merőleges vetülete által határolt terület.
- Alkalmazások:
- Helyi felmelegedés okozta örvények (Hadley-cellák, monszun)
- Sókoncentráció-különbség okozta örvényesség (Gibraltár, Boszporusz)
- A Föld forgása miatt fellépő örvényesség (passzátszél, ciklonok)

7.2. Örvényes áramlás összenyomhatatlan folyadékban
-
$\rho=\text{konst.}\quad \Rightarrow$ barotróp folyadék.
Ha még az erőtér is konzervatív, megmarad a cirkuláció. Az örvénycsövek időben
állandó örvényfluxusukkal jellemezhetők.
A feladat: ${\bf \Omega}$ adott, ${\bf v}=?$
- Egyenletek:
$$\text{div}\;{\bf v}=0$$
$$\frac{1}{2}\text{rot}\;{\bf v}={\bf \Omega}$$
- analógia a megnetosztatikával (kvázistacionárius áramok mágneses tere):
$$\text{div}\;{\bf B}=0$$
$$\text{rot}\;{\bf B}=\mu_0{\bf j}$$
- Integrális alak:
$$\oint {\bf v}\;d{\bf s}=2\kappa\equiv 2\int
{\bf \Omega}\;d{\bf F}$$
magnetosztatikai megfelelője:
$$\oint {\bf B}\;d{\bf s}=\mu_0 I=\mu_0 \int {\bf j}\;d{\bf F}$$
-
Általános megoldás:
vektorpotenciál:
$${\bf v}=\text{rot}\;{\bf A}$$
kiegészítő feltétel:
$$ \text{div}\;{\bf A}=0$$
Ekkor
$$\text{rot}\;{\bf v}=\text{rot}\;\text{rot}\;{\bf A}=\text{drad}\;\text{div}\;{\bf A}-\triangle\;{\bf A}=-\triangle\;{\bf A}$$
Ezzel a következő Poisson-egyenlethez jutunk:
$$\triangle\;{\bf A}=-2{\bf \Omega}$$
Ha ${\bf \Omega}$ a végtelenben eltűnik, akkor a megoldás
$${\bf A}({\bf r})=\frac{1}{4\pi}\int\frac{2{\bf \Omega}({\bf r}')}{\left|{\bf r}-{\bf r}'\right|}dV'$$
-
Örvényfonal körül:
$${\bf A}({\bf r})=\frac{\kappa}{2\pi}\int\frac{d{\bf s}'}{\left|{\bf r}-{\bf r}'\right|}$$
Ebből a sebességtér:
$${\bf v}({\bf r})=\frac{\kappa}{2\pi}\int\frac{d{\bf s}'\times
({\bf r}-{\bf r}')}{\left|{\bf r}-{\bf r}'\right|^3}$$
mint a magnetosztatikai Biot-Savart-törvény.
-
Alkalmazások
- Végtelen hosszú, egyenes örvényfonál
Kívül: örvénymentes áramlás
Az áramvonalak koncentrikus körök
$$\oint {\bf v}d{\bf s}=v_\varphi 2\pi r = 2\kappa\quad\Rightarrow\quad v_\varphi=\frac{\kappa}{\pi}\frac{1}{r}\;,\;v_r=0$$
Síkbeli áramlás, az $r=0$ vonaltól eltekintve örvénymentes.
Komplex potenciál:
$$w=\frac{\kappa}{\pi i}\ln z$$
$$\kappa=\Gamma/2$$
Komplex sebesség:
$$\frac{dw}{dz}=v_x-i v_y=\frac{\kappa}{\pi i}\frac{1}{z}$$
$r\rightarrow 0$-ra nem értelmes, viszont véges vastagságú örvénycső sebességtere
is ilyen az örvénycsövön kívül.
Ha az örvényfonál a $z_0=x_0+i y_0$ pontban van:
$$w=\frac{\kappa}{\pi i}\ln (z-z_0)$$
- Két párhuzamos, egyenes örvényfonál
$$w=\frac{\kappa_1}{\pi i}\ln (z-z_1)+\frac{\kappa_2}{\pi i}\ln (z-z_2)$$
Az örvényfonál a folyadékkal együtt mozog (örvénytétel) $\Rightarrow$ az adott örvény helyváltozását a többi örvényfonál sebességtere határozza meg.
- Két örvény mozgása
$\begin{eqnarray}
\frac{dx_1}{dt}-i\frac{dy_1}{dt}\equiv \frac{dz_1^*}{dt}&=&\frac{\kappa_2}{\pi i}\frac{1}{z_1-z_2}\quad\text{és}\quad\frac{dz_2^*}{dt}&=&\frac{\kappa_1}{\pi i}\frac{1}{z_2-z_1}\\
&\uparrow&\\
&\text{sodródás}&
\end{eqnarray}$
$$\Downarrow$$
$$\kappa_1\frac{dz_1^*}{dt}+\kappa_2\frac{dz_2^*}{dt}=0\;,\text{azaz}\quad
\kappa_1 z_1^*+\kappa_2 z_2^*=\text{állandó}$$
Mivel $\kappa_1$ és $\kappa_2$ valós,
$$\kappa_1 z_1+\kappa_2 z_2=\text{állandó}=(\kappa_1 +\kappa_2)z_c$$
$z_c$: örvényközéppont, analóg a tömegközépponttal. (Csak akkor értelmezzük, ha $\kappa_1 \ne -\kappa_2$.)
Az örvényközéppont nyugalomban van. A két örvény a középpont körül körmozgást végez:
$$v_{x1}=\frac{\kappa_2}{\pi}\frac{y_2-y_1}{(x_1-x_2)^2+(y_1-y_2)^2}$$
$$v_{y1}=-\frac{\kappa_2}{\pi}\frac{x_2-x_1}{(x_1-x_2)^2+(y_1-y_2)^2}$$
Ugyanis, mint látható, a sebesség merőleges az örvényeket összekötő ${\bf r}=(x_2-x1,y_2-y_1)$ szakaszra.
Ha $\kappa_1 +\kappa_2=0$, az örvényközéppont a végtelenben van, az örvénypár pedig egyenesvonalú egyenes mozgást végez az őket összekötő szakaszra merőleges irányban.
- Négy örvény mozgása
- Örvénygyűrűk
Füstkarika


Füstkarikák
Két örvénygyűrű ütközése
- Örvénysor (örvénylánc)
Tekintsük a következő komplex potenciált:
$$w=\frac{\kappa}{\pi i}\ln\left(\sin\left(\frac{\pi}{l}z\right)\right)$$
Ha $z\rightarrow n l\;,\quad n=0,\pm 1,\pm 2,\dots$,
$$w=\frac{\kappa}{\pi i}\ln\underbrace{\left[\sin\left(\pi n+\frac{\pi}{l}(z-nl)\right)\right]}_{(-1)^n\sin \frac{\pi}{l}(z-nl)\approx (-1)^n\frac{\pi}{l}(z-nl)}\rightarrow \frac{\kappa}{\pi i}\ln(z-n l)+\text{konst.}$$
Ez örvényfonál a $z_n=n l$ pontban $\kappa$ örvényfluxussal.
$w$ örvénysort ír le.
A komplex sebesség
$$\frac{dw}{dz}=\frac{\kappa}{l i}\text{ctg}\left(\frac{\pi}{l}z\right)
=\frac{\kappa}{l}\frac{-\text{ctg}\left(\frac{\pi}{l}x\right)\text{cth}\left(\frac{\pi}{l}y\right)+i}{\text{ctg}\left(\frac{\pi}{l}x\right)-i\text{cth}\left(\frac{\pi}{l}y\right)}=\underbrace{-\frac{\kappa}{l}\frac{\text{cth}\left(\frac{\pi}{l}y\right)\left(1+\text{ctg}^2\left(\frac{\pi}{l}x\right)\right)}{\text{ctg}^2\left(\frac{\pi}{l}x\right)+\text{cth}^2\left(\frac{\pi}{l}y\right)}}_{v_x}-i\underbrace{\frac{\kappa}{l}\frac{\text{ctg}\left(\frac{\pi}{l}x\right)\left(\text{cth}^2\left(\frac{\pi}{l}y\right)-1\right)}{\text{ctg}^2\left(\frac{\pi}{l}x\right)+\text{cth}^2\left(\frac{\pi}{l}y\right)}}_{v_y}$$
$y=0$-ra $v_x=0$, tehát az örvénysor nem mozog, stacionárius alakzat (de nem stabil).
Áramlási függvény:
$$\Psi=-\frac{\kappa}{\pi}\text{Re}\ln\left(\sin\left(\frac{\pi}{l}z\right)\right)=-\frac{\kappa}{\pi}\ln\left[\sin^2\left(\frac{\pi}{l}x\right)\text{ch}^2\left(\frac{\pi}{l}y\right)+\cos^2\left(\frac{\pi}{l}x\right)\text{sh}^2\left(\frac{\pi}{l}y\right)\right]^{1/2}=-\frac{\kappa}{2\pi}\ln\left[\sin^2\left(\frac{\pi}{l}x\right)+\text{sh}^2\left(\frac{\pi}{l}y\right)\right]$$
Áramvonalak:
$$\sin^2\left(\frac{\pi}{l}x\right)+\text{sh}^2\left(\frac{\pi}{l}y\right)=C$$
Zártak, amíg $C < 1$
Nyitottak, ha $C > 1$
A határgörbe (szeparátrix): $C=1$
$$\left|\cos\left(\frac{\pi}{l}x\right)\right|=\left|\text{sh}\left(\frac{\pi}{l}y\right)\right|$$
Az örvénysortól végtelen távol a sebesség $x$ irányú és
$$v_x(y=\pm \infty)=\mp \frac{\kappa}{l}$$
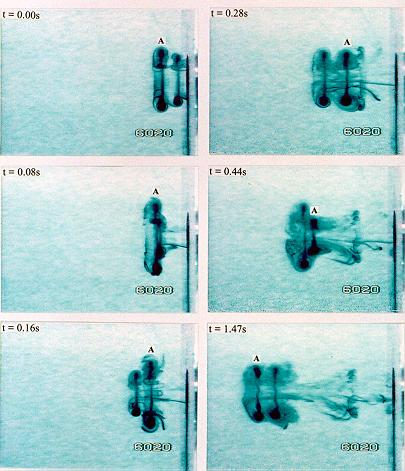
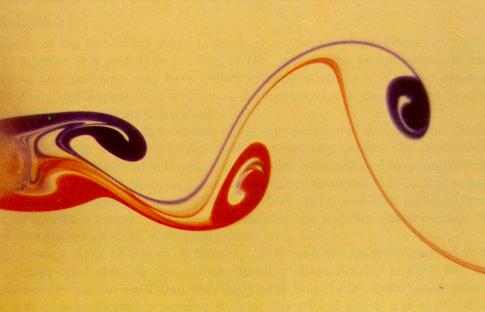
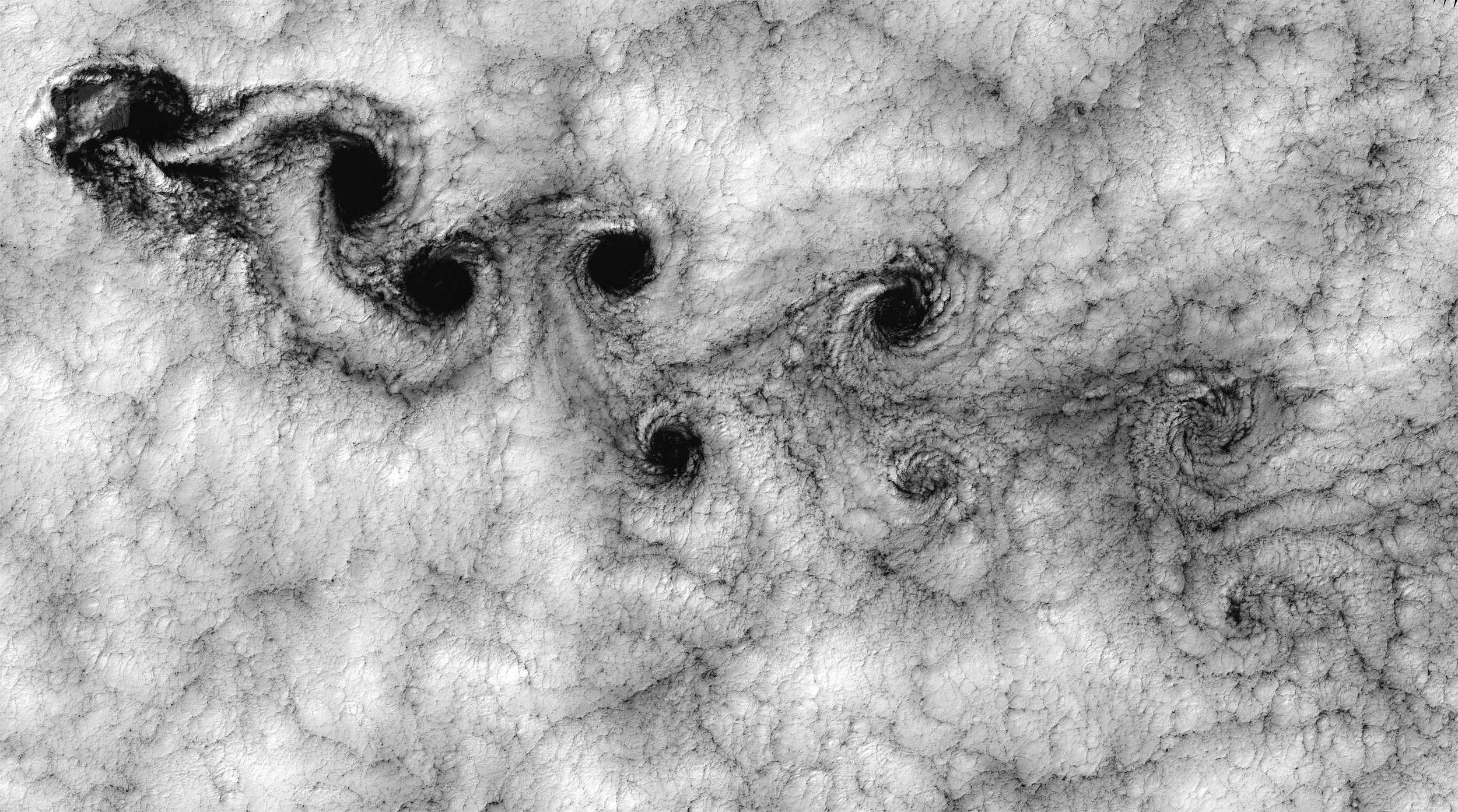
- Kármán-féle örvényút
Két $l/2$-vel eltolt, ellenkező irányban forgó örvénysor.
Önmagában egyik örvénylánc sem mozogna. Együtt $-x$ irányban eltolódik mindkettő. A sebesség
$$v=-\frac{\kappa}{l}\text{th}\left(\frac{\pi}{l}c\right)$$
ahol $c$ a két örvénylánc távolsága.
Hasonló alakzat képződik a folyadékban mozgó tárgyak mögött. Van olyan $c/l$ arány, melyre az örvényút stabil.
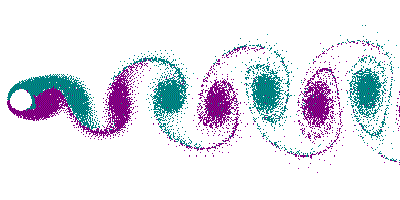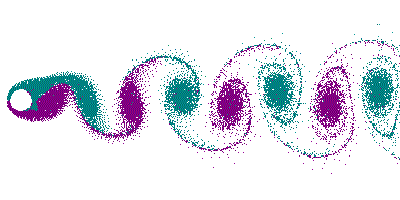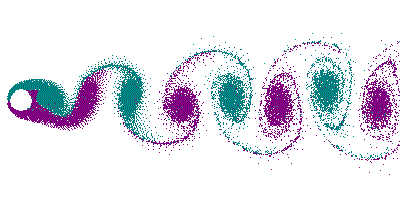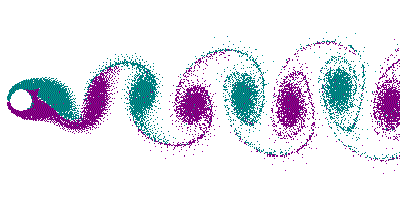
.jpg)
- Örvényréteg
Az örvényeket sűrítjük egy egyenes mentén ($x$-tengely), $l\rightarrow 0$ úgy, hogy az egységnyi hosszra es örvényesség állandó legyen:
$\kappa/l=\text{konst.}$.
Sebességtér: integrális alak:
$$\oint {\bf v}d{\bf s}=2\kappa$$
${\bf v}$ párhuzamos az egyenessel, emiatt
$$2Lv=2\frac{\kappa}{l} L\quad\rightarrow\quad v=\frac{\kappa}{l}$$
Az örvényréteg érintőleges szakadási felületet képez (az sebesség az örvényrétegen átlépve előjelet vált). Nem stabil. V.ö.: ciklon keletkezés.


 Gyula Bene 2008-02-14
Gyula Bene 2008-02-14



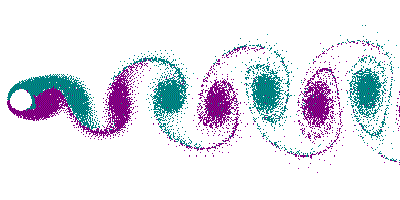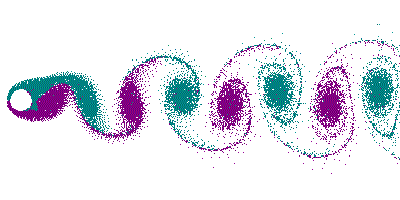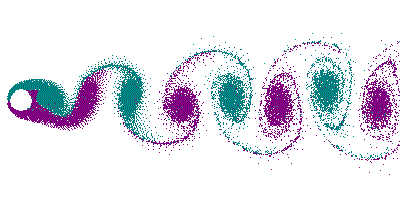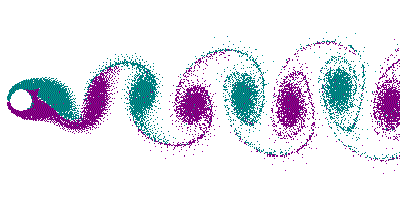

.jpg)