Hidrodinamika

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
9. Előadás
Sajátrezgések, állóhullámok. Sípok. Téglatest sajátrezgései. Nehézségi hullámok. Lineáris vízhullámok. Hullámtörés. Diszperzió. Hajóhullámok. Kapilláris hullámok. Nemlineáris hullámok sekély vízben.

9.1. Ismétlés

• Hullámok ideális folyadékban. Hanghullámok
  $ \begin{eqnarray} \frac{\partial^2 \rho'}{\partial t^2}-c^2\triangle\rho'=0\;,\quad c^2=\left(\frac{\partial p}{\partial \rho}\right)_s=\frac{1}{\rho_0\kappa_s} \end{eqnarray} $ $ \begin{eqnarray} \frac{\partial^2 p'}{\partial t^2}-c^2\triangle p'=0 \end{eqnarray} $ $$\frac{\partial^2 {\bf v}}{\partial t^2}-c^2\triangle {\bf v}=0$$
• Síkhullámok. A $+x$ irányban haladó hullám $$\Phi=f(x-ct)$$
  Monokromatikus síkhullám: $$\Phi=\text{Re}\left(A\text{e}^{i({\bf k}{\bf r}-\omega t)}\right)\;,\quad {\bf k}=\frac{\omega}{c}{\bf n}$$ $$c=\nu\lambda\;,\quad \omega=kc$$
• Hangterjedés mozgó közegben $$\omega=\omega'\left(1+\frac{u}{c}\cos\theta\right)$$
• Mozgó hangforrás nyugvó közegben $$\omega=\frac{\omega_0}{1-\frac{u}{c}\cos\theta}$$
• Az áramlás összenyomhatatlannak tekinthető, ha $$v\ll c$$
• Hangkeltés $\begin{eqnarray} \Phi( {\bf r} ,t)=-\frac{\dot{{\bf P}} \left(t-\frac{r}{c}\right) {\bf n} }{cr} \end{eqnarray}$ és $${\bf v}=\text{grad}\; \Phi=\frac{\ddot{ {\bf P}}\left(t-\frac{r}{c}\right){\bf n}}{c^2r}{\bf n}$$ Energiaáram-sűrűség: $cE{\bf n}$, ahol síkhullámra $E=\rho_0v^2$.
  A kisugárzott intenzitás $$I=\int c\rho_0\underbrace{\overline{v^2}}_{\text{időátlag}}{\bf n}d{\bf F}=\frac{4\pi\rho_0}{3c^3}\overline{\ddot P^2}$$
• Hangterjedés
  • A hőmérséklet, és ezzel együtt $c$ felfelé növekszik: Teljes visszaverődés, nagy távolságban hallani a hangot.
  • A hőmérséklet, és ezzel együtt $c$ felfelé csökken: A hang nem hallható.
  • A magas hangok messziről nem hallhatók (erősebb a csillapodásuk).
• Visszaverődés és törés $$\vartheta=\vartheta'$$ $$\frac{\sin\vartheta''}{\sin\vartheta}=\frac{c_2}{c_1}$$ $\vartheta$ : beesési szög, $\vartheta'$ : visszaverődési szög, $\vartheta''$ : törési szög.

9.2. Sajátrezgések, állóhullámok.
Külső erő hatása nélkül végbemenő szabad rezgések véges edényben. A határfeltételek miatt frekvenciájuk nem tetszőleges $\rightarrow$ sajátrezgések (végtelen sok módus lehetséges)
Állóhullámok alakulnak ki $$\Phi=\Phi_0({\bf r})\cos \omega t\;,$$ ahol $$\triangle \Phi_0+\frac{\omega^2}{c^2}\Phi_0=0\quad \text{+ határfeltételek}$$ A határfeltételek meghatározzák $\omega$-t is. A megoldások szuperpozíciója is megoldás (linearitás).

• Sípok.
  • Vékony, zárt cső (zárt nyelvsíp)
    A cső hossza legyen $L$, vastagsága elhanyagolható. $$\left.v_x\right|_{x=0}=\frac{\partial \Phi_0}{\partial x}=0\quad\quad\quad \left.v_x\right|_{x=L}=\frac{\partial \Phi_0}{\partial x}=0$$ $$\Phi_0''(x)=-\frac{\omega^2}{c^2}\Phi_0(x)\quad\rightarrow\quad \Phi_0(x)=A\cos\left(\frac{\omega}{c}x\right)+B\sin\left(\frac{\omega}{c}x\right)$$ $$\Phi_0'(0)=0\;\rightarrow \;B=0\quad\quad\quad \Phi_0'(0)=0=-A\frac{\omega}{c}\sin\left(\frac{\omega}{c}x\right)$$ $$\Downarrow$$ $$\Phi_0(x)=A\cos\left(\frac{\omega_n}{c}x\right)\quad\quad\quad \frac{\omega_n}{c}L=\pi n\;n=1,2,\ldots$$
    Sajátfrekvencia: $$\omega_n=\pi\frac{c}{L}n\quad\nu_n=\frac{c}{2L}n\quad \lambda_n=\frac{c}{\nu_n}$$ $$v_x(x)=-\underbrace{A\frac{\pi}{L}n}_{v_{x max}}\sin\left(\frac{\pi}{L}nx\right)\cos \omega_n t$$ $$p'(x)=-\rho_0\frac{\partial \Phi}{\partial t}=\rho_0\omega_n A\cos\left(\frac{\pi}{L}nx\right)\sin \omega_n t$$
    Ahol $v_x$ maximális, ott $p$ minimális (v.ö. Bernoulli-tétel), ellentétes rezgés. $$p'(x)\propto \rho'(x)$$
    Ugyanilyen képletek érvényesek a megfeszített húr rezgéseire. Ott a rezgés transzverzális, tehát $z \ne 0$ és $c=\sqrt{\frac{\sigma}{\rho}}$.
    ezzel a kezdeti kitéréssel $$z=A_1\sin\left(\frac{\pi}{L}x\right)\cos\left(\pi\frac{c}{L}t\right)+ A_2\sin\left(2\frac{\pi}{L}x\right)\cos\left(2\pi\frac{c}{L}t\right)$$ Csak az alaphang és oktávja szólal meg.
    Minden felhang megszólal (különböző intenzitással).
    A zárt cső mint rezonátor előfordul az orgona nyelvsípjai között.
    
    A kialakuló hullámok

    $n=1$	$\nu_1=\frac{c}{2L}$	alaphang ($c^1$)
    $n=2$	$\nu_2=\frac{c}{L}$	oktáv ($c^2$)
    $n=3$	$\nu_3=\frac{3}{2}\frac{c}{L}$	(tiszta) kvint 3:2 ($g^2$)
    $n=4$	$\nu_4=2\frac{c}{L}$	oktáv ($c^3$)
    $n=5$	$\nu_5=\frac{5}{2}\frac{c}{L}$	(nagy) terc 5:4 ($e^3$)
    $n=6$	$\nu_6=3\frac{c}{L}$	kvint 3:2 ($g^3$)
    $n=7$	$\nu_7=\frac{7}{2}\frac{c}{L}$	kis szeptim 7:4 ($b^3$)
    $n=8$	$\nu_8=4\frac{c}{L}$	oktáv ($c^4$)

    
    Az általános megoldás $$v_x(x,t)=\sum_{n=1}^\infty A_n\sin\left(\frac{\pi}{L}n x\right)\cos\left(\pi\frac{c}{L}n t\right)$$ Fourier-sor. Az $A_n$ együtthatókat a kezdeti feltételek határozzák meg.
    A hangszínt az amplitudó-eloszlás $\{A_n\}$ adja meg. (Pl.: üveghang, ha a páratlan felharmonikusokat kizárjuk.)
  • Nyitott nyelvsíp
    
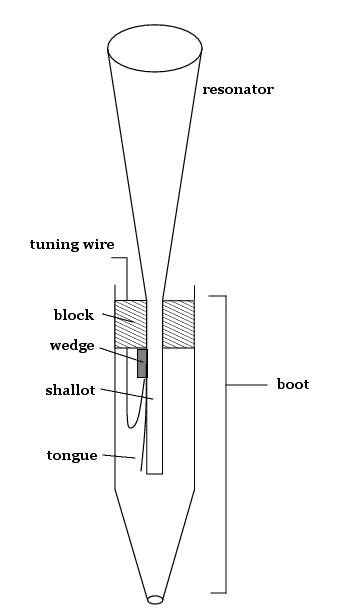
    A tetején ($x=L$) $p=$áll., tehát $p'$ csomópontja, azaz $v_x$ maximuma. Az alaphang ezért $\lambda_1=4L$ hullámhosszú, $\nu_1=\frac{c}{4L}$ frekvenciájú (mélyebb, mint a zártnál).
    A következő felhang csak $\lambda_2=\frac{4}{3}L$ hullámhosszú lehet, $\nu_2=\frac{3}{4}\frac{c}{L}$, tehát csak a páratlan felhangok jelennek meg. $$\nu_{n'}=\frac{c}{4L}n'\;,\;n'=1,3,5,\ldots$$
  • Ajaksípok
    
    
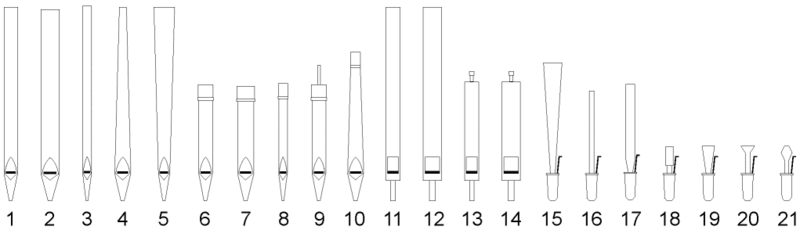
    Erősen fújva alul maximális a sebesség (pl. orgona).
    Nyitott eset: $$\nu_n=\frac{c}{2L}n\;,\;n=1,2,3,\ldots$$
    Zárt eset: $$\nu_{n'}=\frac{c}{4L}n'\;,\;n'=1,3,5,\ldots$$
    Blockflöte gyengén fújva, mint nyelvsíp:
    alaphangja: $\nu=\frac{c}{4L}\approx \frac{330}{4\cdot 0.3}=225 Hz$ (valójában $c^1=264 Hz$)
    Erősen fújva, mint ajaksíp. Az alt (f) és szoprán blockflöte csövének hosszaránya $\approx 1.5$.
• Téglatest sajátrezgései.
  $v_n=0$ a falakon.
  Egyetlen állóhullám: $$\Phi({\bf r},t)=A\cos\left(\frac{\pi}{L_1}lx\right)\cos\left(\frac{\pi}{L_2}my\right)\cos\left(\frac{\pi}{L_3}nz\right)$$ $$\Downarrow$$ $$\omega^2=c^2\pi^2\left(\frac{l^2}{L_1^2}+\frac{m^2}{L_2^2}+\frac{n^2}{L_3^2}\right)$$ $l,m,n$ egész számok. Mindegyik számhármas meghatároz egy sajátfrekvenciát. Ezek sorozata sokkal bonyolultabb, mint a felhangoké.
  Egy általános rezonátordobozbeli megoldás $$\Phi({\bf r},t)=\sum_{i=1}^\infty A_i \Phi_{i0}({\bf r})\cos(\omega_i t+\alpha_i)$$ Itt $\alpha_i$-k az egyes rezgési módusok kezdeti fázisai.
  $\omega_i$ diszkrét, de szabálytalan értékeket vehet fel.
  A hangszer hangszíne a rezonátorban kialakuló sajátrezgésektől és azok amplitudóeloszlásától $\{A_i\}$ függ.
  Rezonátor: hegedűtest, cső.

9.4. Nehézségi hullámok (vízhullámok).

Véges mélységű folyadékban
Feltesszük, hogy $y$-tól nem függ semmi (széles medence)
Összenyomhatatlan folyadékot vizsgálunk
Feltesszük, hogy az áramlás örvénymentes: ${\bf v}=\text{grad}\;\Phi$
Alapegyenletek: $$\triangle \Phi=0$$ $$\frac{\partial \Phi}{\partial t}+\frac{1}{2}\left(\text{grad}\;\Phi\right)^2+\frac{p-p_0}{\rho_0}+gz=0$$ Bernoulli-egyenlet, $p_0$ az atmoszférikus nyomás.
Peremfeltételek:
A felület egyenlete $z=\zeta(x,t)$

• A felületi sebesség $\zeta$ változásából adódik
  Egy részecske sebessége közvetlenül a felület alatt $$\dot z=\frac{d\zeta}{dt}=\frac{\partial \zeta}{\partial t}+v_x\frac{\partial \zeta}{\partial x}$$ $$\Downarrow$$ $$\left.\frac{\partial \Phi}{\partial z}\right|_\zeta=\frac{\partial \zeta}{\partial t}+v_x\frac{\partial \zeta}{\partial x}$$
• A nyomás $\zeta$-nál $p_0$: $$\left.\left(\frac{\partial \Phi}{\partial t}+\frac{1}{2}\left(\text{grad}\;\Phi\right)^2+gz\right)\right|_\zeta=0$$
• Alul nincs $z$ irányú sebesség: $$\left.\frac{\partial \Phi}{\partial z}\right|_{z=-h}=0$$

9.5. Lineáris vízhullámok.
Ha $v$ és $\zeta$ kicsi, akkor a négyzetes tagok a lineárisak mellett elhagyhatók:
Egyenletek: $$\triangle \Phi=0$$ $$\frac{\partial \Phi}{\partial t}+\frac{p-p_0}{\rho_0}+gz=0$$
Peremfeltételek:

• $$\left.\frac{\partial \Phi}{\partial z}\right|_\zeta=\frac{\partial \zeta}{\partial t}=\dot z$$
• $$\left.\left(\frac{\partial \Phi}{\partial t}+gz\right)\right|_\zeta=0$$
• A fenti két peremfeltételből következik, hogy $$\left.\left(\frac{\partial^2 \Phi}{\partial t^2}+g\frac{\partial \Phi}{\partial z}\right)\right|_\zeta=0$$
• $$\left.\frac{\partial \Phi}{\partial z}\right|_{z=-h}=0$$

pozitív irányba haladó hullámot keresünk. Feltevés: $$\Phi(x,z,t)=\Phi_0(x-ct)\chi(z)$$ $$\triangle \Phi=0\quad\Rightarrow\quad \Phi_0''\chi+\Phi_0\chi''=0$$ $$\frac{\Phi_0''}{\Phi_0}=-\frac{\chi''}{\chi}$$
A baloldal csak $x-ct$-től, a jobboldal csak $z$-től függ, ezért mindkettő konstans kell hogy legyen: $$\Phi_0''=-k^2\Phi_0\quad\quad\quad\chi''=k^2\chi$$
$c$ függhet $k$-tól!
Megoldás: $$\Phi_0(x-ct)=A_1\cos(kx-\underbrace{kc(k)}_{\equiv \omega(k)}t)\;,\quad \chi(z)=A\;\text{ch}k(z+h)+B\;\text{sh}k(z+h)$$
$k$ a hullámszám.
Az utolsó peremfeltétel miatt $B=0$.
Tehát $$\Phi(x,z,t)=A\cos(kx-kct)\;\text{ch}k(z+h)$$
Az utolsóelőtti peremfeltételből $$\omega^2 A\;\text{ch}k(\zeta +h)=gkA\;\text{sh}k(\zeta +h)$$
Mivel $\zeta\ll h$ gyenge zavar esetén, $$\omega^2=gk\;\text{th}kh$$ azaz $$\omega=\sqrt{gk\;\text{th}kh}$$
A körfrekvencia és a hullámszám között nemlineáris a kapcsolat $\rightarrow$ diszperzió: a terjedési sebesség függ a hullámhossztól.
A második határfeltételből a hullámfelület: $$\zeta(x,t)=\left.-\frac{1}{g}\frac{\partial \Phi}{\partial t}\right|_{\zeta\approx 0}=\frac{A\omega}{g}\;\text{ch}kh \sin(kx-\omega t)$$
A diszperzió következményei

• Fázissebesség és csoportsebesség
  
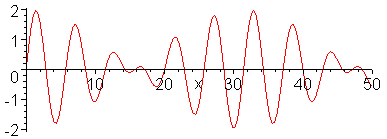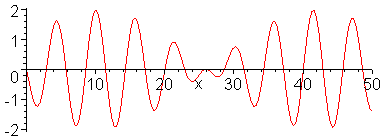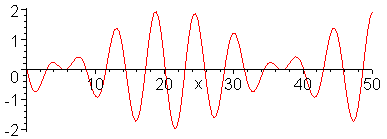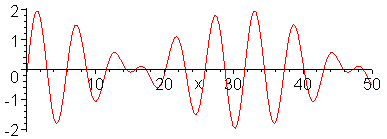
  Fázissebesség: $$c=\frac{\omega(k)}{k}$$
  Csoportsebesség: $$c_g=\frac{d \omega(k)}{d k}$$ A csoportsebesség jelentése: $$\zeta(x,t)=\int dk f(k) {\rm e}^{i(kx-\omega(k)t)}$$ A hullámhegyek és hullámvölgyek azok a helyek, ahol az interferencia erős, vagyis a fázis csak lassan változik a hullámszám függvényében. Ennek feltétele: $$\frac{\partial}{\partial k}\left(kx-\omega(k)t\right)=0$$ azaz $$x=\frac{d \omega(k)}{d k}t$$ A hullámhegyek és hullámvölgyek tehát a csoportsebességgel mozognak.
  
  Lineáris vízhullámok esetén a fázissebesség $$c=\sqrt{\frac{g}{k}\;\text{th}kh}\;,$$ a csoportsebesség $$c_g=\frac{1}{2}\sqrt{\frac{g}{k}\;\text{th}kh}+\frac{h}{2}\sqrt{\frac{g k }{\text{sh}kh\;\text{ch}^3 kh}}=\frac{1}{4}\sqrt{\frac{g\left(\text{sh}^2(2kh)+(2kh)^2\right)}{k\;\text{sh}kh\;\text{ch}^3 kh}}\;.$$ Határesetek:
  • mély víz: $$\lambda=\frac{2\pi}{k}\ll h\quad \rightarrow \quad kh\gg 1\;,\quad \text{th}kh\approx 1$$ $$\omega(k)=\sqrt{gk}$$ Fázissebesség: $$c=\sqrt{\frac{g}{k}}$$ Csoportsebesség: $$c_g=\frac{1}{2}\sqrt{\frac{g}{k}}=\frac{c}{2}$$
  • sekély víz: $$\lambda=\frac{2\pi}{k}\gg h\quad \rightarrow \quad kh\ll 1\;,\quad \text{th}kh\approx kh$$ $$\omega(k)=\sqrt{gh}k$$ Nincs diszperzió, a fázissebesség egyenlő a csoportsebességgel: $$c=c_g=\sqrt{gh}$$
• Szétfolyás
  Legyen a kezdeti hullámalak $\sigma$ félszélességű haranggörbe (Gauss-függvény): $$\zeta(x,0)=A\exp\left(-\frac{x^2}{2\sigma^2}\right)=\text{Re }\frac{A\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty {\rm e}^{-\frac{\sigma^2}{2}k^2}{\rm e}^{ikx}dk$$ Ekkor $$\zeta(x,t)=\text{Re }\frac{A\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty {\rm e}^{-\frac{\sigma^2}{2}k^2}{\rm e}^{i(kx-\omega(k)t)}dk$$ Ha $$\omega(k)\approx \left.\frac{d\omega(k)}{dk}\right|_{k=0}k+\frac{1}{2}\left.\frac{d^2\omega(k)}{dk^2}\right|_{k=0}k^2=ak+\frac{1}{2}bk^2\;,$$ akkor $$\zeta(x,t)=\text{Re }\frac{A\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty {\rm e}^{-\frac{\sigma^2+ibt}{2}k^2}{\rm e}^{ik(x-at)}dk=\text{Re }A\sqrt{\frac{\sigma^2}{\sigma^2+ibt}}\exp\left(-\frac{(x-at)^2}{2(\sigma^2+ibt)}\right)=A\sqrt[4]{\frac{\sigma^4}{\sigma^4+b^2t^2}}\exp\left(-\frac{(x-at)^2}{2(\sigma^2+b^2t^2/\sigma^2)}\right)\cos\left(\frac{(x-at)^2bt}{2(\sigma^4+b^2t^2)}+\delta\right)$$ Ennek burkolója $\sqrt{\sigma^2+b^2t^2/\sigma^2}>\sigma$ félszélességű haranggörbe (melynek maximuma az $x=at$ helyen van).
  A szétfolyás oka: az egyes monokromatikus összetevők különböző sebességgel haladnak, így az idő múlásával egyre inkább rendezetlen fázisokkal adódnak össze. $\rightarrow$ Az amplitudó csökken, a szélesség növekszik.
• Hullámtörés
  
  $\lambda > h$ esetén $c=\sqrt{gh}$, ezért a mélyebb vízben terjedő hullámok gyorsabbak, utolérik a sekélyebb vízben terjedőket és átbuknak rajtuk.
  
  Cunami (szökőár), 2004, Thaiföld. A tengerrengés okozta hullámok a nyílt óceánon többszáz kilométer hullámhosszúságúak és mindössze kb. 300mm-es amplitudójúak. Partközelben lelassulnak, feltorlódnak (4-30 méteres magasságú vízfallá), és az addig nagy területen szétoszló energiájuk a partszakaszokon koncentrálódva hatalmas pusztítást okoz.
• Kelvin-féle hajóhullámok
  
  
  
  
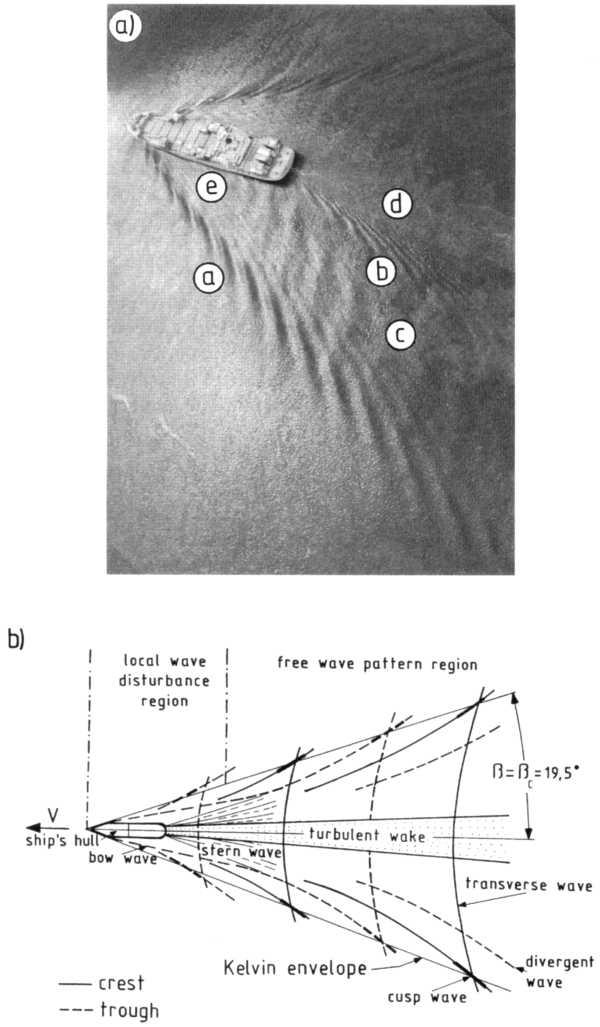
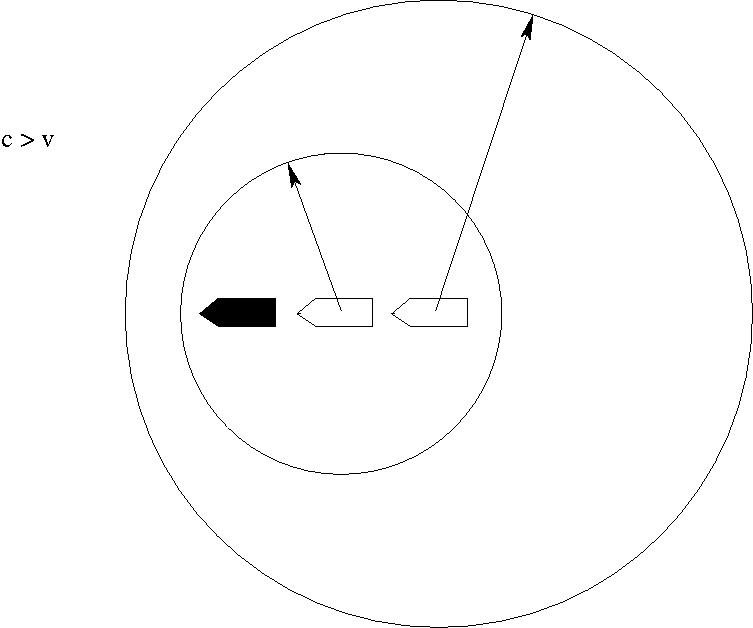
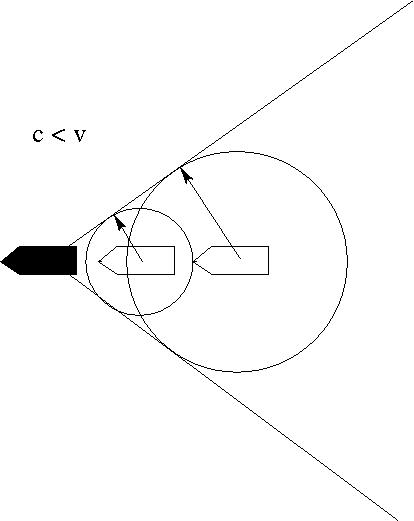
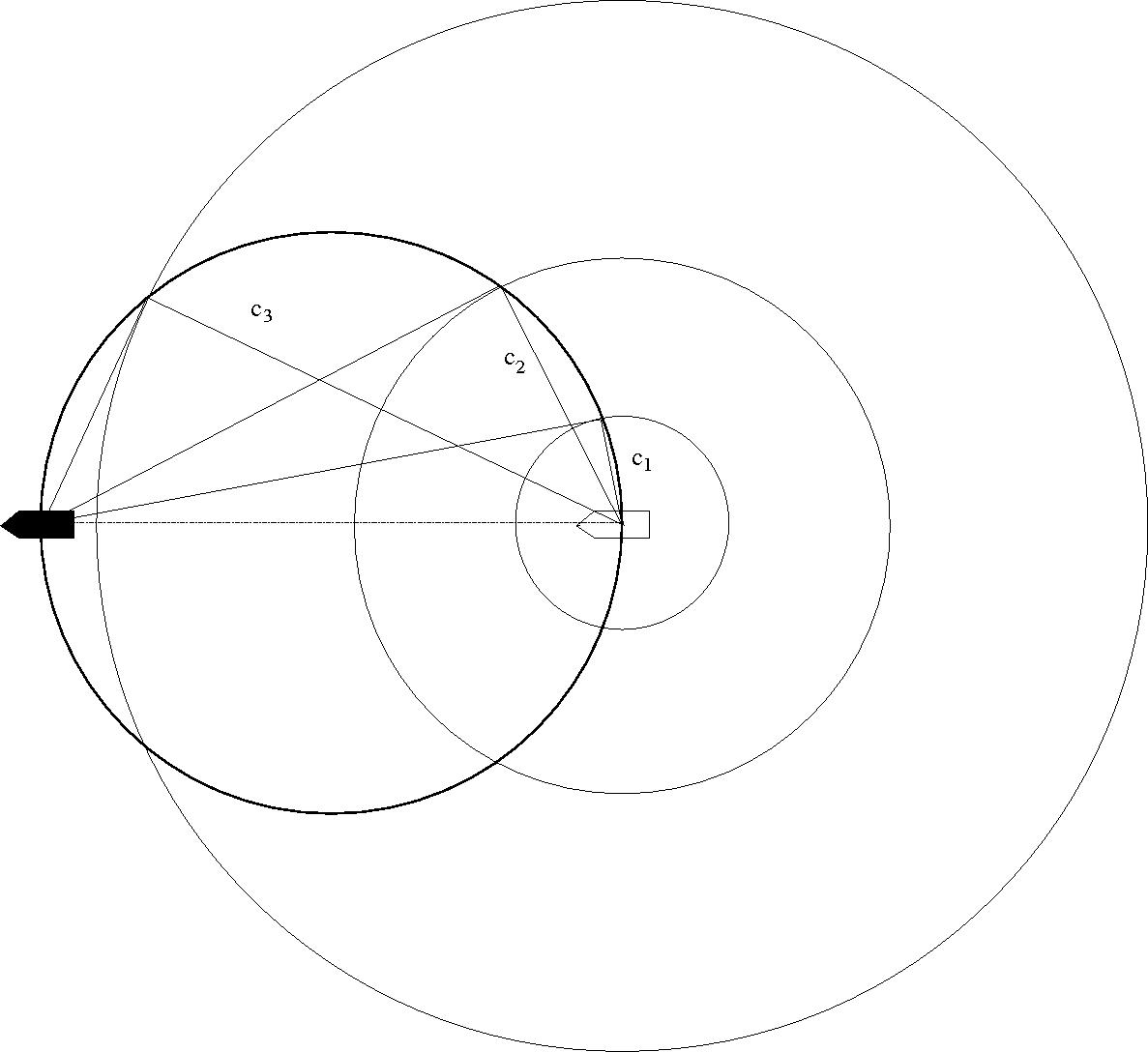
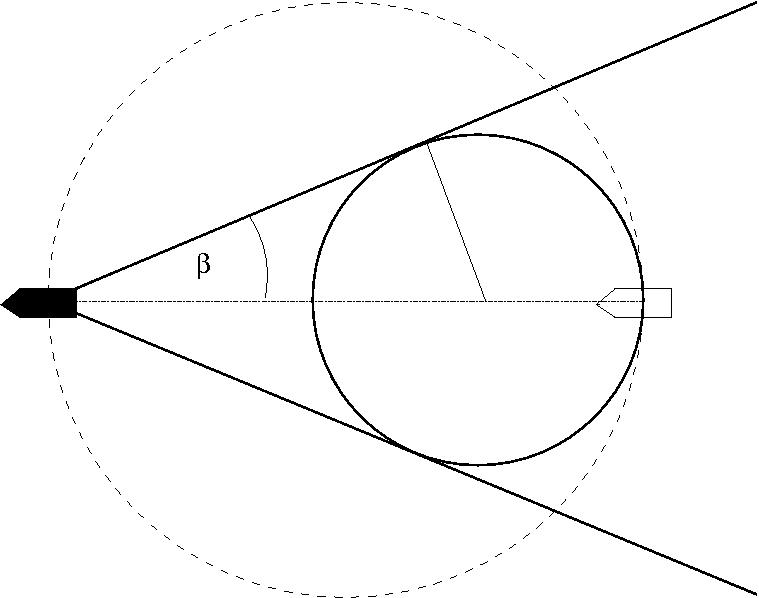
  $$\sin \beta= \frac{1}{3}\quad \Rightarrow \quad \beta = 19^\circ 28'$$
  
  Hajóhullámok a felhőzetben. A hajó szerepét itt az Amszterdam-sziget játssza (Indiai-óceán)
  
  William Thomson (Lord Kelvin), (1824-1907)

9.6. Kapilláris hullámok.

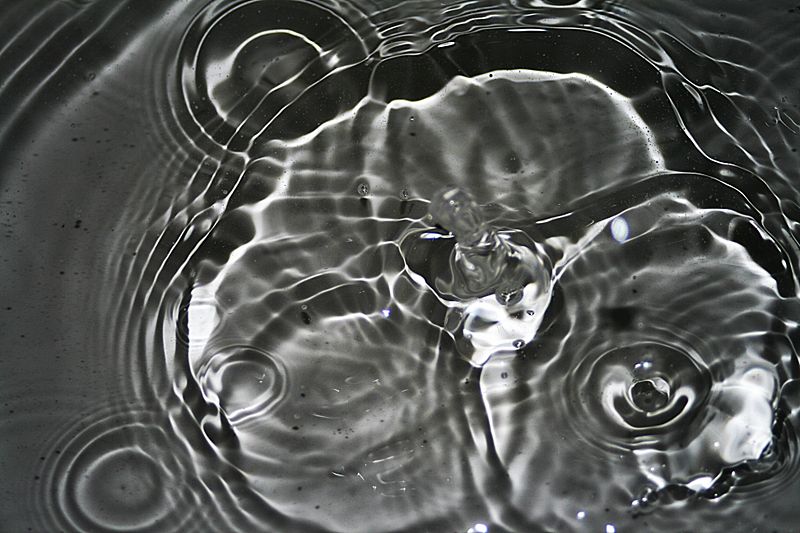
Esőcseppek becsapódása által keltett kapilláris hullámok

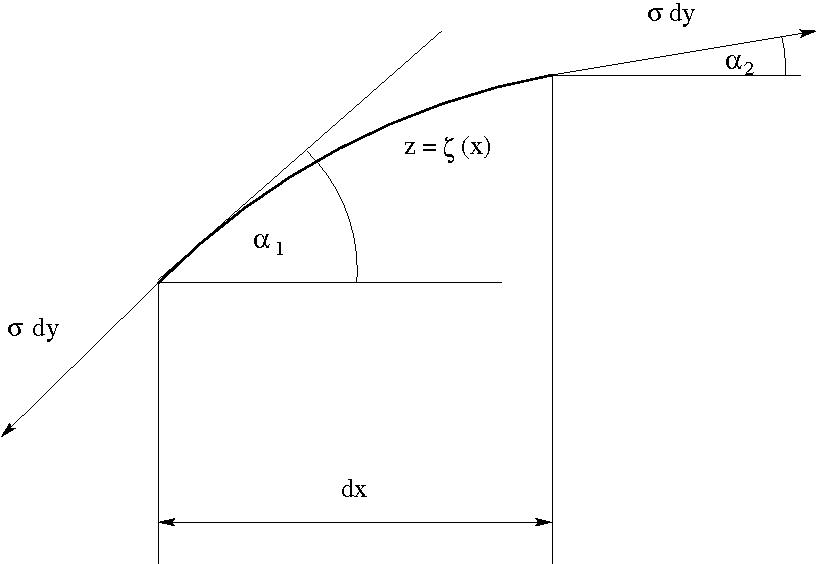
A felületi feszültségből eredő nyomás: $$ \Delta p=\frac{\sigma dy (\alpha_1-\alpha_2)}{dy\;dx/\cos \alpha_1}=-\sigma \frac{\zeta''}{\left(1+\zeta'^2\right)^{\frac{3}{2}}} $$ Lineáris vízhullámok esetén a egyenletek: $$\triangle \Phi=0$$ $$\frac{\partial \Phi}{\partial t}+\frac{p+\Delta p-p_0}{\rho}+gz=0$$
Peremfeltételek:

• $$\left.\frac{\partial \Phi}{\partial z}\right|_\zeta=\frac{\partial \zeta}{\partial t}=\dot z$$
• $$\left.\frac{\partial \Phi}{\partial t}\right|_\zeta+g\zeta-\frac{\sigma}{\rho}\zeta''=0$$
• A fenti két peremfeltételből következik, hogy $$\left.\left(\frac{\partial^2 \Phi}{\partial t^2}+g\frac{\partial \Phi}{\partial z}-\frac{\sigma}{\rho}\frac{\partial^3 \Phi}{\partial z\partial x^2}\right)\right|_\zeta=0$$
• $$\left.\frac{\partial \Phi}{\partial z}\right|_{z=-h}=0$$

A megoldás ismét $$\Phi(x,z,t)=A\cos(kx-\omega t)\;{\rm ch}\;k(z+h)$$ Ezt a felszínen felírt Bernoulli-egyenletbe betéve: $$-\omega^2 \;{\rm ch}\;k(\zeta +h)+gk\;{\rm sh}\;k(\zeta +h)+\frac{\sigma}{\rho}k^3\;{\rm sh}\;k(\zeta +h)=0$$ Mivel $\zeta\ll h$, azt kapjuk, hogy $$ \omega(k)=\sqrt{\left(gk+\frac{\sigma}{\rho}k^3\right){\rm th}\;kh} $$
Kapilláris hullámok mély víz felszínén: $$\omega(k)=\sqrt{gk+\frac{\sigma}{\rho}k^3}$$
Itt $\sigma$ a felületi feszültség.

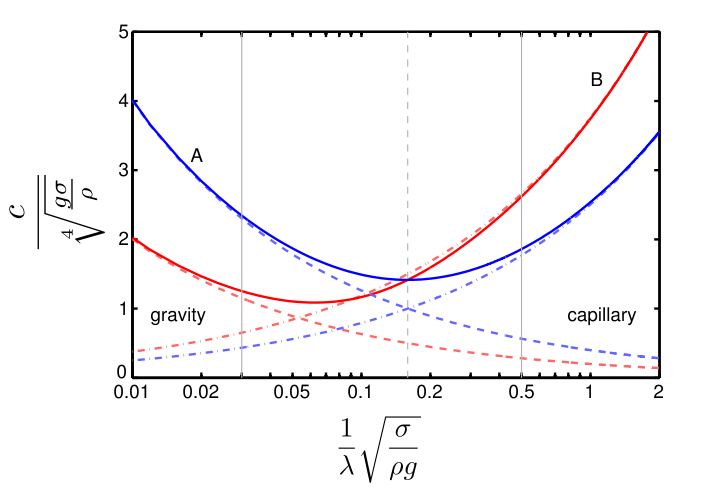
Kapilláris hullámok fázis- és csoportsebessége a hullámszám függvényében. Fázissebesség: kék, csoportsebesség: piros

Fázissebesség: $$c(k)=\sqrt{\frac{g}{k}+\frac{\sigma}{\rho}k}$$
Csoportsebesség: $$c_g(k)=\frac{g+3\frac{\sigma}{\rho}k^2}{2\sqrt{gk+\frac{\sigma}{\rho}k^3}}=\frac{3}{2}c(k)-\frac{g/k}{c(k)}$$

9.7. Nemlineáris hullámok sekély vízben.
A Korteweg-de Vries-egyenlet $$\frac{\partial \zeta}{\partial t}+c\left(\frac{\partial \zeta}{\partial x}+\frac{3}{2h}\zeta\frac{\partial \zeta}{\partial x}+\frac{h^2}{6}\frac{\partial^3 \zeta}{\partial x^3}\right)=0$$
Itt $c=\sqrt{gh}$.
Szoliton $$\zeta(x,t)=\underbrace{\frac{v_0^2-c^2}{g}}_{A \text{ amplitudó}}\frac{1}{\text{ch}^2\left[\sqrt{\frac{3}{4}\frac{v_0^2-c^2}{c^2h^2}}(x-v_0t)\right]}$$ Ez a nemlinearitás miatt megőrzi alakját, nem folyik szét. $$v_0^2=g(h+A)$$
A sebesség az amplitudótól függ, és nagyobb a lineáris hullámok maximális $c=\sqrt{gh}$ sebességénél (bár csak kicsivel, mivel $v_0\approx c\left(1+\frac{1}{2}\frac{A}{h}\right)$ és $A\ll h$ ).

A szoliton felfedezése: John Scott Russell, 1834.

Csónak megállása után vízdomb, kb. 14 km/h-val halad, szélessége ~7 m, magassága ~0.4 m. A vízmélység 1.1 m volt. Negyedórán át tudta követni lóháton.
Későbbi kísérletek. A legjobb keltési mód: kő vízbeejtése.


A nagyobb szoliton utoléri és megelőzi a kisebbet. A szolitonok ütközéskor megőrzik alakjukat.