Kváziperiodikus út

Next: Káosz konzervatív rendszerekben Up: További káoszhoz vezető utak Previous: Intermittencia

Kváziperiodikus út

Hopf-bifurkáció: a kontrollparaméter változásakor egy fixpont elveszti a stabilitását és helyette egy (róla leváló) stabil határciklus jelenik meg.
Példa (két dimenzió, polárkoordináták):

$\begin{displaymath}\frac{dr}{dt}=-\left(\Gamma\; r+r^3\right)\end{displaymath}$

$\begin{displaymath}\frac{d\theta}{dt}=\omega\end{displaymath}$

Itt $\Gamma =a-a_c$ , a kontrollparaméter, a kontrollparaméter kritikus értéke.
Megoldás:

$\begin{displaymath}r^2(t)=\frac{\Gamma\; r_0^2\; {\rm e}^{-2\Gamma t}} {r_0^2 \left(1-{\rm e}^{-2\Gamma t}\right)+\Gamma}\end{displaymath}$

$\begin{displaymath}\theta(t)=\omega t\end{displaymath}$

Kezdeti feltételek:

$\begin{displaymath}r(t=0)=r_0\end{displaymath}$

$\begin{displaymath}\theta(t=0)=0\end{displaymath}$

Stabilitásvizsgálat:
Áttérünk Descartes-koordinátákra:

$\begin{displaymath}\frac{dx}{dt}=-\left(\Gamma\; +(x^2+y^2)\right)x-y\omega\end{displaymath}$

$\begin{displaymath}\frac{dy}{dt}=-\left(\Gamma\; +(x^2+y^2)\right)y+x\omega\end{displaymath}$

Linearizálunk az origó körül:

$\begin{displaymath}\frac{d{\bm r}}{dt}={\bm A}{\bm r}\end{displaymath}$

ahol ${\bm r}=(x,y)$ és

$\begin{displaymath}{\bm A}= \left(\begin{array}{cc} -\Gamma &-\omega\\ \omega &-\Gamma \end{array}\right)\end{displaymath}$

sajátértékek:

$\begin{displaymath}\lambda_\pm=-\Gamma\pm i\omega\end{displaymath}$

$\Longrightarrow$ Hopf-bifurkáció esetén egy konjugált komplex sajátérték-pár lépi át a képzetes tengelyt.
Landau turbulencia-elmélete:
a kontrollparaméter (Reynolds-szám) növelésekor az egymást követő Hopf-bifurkációk során egyre bonyolultabb kváziperiodikus mozgás alakul ki. A turbulencia a nagyon nagy számú független frekvencia esetét jelenti.
A káoszhoz vezető Ruelle-Takens-Newhouse-út:
a kontrollparaméter (Reynolds-szám) növelésekor két egymást követő Hopf-bifurkáció után tipikusan különös attraktoron való kaotikus mozgás jelenik meg.
Kísérleti bizonyítékok: Bénard-instabilitás (Dubois és Bergé, 1982), Taylor-instabilitás (Brandstätter et.al., 1983).
A kváziperiodikus út modellje és univerzális tulajdonságai: a kör-leképezés

$\begin{displaymath}\theta_{n+1}=\theta_{n}+\Omega-\frac{K}{2\pi}\sin(2\pi \theta_{n})\end{displaymath}$

vagy általánosabban:

$\begin{displaymath}\theta_{n+1}=f_{\Omega,K}(\theta_{n})\end{displaymath}$

ahol
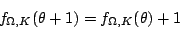
- $\begin{displaymath}f_{\Omega,K}(\theta+1)=f_{\Omega,K}(\theta)+1\end{displaymath}$
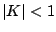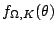- $\vert K\vert<1$ esetén $f_{\Omega,K}(\theta)$ invertálható és inverzével együtt differenciálható
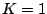- esetén 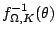$f_{\Omega,K}^{-1}(\theta)$ nem differenciálható
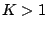- esetén 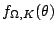$f_{\Omega,K}(\theta)$ nem invertálható
Két paraméter van, többféle átmenet lehetséges.
Csavarási szám:

$\begin{displaymath}w=\lim_{n\rightarrow \infty} \frac{f_{\Omega,K}^n(\theta_0)-\theta_0}{n}\end{displaymath}$

Kváziperiodikus viselkedés $\equiv$ irracionális csavarási szám
Univerzális tulajdonságokat találunk, ha adott $K\le 1$ esetén olyan $\Omega_{p,q}$ értékeken keresztül tartunk $\Omega^*$ -hoz, melyekre a csavarási számok az irracionális csavarási szám lánctört-közelítései. Kikötjük továbbá, hogy a 0 is a periodikus pontok egyike, azaz

$\begin{displaymath}f_{\Omega_{p,q}K}^q(0)=p\end{displaymath}$

Legyen pl. (``aranymetszés''). Ekkor a lánctört-kifejtés

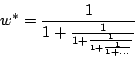
$\begin{displaymath}w^*=\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+...}}}}\end{displaymath}$

$\begin{displaymath}w^*=\frac{1}{1+w^*}\quad \Rightarrow\quad w^{*2}+w^*-1=0\end{displaymath}$

Véges lánctört-közelítés:

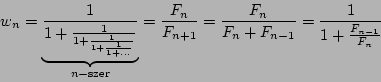
$\begin{displaymath}w_n=\underbrace{\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+.... ...{n+1}}= \frac{F_n}{F_n+F_{n-1}}=\frac{1}{1+\frac{F_{n-1}}{F_n}}\end{displaymath}$

Itt -ek a Fibonacci-számok:

$\begin{displaymath}F_{n+1}=F_n+F_{n-1}\quad ; F_0=0\quad ; F_1=1\quad ; n=0,\;1,\;2,\; ...\end{displaymath}$

Univerzalitás:
- A 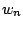-hez tartozó 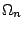$\Omega_n$ -re
  
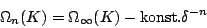
  $\begin{displaymath}\Omega_n(K)=\Omega_\infty(K)-{\rm konst.}\delta^{-n}\end{displaymath}$
  
  ahol
  
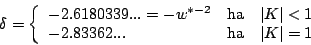
  $\begin{displaymath}\delta=\left\{ \begin{array}{lcl} -2.6180339...=-w^{*-2} & {\... ...1\\ -2.83362... & {\rm ha} & \vert K\vert=1 \end{array}\right.\end{displaymath}$
  
  Univerzális számok!
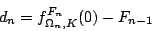
- $\begin{displaymath}d_n=f_{\Omega_n,K}^{F_n}(0)-F_{n-1}\end{displaymath}$
  
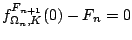  ( $f_{\Omega_n,K}^{F_{n+1}}(0)-F_{n}=0$ )
  
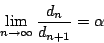
  $\begin{displaymath}\lim_{n\rightarrow \infty} \frac{d_n}{d_{n+1}}=\alpha\end{displaymath}$
  
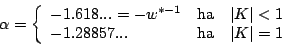
  $\begin{displaymath}\alpha=\left\{ \begin{array}{lcl} -1.618...=-w^{*-1} & {\rm h... ...1\\ -1.28857... & {\rm ha} & \vert K\vert=1 \end{array}\right.\end{displaymath}$
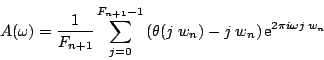
- $\begin{displaymath}A(\omega)=\frac{1}{F_{n+1}}\sum_{j=0}^{F_{n+1}-1} \left(\theta(j\;w_n)-j\;w_n\right){\rm e}^{2\pi i \omega j\;w_n}\end{displaymath}$
  
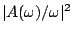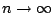  A teljesítményspektrum, $\vert A(\omega)/\omega\vert^2$ az $n\rightarrow \infty$ határesetben önhasonló.
Szinkronizáció, Arnold-nyelvek
Stabil racionális csavarási szám:

$\begin{displaymath}f_{\Omega,K}^q(\theta_i^*)=p+\theta_i^*\end{displaymath}$

$\begin{displaymath}\left\vert\prod_{i=1}^q f'_{\Omega,K}(\theta_i^*)\right\vert=... ...\prod_{i=1}^q \left[1-K\cos(2\pi\theta_i^*)\right]\right\vert<1\end{displaymath}$