


Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
2. hét csütörtöki előadás
Egyenes menti (egydimenziós) mozgások
Mozgásegyenlet:
$$m\ddot{x}=-\frac{dV}{dx}$$
Energia megmaradása (a mozgásegyenlet első integrálja):
$$E=\frac{m}{2}\dot{x}^2+V(x)={\rm állandó}$$
$$\Rightarrow\quad V(x)\le E$$
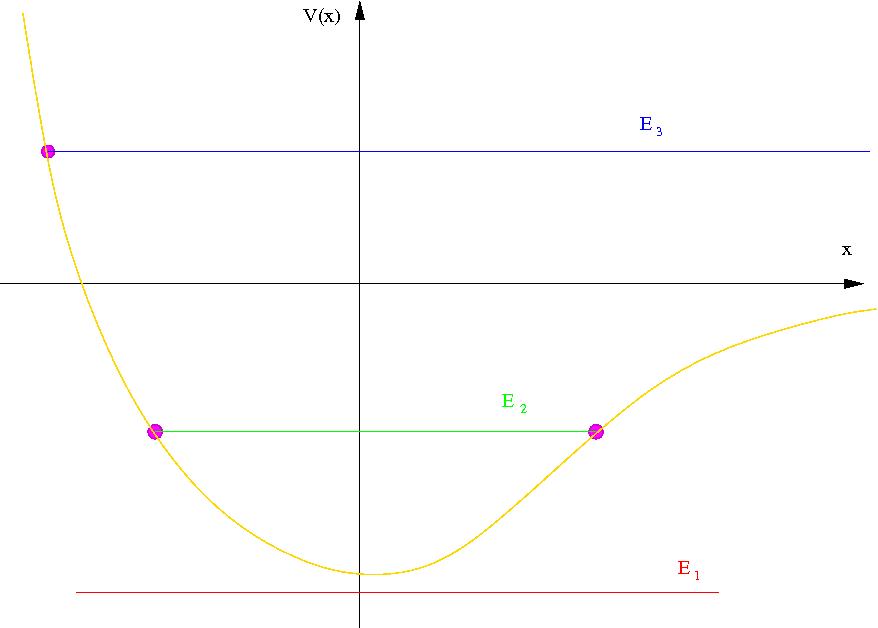
1. ábra. Tömegpont mozgása egydimenziós potenciálban. A
$E_1$ energiájú mozgás nem valósulhat meg, az
$E_2$ energiájú mozgás korlátos (két
fordulópont, lilával), az $E_3$ energiájú
mozgás félvégtelen (egy fordulópont).
$$\dot{x}=\pm \sqrt{\frac{2}{m}\left(E-V(x)\right)}$$
A két lehetséges előjel a mozgás megfordíthatóságát (időtükrözési szimmetria)
fejezi ki.
Változók szétválasztása:
$$dt=\frac{dx}{\sqrt{\frac{2}{m}\left(E-V(x)\right)}}$$
Integrálás:
$$t-t_0=\int_{x_0}^x\frac{dx}{\sqrt{\frac{2}{m}\left(E-V(x)\right)}}$$
Itt $t_0$ integrációs állandó.
Korlátos mozgás periódusideje:
$$T=2\int_{x_1}^{x_2}\frac{dx}{\sqrt{\frac{2}{m}\left(E-V(x)\right)}}=\sqrt{2m}\int_{x_1}^{x_2}\frac{dx}{\sqrt{E-V(x)}}$$
Harmonikus rezgőmozgás
$$F=-Dx\quad \Rightarrow \quad V(x)=\frac{1}{2}Dx^2$$
$$T=\sqrt{2m}\int_{x_1}^{x_2}\frac{dx}{\sqrt{E-\frac{1}{2}Dx^2}}=\sqrt{\frac{2m}{E}}\int_{x_1}^{x_2}\frac{dx}{\sqrt{1-\frac{D}{2E}x^2}}$$
Fordulópontok (v.ö. amplitudó):
$$x_{1,2}=\pm\sqrt{\frac{2E}{D}}$$
Új változó bevezetése:
$$\xi=\sqrt{\frac{D}{2E}}x$$
Ezzel
$$T=\sqrt{\frac{2m}{E}}\int_{-1}^{1}\frac{\sqrt{\frac{2E}{D}}d\xi}{\sqrt{1-\xi^2}}=2\sqrt{\frac{m}{D}}\int_{-1}^{1}\frac{d\xi}{\sqrt{1-\xi^2}}$$
Még egy új változó:
$$\xi=\sin\varphi$$
$$d\xi=\cos\varphi d\varphi$$
Ezzel
$$T=2\sqrt{\frac{m}{D}}\int_{-\pi/2}^{\pi/2}\frac{\cos\varphi
d\varphi}{\cos\varphi}=2\sqrt{\frac{m}{D}}\int_{-\pi/2}^{\pi/2}d\varphi=2\pi\sqrt{\frac{m}{D}}$$
$$\Rightarrow \quad \omega\equiv\frac{2\pi}{T}=\sqrt{\frac{D}{m}}\quad\Rightarrow
\quad D=m\omega^2$$
A mozgásegyenlet megoldása ($x(t)$ meghatározása):
$$t=t_0+\sqrt{\frac{m}{2E}}\int_{0}^{x}\frac{dx}{\sqrt{1-\frac{D}{2E}x^2}}$$
Változócserék (mint fent):
$$t=t_0+
\sqrt{\frac{m}{D}}\int_{0}^{x\sqrt{D/(2E)}}\frac{d\xi}{\sqrt{1-\xi^2}}$$
$$t=t_0+\sqrt{\frac{m}{D}}\int_{0}^{\arcsin\left(x\sqrt{D/(2E)}\right)}d\varphi$$
azaz
$$t=t_0+\sqrt{\frac{m}{D}}\arcsin\left(x\sqrt{\frac{D}{2E}}\right)$$
$$\Rightarrow
x=\sqrt{\frac{2E}{D}}\sin\left(\sqrt{\frac{D}{m}}(t-t_0)\right)=\sqrt{\frac{2E}{m\omega^2}}\sin\left(\omega(t-t_0)\right)=A\cos(\omega
t -\delta)$$
amplitudó:
$$A=\sqrt{\frac{2E}{m\omega^2}}$$
fázis:
$$\delta=\omega t_0+\frac{\pi}{2}$$
Az
$$\ddot{x}=-\omega^2 x$$
mozgásegyenlet általános megoldása:
$$x=a\cos\omega t +b\sin\omega t$$
ebből
$$\dot{x}=-a\omega\sin\omega t+b\omega\cos\omega t$$
Az $a$ és $b$ integrációs állandók a kezdeti $x_0$ hellyel és $v_0$
sebességgel fejezhetők ki, mivel $t=0$ esetén
$$x_0=a\;,\quad v_0=b\omega$$
Ezzel
$$x=x_0\cos\omega t +\frac{v_0}{\omega}\sin\omega t$$
ill.
$$\dot{x}=v_0\cos\omega t - x_0\omega\sin\omega t$$
Másrészt
$$x=A\cos(\omega t-\delta)=A\cos\delta\cos\omega t+A\sin\delta\sin\omega t$$
Tehát
$$A\cos\delta=x_0$$
és
$$A\sin\delta=\frac{v_0}{\omega}$$
Ebből
$$A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$$
és
$$\tan\delta=\frac{v_0}{x_0 \omega}$$
Mechanikai energia:
$$E=\frac{1}{2}m v_0^2+\frac{1}{2}m \omega^2 x_0^2$$
Csillapított harmonikus rezgőmozgás
$$m\ddot{x}=-Dx-k\dot{x}$$
vagy
$$\ddot{x}+2\alpha\dot{x}+\omega_0^2x=0$$
Itt $\alpha=\frac{k}{2m}$ és $\omega_0=\sqrt{\frac{D}{m}}$.
Keressük a megoldást exponenciális alakban, azaz tegyük fel, hogy
$$x=A{\rm e}^{\kappa t}$$
Azt kapjuk, hogy
$$\kappa^2+2\alpha\kappa+\omega_0^2=0$$
Tehát
$$\kappa=-\alpha\pm\sqrt{\alpha^2-\omega_0^2}$$
- $\quad\alpha>\omega_0\quad$: két valós, negatív gyök. Általános megoldás:
$$x(t)=A_1{\rm e}^{\kappa_1 t}+A_2{\rm e}^{\kappa_2 t}\equiv A_1{\rm
e}^{-|\kappa_1 |t}+A_2{\rm e}^{-|\kappa_2| t} $$
Túlcsillapított rezgések (pl. lengéscsillapító).
- $\quad\alpha<\omega_0\quad$: két negatív valós részű, konjugált komplex
gyök.
Mit jelent ez? Mivel
$${\rm e}^{ix}=\cos(x)+i\sin(x)\;,$$
ilyenkor
$$x(t)={\rm e}^{-\alpha t}\left(a\cos(\Omega t)+b\sin(\Omega
t)\right)\equiv A{\rm e}^{-\alpha t}\cos(\Omega t+\delta) $$
a megoldás. Itt
$$\Omega=\sqrt{\omega_0^2-\alpha^2}$$
Csillapított harmonikus rezgések.
- $\quad\alpha=\omega_0\quad$: két egyenlő, negatív gyök.
Megoldás:
$$x(t)=\lim_{\Omega\rightarrow 0}{\rm e}^{-\alpha t}\left(a\cos(\Omega t)+b\frac{\sin(\Omega
t)}{\Omega}\right)={\rm e}^{-\alpha t}\left(a+bt\right)$$


 bene@arpad.elte.hu
bene@arpad.elte.hu
