Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
3. hét keddi előadás
Kényszerrezgések, rezonancia
Mi történik, ha egy csillapított harmonikus oszcillátort periodikusan
gerjesztünk?
$$m\ddot{x}=-Dx-k\dot{x}+F\cos(\omega t)$$
avagy
$$\ddot{x}+2\alpha\dot{x}+\omega_0^2 x=f\cos(\omega t)$$
Itt $f=F/m$.
Komplex írásmód (a valós résznek van fizikai tartalma, de az egyenlet
linearitása miatt elég a számolás végén meghatározni a valós részt):
$$\ddot{x}+2\alpha\dot{x}+\omega_0^2 x=f{\rm e}^{i\omega t}$$
Egy partikuláris megoldás:
$$x=A{\rm e}^{i\omega t}$$
ahol $A$ ezúttal határozott értékű lesz, mivel
$$A\left(-\omega^2+2i\alpha\omega+\omega_0^2 \right)=f$$
Ebből
$$A=\frac{f}{\omega_0^2-\omega^2+2i\alpha\omega}=\frac{f}{\sqrt{\left(\omega_0^2-\omega^2\right)^2+4\alpha^2\omega^2}}{\rm
e}^{-i\delta}$$
ahol
$$\delta={\rm arctg}\left(\frac{2\alpha\omega}{\omega_0^2-\omega^2}\right)$$
Tehát
$$x=\frac{f}{\sqrt{\left(\omega_0^2-\omega^2\right)^2+4\alpha^2\omega^2}}
\cos(\omega t-\delta)$$
Kényszerrezgés.
Ehhez még a homogén egyenlet,
$$\ddot{x}+2\alpha\dot{x}+\omega_0^2 x=0$$
tetszőleges megoldása hozzáadható (tranziensek):
$$x=\frac{f}{\sqrt{\left(\omega_0^2-\omega^2\right)^2+4\alpha^2\omega^2}}
\cos(\omega t-\delta)+{\rm e}^{-\alpha t}\left(a\cos(\Omega t)+b\sin(\Omega
t)\right)$$
Megjegyzés: A tranziensek lehetnek túlcsillapított rezgések is.
A mozgás ábrázolása fázistérben
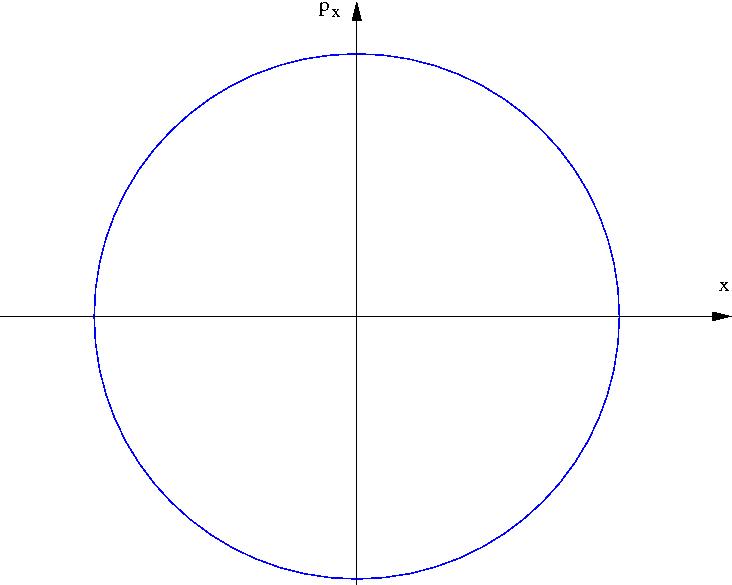
Harmonikus oszcillátor fázistrajektóriája (ellipszis)
$$E=\frac{m}{2}v_x^2+\frac{1}{2}m\omega^2x^2=\frac{p_x^2}{2m}+\frac{1}{2}m\omega^2x^2$$
$$\frac{p_x^2}{2mE}+\frac{x^2}{2E/(m \omega^2)}=1$$
Az ellipszis tengelyei $\sqrt{2mE}$ ill. $\sqrt{\frac{2E}{m \omega^2}}$ hosszúságúak.
A mozgásegyenletek numerikus megoldása
$$\ddot{x}=f(x,\dot{x})$$
Átalakítás elsőrendű egyenletrendszerré:
$\begin{eqnarray}
\dot{x}&=&v\\
\dot{v}&=&f(x,v,t)
\end{eqnarray}$
Explicit Euler-módszer:
$\begin{eqnarray}
t^{(n+1)}&=&t^{(n)}+dt\\
x^{(n+1)}&=&x^{(n)}+v^{(n)}dt\\
v^{(n+1)}&=&v^{(n)}+f(x^{(n)},v^{(n)},t^{(n)})dt
\end{eqnarray}$
A hiba $dt^2$ nagyságrendű.
Középpont-módszer (másodrendű Runge-Kutta):
$\begin{eqnarray}
t^{(n+1/2)}&=&t^{(n)}+dt/2\\
x^{(n+1/2)}&=&x^{(n)}+v^{(n)}dt/2\\
v^{(n+1/2)}&=&v^{(n)}+f(x^{(n)},v^{(n)},t^{(n)})dt/2\\
t^{(n+1)}&=&t^{(n)}+dt\\
x^{(n+1)}&=&x^{(n)}+v^{(n+1/2)}dt\\
v^{(n+1)}&=&v^{(n)}+f(x^{(n+1/2)},v^{(n+1/2)},t^{(n+1/2)})dt
\end{eqnarray}$
A hiba $dt^3$ nagyságrendű.
Alkalmazás kényszerrezgések esetére
Mozgás a fázistérben, Poincaré-metszet
Anharmonikus rezgések
Nagy kitéréseknél az erő nem marad lineáris függvénye a kitérésnek
$$F=-D x +\beta x^2 +\gamma x^3...$$
Mozgásegyenlet:
$$m\ddot{x}=-D x +\beta x^2+\gamma x^3$$
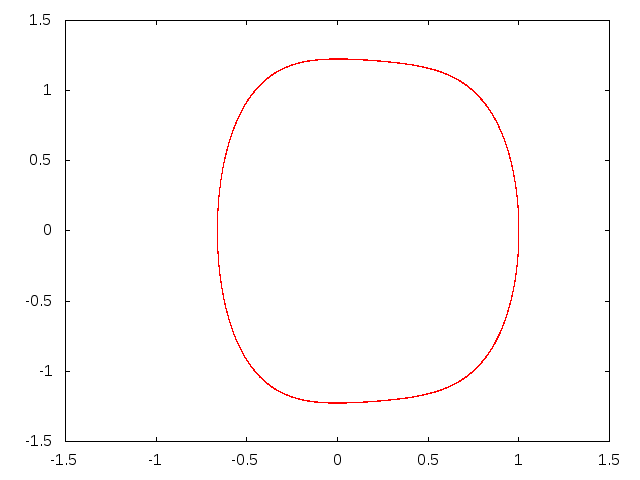Anharmonikus szabad rezgések (fázistér)
Csillapított anharmonikus rezgések:
$$m\ddot{x}=-D x +\beta x^2+\gamma x^3-k\dot{x}$$
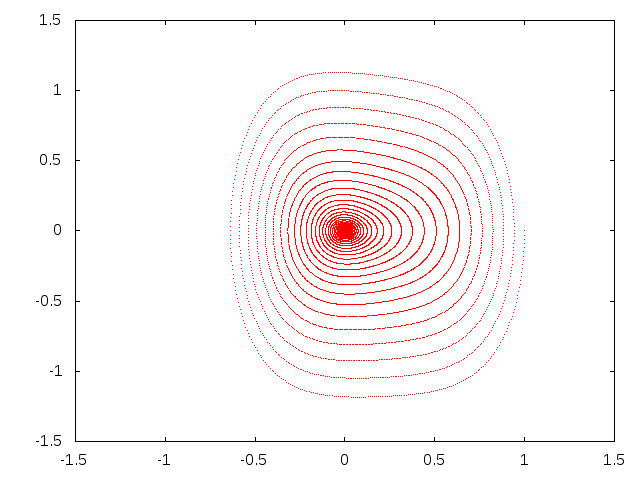Csillapított anharmonikus szabad rezgések (fázistér)
Anharmonikus kényszerrezgések periodikus gerjesztő erő esetén:
$$m\ddot{x}=-D x +\beta x^2+\gamma x^3+F\cos\omega t$$
Csillapított anharmonikus kényszerrezgések periodikus gerjesztő erő esetén:
$$m\ddot{x}=-D x +\beta x^2+\gamma x^3-k\dot{x}+F\cos\omega t$$
Kaotikus viselkedés, érzékenység a kezdeti
feltételekre, Ljapunov-exponensek
Egymásra merőleges harmonikus rezgések, Lissajous-görbék
Lissajous-görbék
bene@arpad.elte.hu