


Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
3. hét csütörtöki előadás
Ismétlés: egydimenziós mozgás,
rezgések
Kaotikus viselkedés, érzékenység a kezdeti
feltételekre, Ljapunov-exponensek, különös attraktor
Egymásra merőleges harmonikus rezgések, Lissajous-görbék
Térbeli mozgás
Az impulzusnyomaték fogalma, mozgásegyenlete
Impulzusnyomaték (impulzusmomentum, perdület)
$${\bf N}={\bf r}\times{\bf p}\equiv {\bf r}\times m{\bf v} $$
Mozgásegyenlete:
$$\dot{{\bf N}}=\dot{{\bf r}}\times{\bf p}+{\bf r}\times\dot{{\bf p}}={\bf
v}\times m{\bf v}+{\bf r}\times {\bf F}={\bf r}\times {\bf F}$$
Forgatónyomaték:
$${\bf M}={\bf r}\times {\bf F}$$
Ezzel
$${\bf M}=\frac{d {\bf N}}{dt}$$
Adott irányra vett vetület kiszámítása:
$${\bf n}\cdot{\bf N}={\bf n}\cdot\left({\bf r}\times{\bf p}\right)={\bf
p}\cdot\left({\bf n}\times{\bf r}\right)$$
Ugyanígy
$${\bf n}\cdot{\bf M}={\bf n}\cdot\left({\bf r}\times{\bf F}\right)={\bf
F}\cdot\left({\bf n}\times{\bf r}\right)$$
$\Rightarrow$ "Erő szorozva az erőkarral."
Konzervatív erőtér, adott ${\bf n}$ irány körüli forgásszimmetrikus potenciál:
$${\bf n}\cdot{\bf M}={\bf F}\cdot\left({\bf n}\times{\bf
r}\right)=-\left({\bf n}\times{\bf r}\right)\cdot {\bf \nabla}V$$
Mivel $\delta \varphi \left({\bf n}\times{\bf r}\right)$ az ${\bf r}$
helyvektor megváltozása az ${\bf n}$ tengely körüli $\delta \varphi$ szögű
elforgatás hatására, ${\bf n}\cdot{\bf M}$ arányos a potenciál elforgatás
miatti megváltozásával. Ha a potenciál forgásszimmetrikus, ${\bf n}\cdot{\bf
M}=0$, de akkor az impulzusmomentum dinamikai egyenlete szerint ${\bf
n}\cdot{\bf N}=0$, az impulzusmomentum forgástengellyel párhuzamos vetülete
megmarad. Az impulzusmomentum megmaradása a forgásszimmetria következménye.
Centrális erőterek
$$V({\bf r})=V(r)$$
A potenciál csak az erőtér centrumától mért távolságtól függ.
$$ {\bf F}=-{\bf \nabla}V=-\frac{dV}{dr}\frac{{\bf r}}{r}$$
Az erő a centrum felé (vagy azzal ellentétes irányba) mutat.
Példák:
$q$ ponttöltés potenciális energiája $Q$ ponttöltés terében (v.ö. Coulomb-potenciál)
$$V(r)=\frac{1}{4\pi \epsilon_0}\frac{qQ}{r}$$
$m$ tömegű anyagi pont potenciális energiája $M$ tömegű anyagi pont terében (v.ö. Newton-potenciál)
$$V(r)=-G\frac{mM}{r}$$
A tér centrumára vonatkozóan az impulzusmomentum minden komponense megmarad.
$\Rightarrow$ A mozgás síkmozgás, az impulzusmomentumra merőleges síkban zajlik.
Területi tétel (Kepler második törvénye): az erőtér centrumából a ponttömeghez húzott sugár egyenlő
idők alatt egyenlő területeket súrol.
$$dA=\frac{1}{2}r\cdot r d\varphi=\frac{1}{2}r^2 \dot{\varphi}dt$$
Mivel a kerületi sebesség $r \dot{\varphi}$, az impulzusmomentum nagysága
$$N=r\cdot mr\dot{\varphi}=mr^2\dot{\varphi}$$
Ebből
$$r^2\dot{\varphi}=\frac{N}{m}\;,$$
és így
$$\frac{dA}{dt}=\frac{1}{2}r^2 \dot{\varphi}=\frac{N}{2m}=\text{állandó}.$$
A területi tétel az impulzusmomentum megmaradásából következik és minden
centrális erőtérben érvényes.
Mozgás centrális erőterekben
$$N=mr^2\dot{\varphi}$$
$$E=\frac{m}{2}\left(\dot{r}^2+r^2\dot{\varphi}^2\right)+V(r)$$
$$E=\frac{m}{2}\dot{r}^2+\frac{N^2}{2m r^2}+V(r)$$
Centrifugális potenciál:
$$\frac{N^2}{2m r^2}$$
Effektív potenciál:
$$V_{eff}(r)=V(r)+\frac{N^2}{2m r^2}$$
$$E=\frac{m}{2}\dot{r}^2+V_{eff}(r)$$
$$\dot{r}=\pm \sqrt{\frac{2}{m}\left(E-V_{eff}(r)\right)}$$
$$t=t_0+\int\frac{dr}{\sqrt{\frac{2}{m}\left(E-V_{eff}(r)\right)}}$$
$$\dot{\varphi}=\frac{N}{mr^2}$$
$$\varphi=\varphi_0+\int\frac{\frac{N}{mr^2} dr}{\sqrt{\frac{2}{m}\left(E-V_{eff}(r)\right)}}$$
Mozgás tömegpont gravitációs terében
Feltéve, hogy $M\gg m$, a nagyobb tömegű test nem (helyesebben: csak elhanyagolható mértékben) mozdul el (ha a választott
inerciarendszerben kezdetben nyugalomban volt).
$$V(r)=-G\frac{mM}{r}$$
$$V_{eff}(r)=-G\frac{mM}{r}+\frac{N^2}{2m r^2}$$
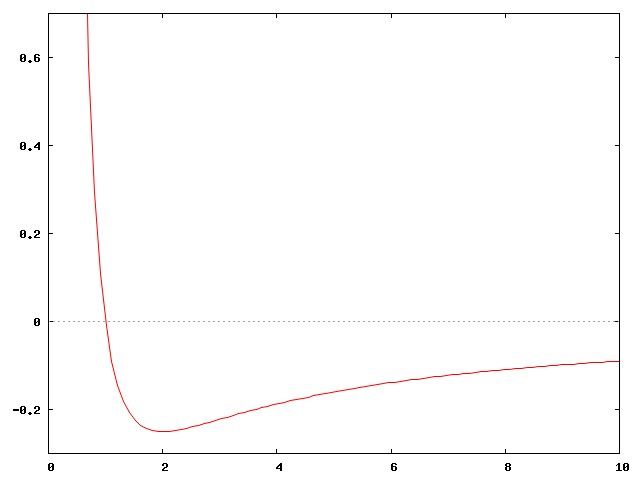
Effektív potenciál
A pálya fordulópontjai (bolygóknál napközel és naptávol):
$$E=\frac{N^2}{2mr^2}-G\frac{mM}{r}\equiv V_{eff}(r)$$
$$\xi=\frac{1}{r}$$
$$\xi^2-2\frac{Gm^2M}{N^2}\xi-\frac{2mE}{N^2}=0$$
$$\frac{1}{r_{1,2}}=\xi_{1,2}=\frac{Gm^2M}{N^2}\pm\sqrt{\left(\frac{Gm^2M}{N^2}\right)^2+\frac{2mE}{N^2}}$$
Ha $E\ge 0$, $\xi_2\le 0$. Ez azt jelenti, ilyenkor hogy csak egy fordulópont van, a
ponttömeg (égitest) a végtelenből jön és a végtelenbe távozik.
Pálya egyenlete:
A mozgásegyenlet radiális komponense:
$$m\left(\ddot{r}-r\dot{\varphi}^2\right)=-G\frac{mM}{r^2}$$
Az impulzusmomentum megmaradását felhasználva
$$\ddot{r}-\frac{N^2}{m^2r^3}=-\frac{GM}{r^2}$$
Ugyanezt kapjuk, ha a radiális mozgást az effektív potenciálban történő
egydimenziós mozgásnak tekintjük.
A pálya egyenlete az $r(\varphi)$ függvény, ezért a $t$ független változóról
áttérünk a $\varphi$ független változóra:
$$\dot{r}=\frac{dr}{dt}=\frac{dr}{d\varphi}\frac{d\varphi}{dt}=\frac{dr}{d\varphi}\dot{\varphi}=\frac{dr}{d\varphi}\frac{N/m}{r^2}$$
amiből
$$\ddot{r}=\frac{d\dot{r}}{dt}=\frac{d^2r}{d\varphi^2}\dot{\varphi}\frac{N/m}{r^2}-\frac{dr}{d\varphi}2\frac{N/m}{r^3}\dot{r}=\frac{d^2r}{d\varphi^2}\frac{(N/m)^2}{r^4}-2\left(\frac{dr}{d\varphi}\right)^2\frac{(N/m)^2}{r^5}$$
Térjünk át a $\xi=1/r$ függő változóra!
$$\frac{dr}{d\varphi}=-\frac{1}{\xi^2}\frac{d\xi}{d\varphi}$$
és
$$\frac{d^2r}{d\varphi^2}=2\frac{1}{\xi^3}\left(\frac{d\xi}{d\varphi}\right)^2-\frac{1}{\xi^2}\frac{d^2\xi}{d\varphi^2}$$
Ezzel
$$\ddot{r}=\frac{N^2}{m^2}\left[2\xi\left(\frac{d\xi}{d\varphi}\right)^2-\xi^2\frac{d^2\xi}{d\varphi^2}-2\xi\left(\frac{d\xi}{d\varphi}\right)^2\right]=-\frac{N^2}{m^2}\xi^2\frac{d^2\xi}{d\varphi^2}$$
A mozgásegyenletből ennek segítségével azt kapjuk, hogy
$$-\xi^2\frac{d^2\xi}{d\varphi^2}-\xi^3=-\frac{Gm^2M}{N^2}\xi^2$$
vagy
$$\frac{d^2\xi}{d\varphi^2}+\xi=\frac{Gm^2M}{N^2}$$
Tovább rendezve:
$$\frac{d^2}{d\varphi^2}\left(\xi-\frac{Gm^2M}{N^2}\right)=-\left(\xi-\frac{Gm^2M}{N^2}\right)$$
Megoldás (v.ö. harmonikus rezgőmozgás egyenlete):
$$\xi-\frac{Gm^2M}{N^2}=K\cos(\varphi-\varphi_0)$$
A $K$ és $\varphi_0$ konstansok integrációs állandók. Ha $K$ pozitív és
$\varphi_0=0$, akkor $\varphi=0$ esetén kapjuk a legnagyobb $\xi$-t, azaz a
Napközelpontot (perihélium). A pálya egyenlete tehát
$$r=\frac{p}{1+\epsilon\cos\varphi}\;,$$
ahol
$$p=\frac{N^2}{Gm^2M}$$
a pálya paramétere és
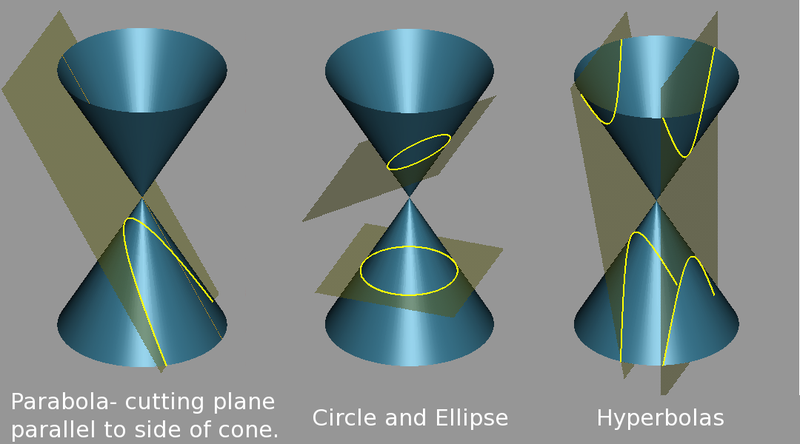
$\epsilon=K\;p$ a pálya excentricitása. Ez kúpszelet egyenlete,
- $\epsilon=0$ esetén kör
- $0<\epsilon<1$ esetén ellipszis (Kepler első törvénye)
- $\epsilon=1$ esetén parabola
- $\epsilon>1$ esetén hiperbola


 bene@arpad.elte.hu
bene@arpad.elte.hu


