


Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
4. hét keddi előadás
Mozgás tömegpont gravitációs terében (folytatás)
Az $1/r$-rel arányos potenciális energiájú centrális centrális erőtérben mozgó
tömegpont pályájának egyenlete
$$r=\frac{p}{1+\epsilon\cos\varphi}\;,$$
ahol
$$p=\frac{N^2}{Gm^2M}$$
a pálya paramétere és
$\epsilon=K\;p$ a pálya excentricitása. Ez kúpszelet egyenlete,
- $\epsilon=0$ esetén kör
- $0<\epsilon<1$ esetén ellipszis (Kepler első törvénye)
- $\epsilon=1$ esetén parabola
- $\epsilon>1$ esetén hiperbola
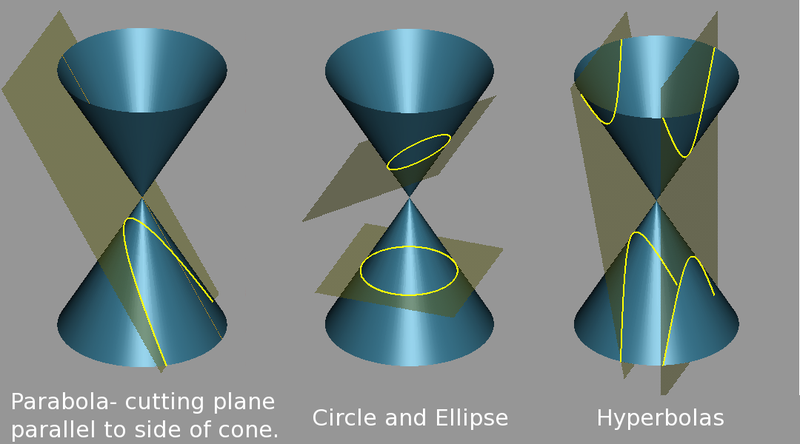
Miért kúpszelet a pálya? Alternatív levezetés:
$$v_\varphi=\frac{N}{mr}$$
és
$$E=\frac{m}{2}v^2-\frac{GmM}{r}$$
az impulzusmomentum és az energia megmaradása alapján. Legyen a pálya
érintőjének a helyvektorral bezárt szöge $\psi$. Ekkor
$$\frac{v_\varphi^2}{v^2}=\sin^2\psi=\frac{\frac{N^2}{m^2}\frac{1}{r^2}}{\frac{2E}{m}+\frac{2GM}{r}}$$
Másrészt a pálya $r(\varphi)$ egyenletével kifejezve
$${\rm ctg}\psi=\frac{1}{r}\frac{dr}{d\varphi}\;,$$
kúpszelet esetén ebből
$${\rm ctg}\psi=\frac{\epsilon\sin\varphi}{1+\epsilon\cos\varphi}$$
ill.
$$\sin^2\psi=\frac{1}{1+{\rm
ctg}^2\psi}=\frac{(1+\epsilon\cos\varphi)^2}{\epsilon^2-1+2(1+\epsilon\cos\varphi)}=\frac{\frac{p^2}{r^2}}{\epsilon^2-1+\frac{2p}{r}}$$
$\sin^2\psi$ két kifejezését összevetve látható, hogy az $r$-függés
ugyanolyan, a pálya tehát kúpszelet. Az együtthatók arányából $p$ és
$\epsilon$ kifejezhetők az energiával és az impulzusmomentummal:
$\begin{eqnarray}
p&=&\frac{N^2}{Gm^2M}\\
\epsilon&=&\sqrt{1+\frac{2E}{m}\left(\frac{N}{GmM}\right)^2}
\end{eqnarray}$
Ellipszispálya esetén a fordulópontok
$$r_{1,2}=\frac{p}{1\pm \epsilon}$$
Ebből
$$\epsilon=p\frac{\xi_1-\xi_2}{2}=\sqrt{1+2mE\left(\frac{N}{Gm^2M}\right)^2}$$
(az összefüggés parabola és hiperbolapályára is érvényes)
Az ellipszis adatai:
- nagytengely:
$$a=\frac{r_1+r_2}{2}=\frac{p}{1- \epsilon^2}=\frac{GmM}{2|E|}$$
- fókuszpont:
$$f=a-r_1=\frac{r_2-r_1}{2}=\frac{p\epsilon}{1- \epsilon^2}=a\epsilon$$
- kistengely:
$$b=\sqrt{a^2-f^2}=\frac{p}{\sqrt{1- \epsilon^2}}=\frac{N}{\sqrt{2m|E|}}$$
Keringési idő:
$$T=\frac{\pi a b}{N/(2m)}=\pi
a\sqrt{\frac{2m}{|E|}}=\frac{2\pi a^{3/2}}{\sqrt{GM}}\;,$$
mivel $\pi a b$ az ellipszis területe és $N/(2m)$ az állandó területi
sebesség.
Másképpen: a keringési idők négyzetei úgy aránylanak egymáshoz, mint a Naptól
mért középtávolságok köbei. (Kepler harmadik törvénye)
A pálya paramétere:
$$p=\frac{2}{\xi_1+\xi_2}=\frac{N^2}{Gm^2M}$$
A pálya excentricitása:
$$\epsilon=\frac{\xi_1-\xi_2}{\xi_1+\xi_2}=\sqrt{1+2mE\left(\frac{N}{Gm^2M}\right)^2}$$
Ellipszispálya esetén ($E<0$)
nagytengely:
Levezetés a centrális erőterek általános formuláiból:
$\begin{eqnarray}\varphi&=&\varphi_0+\int_{r_1}^{r}\frac{\frac{N}{mr^2}dr}{\sqrt{\frac{2}{m}\left(E-V_{eff}\right)}}=\varphi_0+\int_{r_1}^{r}\frac{\frac{N}{mr^2}dr}{\sqrt{\frac{2}{m}\left(E+G\frac{mM}{r}-\frac{N^2}{2mr^2}\right)}}=\varphi_0+\int_{r_1}^{r}\frac{\frac{N}{mr^2}dr}{\sqrt{\frac{2E}{m}+\frac{2GM}{r}-\frac{N^2}{m^2r^2}}}\\
&=&\varphi_0+\int_{r_1}^{r}\frac{\frac{1}{r^2}dr}{\sqrt{\frac{2mE}{N^2}+\frac{2Gm^2M}{N^2}\frac{1}{r}-\frac{1}{r^2}}}
=\varphi_0+\int_{\xi_1}^{\xi}\frac{-d\xi}{\sqrt{\frac{2mE}{N^2}+\frac{2Gm^2M}{N^2}\xi-\xi^2}}=\varphi_0-\int_{\xi_1}^{\xi}\frac{d\xi}{\sqrt{(\xi_1-\xi)(\xi-\xi_2)}}
\end{eqnarray}$
Az integrál kiszámítása:
A gyök alatti kifejezésben az első- és másodfokú tagokat teljes négyzetté
alakítjuk:
$\begin{eqnarray}(\xi_1-\xi)(\xi-\xi_2)&=&-\xi^2+(\xi_1+\xi_2)\xi-\xi_1\xi_2=-\left(\xi-\frac{\xi_1+\xi_2}{2}\right)^2+\left(\frac{\xi_1+\xi_2}{2}\right)^2-\xi_1\xi_2\\&=&\left(\frac{\xi_1-\xi_2}{2}\right)^2-\left(\xi-\frac{\xi_1+\xi_2}{2}\right)^2=\left(\frac{\xi_1-\xi_2}{2}\right)^2\left[1-\left(\frac{\xi-(\xi_1+\xi_2)/2}{(\xi_1-\xi_2)/2}\right)^2\right]
\end{eqnarray}$
Új változó:
$$u=\frac{\xi-(\xi_1+\xi_2)/2}{(\xi_1-\xi_2)/2}$$
Ezzel
$$\int_{\xi_1}^{\xi}\frac{d\xi}{\sqrt{(\xi_1-\xi)(\xi-\xi_2)}}=\int_1^u\frac{du
\;(\xi_1-\xi_2)/2}{(\xi_1-\xi_2)/2\sqrt{1-u^2}}=\int_1^u\frac{du}{\sqrt{1-u^2}}=-\arccos
u=-\arccos{\left(\frac{\xi-(\xi_1+\xi_2)/2}{(\xi_1-\xi_2)/2}\right)}$$
Tehát
$$\varphi=\varphi_0+\arccos{\left(\frac{1/r-(\xi_1+\xi_2)/2}{(\xi_1-\xi_2)/2}\right)}$$
Ha $E<0$ és ennek megfelelően két fordulópont van, az egyik fordulóponttól
a másik fordulópontig éppen $\pi$ a szög változása, tehát a pálya
zárt görbe. Ez az $1/r$-es potenciál sajátossága. Ugyanez a helyzet
$r^2$-es potenciálnál (térbeli harmonikus oszcillátor). Egyéb
esetekben a pálya általában nem záródik.
Ha eltérés van az $1/r$-es potenciáltól (v.ö. általános relativitáselmélet,
$1/r^3$ korrekció), akkor perihélium-elfordulás történik.
Legyen $\varphi_0=0$ (napközelben ekkora a szög). Ekkor
$$\frac{1/r-(\xi_1+\xi_2)/2}{(\xi_1-\xi_2)/2}=\cos\varphi$$
és
$$r=\frac{1}{(\xi_1+\xi_2)/2+((\xi_1-\xi_2)/2)\cos\varphi}=\frac{2/(\xi_1+\xi_2)}{1+\frac{\xi_1-\xi_2}{\xi_1+\xi_2}\cos\varphi}=\frac{p}{1+\epsilon\cos\varphi}$$
Ez kúpszelet (kör, ellipszis, parabola vagy hiperbola) egyenlete.
A pálya paramétere:
$$p=\frac{2}{\xi_1+\xi_2}=\frac{N^2}{Gm^2M}$$
A pálya excentricitása:
$$\epsilon=\frac{\xi_1-\xi_2}{\xi_1+\xi_2}=\sqrt{1+2mE\left(\frac{N}{Gm^2M}\right)^2}$$
Ellipszispálya esetén ($E<0$)
nagytengely:
$$a=\frac{1}{2}\left(r_1+r_2\right)=\frac{r_1r_2}{2}\left(\frac{1}{r_1}+\frac{1}{r_2}\right)=\frac{\xi_1+\xi_2}{2\xi_1\xi_2}=\frac{GmM}{2|E|}$$
kistengely:
$$b=\sqrt{r_1r_2}=\frac{N}{\sqrt{2m|E|}}$$
Keringési idő:
$$T=\frac{\pi a b}{N/(2m)}=\pi
a\sqrt{\frac{2m}{|E|}}=\frac{2\pi a^{3/2}}{\sqrt{GM}}$$
Mivel $\pi a b$ a pálya által körbefogott terület és $N/(2m)$ a területi sebesség.


 bene@arpad.elte.hu
bene@arpad.elte.hu
