Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
4. hét pénteki előadás
A koordináták időfüggése
A radiális koordináta időfüggése ellipszispálya
esetére:
$\begin{eqnarray}
t&=& t_0+\int_{r_1}^{r}\frac{dr}{\sqrt{\frac{2}{m}\left(E-V_{eff}\right)}}
=t_0+\int_{r_1}^{r}\frac{dr}{\sqrt{\frac{2}{m}\left(E+G\frac{mM}{r}-\frac{N^2}{2m r^2}\right)}}=t_0+\int_{r_1}^{r}\frac{r\;dr}{\sqrt{\frac{2E}{m}r^2+2GMr-\frac{N^2}{m^2 }}}\\
&=& t_0+\sqrt{\frac{m}{2|E|}}\int_{r_1}^{r}\frac{\left(\left(r-\frac{r_1+r_2}{2}\right)+\frac{r_1+r_2}{2}\right)\;dr}{\sqrt{(r-r_1)(r_2-r)}}=t_0+\sqrt{\frac{m}{2|E|}}\left\{-\sqrt{(r-r_1)(r_2-r)}+\frac{r_1+r_2}{2}\left[\pi-\arccos{\left(\frac{r-(r_1+r_2)/2}{(r_2-r_1)/2}\right)}\right]\right\}
\end{eqnarray}$
Legyen $$\chi=\pi-\arccos{\left(\frac{r-(r_1+r_2)/2}{(r_2-r_1)/2}\right)}\;,$$
ezzel a változóval az időfüggés paraméteres formában adható meg, ami
tetszőleges számú periódusra érvényes:
$\begin{eqnarray}
r&=&\frac{r_1+r_2}{2}-\frac{r_2-r_1}{2}\cos\chi\\
t&=&t_0+\sqrt{\frac{m}{2|E|}}\left\{\frac{r_1+r_2}{2}\chi-\frac{r_2-r_1}{2}\sin\chi\right\}
\end{eqnarray}$
A pálya adataival kifejezve:
$\begin{eqnarray}
r&=&a\left(1-\epsilon\cos\chi\right)\\
t&=&t_0+\frac{a^{3/2}}{\sqrt{GM}}\left(\chi-\epsilon\sin\chi\right)
\end{eqnarray}$
Az azimutszögre:
$$\cos\varphi=\frac{\cos\chi-\epsilon}{1-\epsilon\cos\chi}$$
Parabolapálya esetén ($E=0$):
$$t=t_0+\int_{r_1}^{r}\frac{dr}{\sqrt{\frac{2GM}{r}-\frac{N^2}{m^2r^2}}}=
t_0+\frac{1}{\sqrt{2GM}}\int_{r_1}^{r}\frac{\left(\left(r-r_1\right)+r_1\right)\;dr}{\sqrt{(r-r_1)}}=t_0+\frac{1}{\sqrt{2GM}}\left(\frac{2}{3}(r-r_1)^{3/2}+2(r-r_1)^{1/2}\right)$$
Hiperbolapálya esetén ($E>0$):
$$t=t_0+\int_{r_1}^{r}\frac{dr}{\sqrt{\frac{2}{m}\left(E-V_{eff}\right)}}=
t_0+\sqrt{\frac{m}{2E}}\int_{r_1}^{r}\frac{\left(\left(r-\frac{r_1+r_2}{2}\right)+\frac{r_1+r_2}{2}\right)\;dr}{\sqrt{(r-r_1)(r-r_2)}}=t_0+\sqrt{\frac{m}{2E}}\left\{\sqrt{(r-r_1)(r-r_2)}+\frac{r_1+r_2}{2}{\rm
ar
ch}\left(\frac{r-(r_1+r_2)/2}{(r_1-r_2)/2}\right)\right\}$$
Paraméteres alakban:
legyen
$$\chi={\rm arch}\left(\frac{r-(r_1+r_2)/2}{(r_1-r_2)/2}\right)$$
ekkor
$\begin{eqnarray}
r&=&\frac{r_1+r_2}{2}-\frac{r_1-r_2}{2}\cosh\chi\\
t&=&t_0+\sqrt{\frac{m}{2E}}\left\{\frac{r_1+r_2}{2}\chi+\frac{r_1-r_2}{2}\sinh\chi\right\}
\end{eqnarray}$
Mesterséges égitestek mozgása
Körsebesség (első kozmikus sebesség)
Körpálya:
mozgásegyenlet radiális komponense:
$$m\frac{v^2}{r}=G\frac{mM}{r^2}$$
Ebből
$$v=\sqrt{\frac{GM}{r}}=\sqrt{g\;r}\;,$$
mivel ha $r$ a Föld sugara, akkor $(GM)/r^2=g$ a nehézségi gyorsulás.
A korábbi általános formulákból:
$$\epsilon=0\;\Rightarrow\;E=-\frac{G^2m^3M^2}{2N^2}$$
és
$$r=p=\frac{GmM}{2|E|}=\frac{N^2}{Gm^2M}$$
Ez az energiaérték egyben - adott nagyságú impulzusmomentum ($N$) esetén - az effektív potenciál minimumértéke is:
$$0=\frac{dV_{eff}}{dr}=\frac{d}{dr}\left(-G\frac{mM}{r}+\frac{N^2}{2mr^2}\right)= G\frac{mM}{r^2}-\frac{N^2}{mr^3}$$
A minimumhely tehát
$$r_{min}=\frac{N^2}{Gm^2M}\;$$
a minimum értéke pedig
$$V_{eff, min}=-G\frac{mM}{r_{min}}+\frac{N^2}{2mr_{min}^2}=-\frac{Gm^3M^2}{2N^2}$$
Az általános összefüggések alapján (ld. egydimenziós mozgás tulajdonságai)
következik, hogy ez az adott impulzusmomentum mellett lehetséges legkisebb mechanikai energia, továbbá $E=V_{eff, min}$ esetén $r=\text{állandó}=r_{min}$.
Ha a körpálya sugarát ismerjük, abból az impulzusmomentum
$$N=\sqrt{Gm^2Mr}$$
Másfelől $N=mrv$, így a körsebességre
$$v=\sqrt{\frac{GM}{r}}\approx 7.9 \;\frac{km}{s}$$
Gravitációs állandó: $$G=6,67 \times 10^{-11}\;\frac{m^3}{kg \;s^2}$$
Föld tömege:
$$M=5,97\times 10^{24}\;kg$$
Föld sugara:
$$r=6378\; km$$
Szökési sebesség (második kozmikus sebesség)
A Föld felszínéről a végtelenbe távozáshoz szükséges minimális sebesség:
Sugárirányú mozgás esetén a Föld felszínén és a végtelenben egyaránt felírjuk a mechanikai energiát. Az utóbbi minimális értéke nulla, ezért az energiamegmaradásból:
$$\frac{m}{2}v^2-G\frac{mM}{r}=0$$
Innen a szökési sebesség:
$$v=\sqrt{\frac{2GM}{r}}=\sqrt{2gr}\approx 11\; \frac{km}{s}$$
Ez a körsebesség $\sqrt{2}$-szöröse.
A korábbi általános formulákból:
Végtelenbe távozáshoz legalábbis parabolapálya kell:
$$\epsilon=1\;\Rightarrow\;E=0$$
A pálya $p$ paramétere az impulzusmomentumtól függ, de bármi is az értéke, az energiamegmaradásból ugyanazt kapjuk a szökési sebességre, mint tisztán sugárirányú mozgás esetén. A fordulópontot az effektív potenciál zérushelye,
$$r_0=\frac{N^2}{2Gm^2M}$$
szolgáltatja. A Föld felszínéről induló rakéta esetén nyilván $r\ge r_0$, amiből
$$N\le m\sqrt{2GMr}$$
A legnagyobb impulzusmomentumot akkor kapjuk, ha itt az egyenlőség teljesül. Ekkor a sebesség vízszintes irányú és $N=mrv$. Az előbbi egyenlőségbe ezt behelyettesítve természetesen ilyenkor is a szökési sebesség $v=\sqrt{(2GM)/r}$ formulája adódik.
Mozgás taszító Coulomb-potenciálban: Rutherford-szórás
Rutherford-kísérlet: nagy energiájú ($4.8\; MeV$) $\alpha$-részecskék szóródnak aranyfólián.
(Geiger-Marschden-kísérlet vagy Rutherford-kísérlet, 1909-1911)
Arany rendszáma: $79$, tömegszáma: $199$, atomsugara: $2\times 10^{-10}\;m$.
$\alpha$-rész rendszáma: $2$, tömegszáma: $4$.
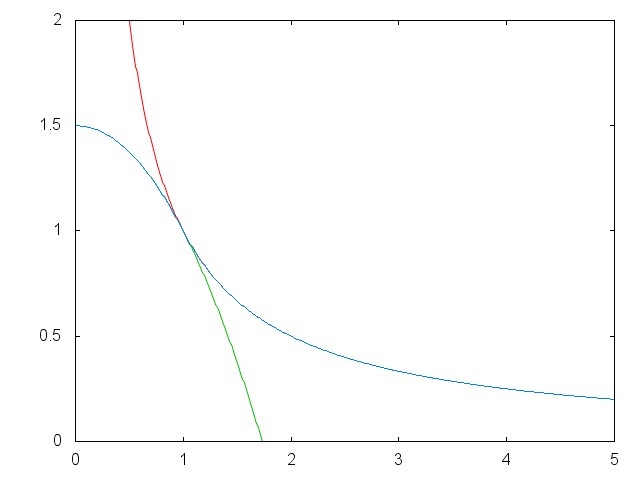A potenciális energia az atommag közelében
$\begin{eqnarray}
V(r)=\left\{
\begin{array}{lcl}
-\int_{\infty}^r \frac{1}{4\pi \epsilon_0}\frac{Z_1Z_2 q_e^2}{r^2}dr =
\frac{1}{4\pi \epsilon_0}\frac{Z_1Z_2 q_e^2}{r}
&
{\rm ha} & r > R\\
-\int_{\infty}^R \frac{1}{4\pi \epsilon_0}\frac{Z_1Z_2 q_e^2}{r^2}dr-
\int_{R}^r \frac{1}{4\pi \epsilon_0}\frac{Z_1Z_2
q_e^2}{r^2}\frac{r^3}{R^3}dr = \frac{3}{2}\frac{1}{4\pi \epsilon_0}\frac{Z_1Z_2 q_e^2}{R}\left(1-\frac{r^2}{3R^2}\right) & {\rm ha} & r < R
\end{array}\right.
\end{eqnarray}$
Itt $R$ az atommag sugara.
Mivel a bombázó részecske visszaverődik az atommagon,
$$ \frac{3}{2}\frac{1}{4\pi \epsilon_0}\frac{Z_1Z_2 q_e^2}{R}>E$$
amiből
$$R<7\times 10^{-14}\; m$$
Ténylegesen $R\approx 7\times 10^{-15}\; m$.
A tömegvonzás törvénye
Nehézségi gyorsulás a Föld felszínén
bene@arpad.elte.hu