Elméleti fizika I.

Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
3. hét csütörtöki előadás

Csillapított harmonikus rezgőmozgás
$$m\ddot{x}=-Dx-k\dot{x}$$ vagy $$\ddot{x}+2\alpha\dot{x}+\omega_0^2x=0$$ Itt $\alpha=\frac{k}{2m}$ és $\omega_0=\sqrt{\frac{D}{m}}$. Keressük a megoldást exponenciális alakban, azaz tegyük fel, hogy $$x=A{\rm e}^{\kappa t}$$ Azt kapjuk, hogy $$\kappa^2+2\alpha\kappa+\omega_0^2=0$$ Tehát $$\kappa=-\alpha\pm\sqrt{\alpha^2-\omega_0^2}$$

$\quad\alpha>\omega_0\quad$: két valós, negatív gyök. Általános megoldás: $$x(t)=A_1{\rm e}^{\kappa_1 t}+A_2{\rm e}^{\kappa_2 t}\equiv A_1{\rm e}^{-|\kappa_1 |t}+A_2{\rm e}^{-|\kappa_2| t} $$ Túlcsillapított rezgések (pl. lengéscsillapító).
$\quad\alpha<\omega_0\quad$: két negatív valós részű, konjugált komplex gyök.
Mit jelent ez? Mivel $${\rm e}^{ix}=\cos(x)+i\sin(x)\;,$$ ilyenkor $$x(t)={\rm e}^{-\alpha t}\left(a\cos(\Omega t)+b\sin(\Omega t)\right)\equiv A{\rm e}^{-\alpha t}\cos(\Omega t+\delta) $$ a megoldás. Itt $$\Omega=\sqrt{\omega_0^2-\alpha^2}$$ Csillapított harmonikus rezgések.
$\quad\alpha=\omega_0\quad$: két egyenlő, negatív gyök. Megoldás: $$x(t)=\lim_{\Omega\rightarrow 0}{\rm e}^{-\alpha t}\left(a\cos(\Omega t)+b\frac{\sin(\Omega t)}{\Omega}\right)={\rm e}^{-\alpha t}\left(a+bt\right)$$

Kényszerrezgések, rezonancia
Mi történik, ha egy csillapított harmonikus oszcillátort periodikusan gerjesztünk? $$m\ddot{x}=-Dx-k\dot{x}+F\cos(\omega t)$$ avagy $$\ddot{x}+2\alpha\dot{x}+\omega_0^2 x=f\cos(\omega t)$$ Itt $f=F/m$.
Komplex írásmód (a valós résznek van fizikai tartalma, de az egyenlet linearitása miatt elég a számolás végén meghatározni a valós részt): $$\ddot{x}+2\alpha\dot{x}+\omega_0^2 x=f{\rm e}^{i\omega t}$$ Egy partikuláris megoldás: $$x=A{\rm e}^{i\omega t}$$ ahol $A$ ezúttal határozott értékű lesz, mivel $$A\left(-\omega^2+2i\alpha\omega+\omega_0^2 \right)=f$$ Ebből $$A=\frac{f}{\omega_0^2-\omega^2+2i\alpha\omega}=\frac{f}{\sqrt{\left(\omega_0^2-\omega^2\right)^2+4\alpha^2\omega^2}}{\rm e}^{-i\delta}$$ ahol $$\delta={\rm arctg}\left(\frac{2\alpha\omega}{\omega_0^2-\omega^2}\right)$$ Tehát $$x=\frac{f}{\sqrt{\left(\omega_0^2-\omega^2\right)^2+4\alpha^2\omega^2}} \cos(\omega t-\delta)$$ Kényszerrezgés.
Ehhez még a homogén egyenlet, $$\ddot{x}+2\alpha\dot{x}+\omega_0^2 x=0$$ tetszőleges megoldása hozzáadható (tranziensek): $$x=\frac{f}{\sqrt{\left(\omega_0^2-\omega^2\right)^2+4\alpha^2\omega^2}} \cos(\omega t-\delta)+{\rm e}^{-\alpha t}\left(a\cos(\Omega t)+b\sin(\Omega t)\right)$$ Megjegyzés: A tranziensek lehetnek túlcsillapított rezgések is.

Az impulzus megmaradása
Impulzus (mozgásmennyiség): $${\bf p}=m{\bf v}$$ A dinamika alaptörvénye az impulzussal kifejezve: $${\bf F}=\frac{d{\bf p}}{dt}$$ Vagy másképpen: $$\Delta{\bf p}=\int {\bf F}dt$$ Két test kölcsönhatásakor a hatás-ellenhatás törvénye értelmében $${\bf F}_{12}=-{\bf F}_{21}\quad\Rightarrow\quad \frac{d}{dt}\left({\bf p}_1+{\bf p}_2\right)=0$$ Megjegyzés: Az impulzus megmaradása a térbeli eltolási szimmetria következménye. Ha pl. a potenciál nem függ az $x$ koordinátától, akkor $$F_x=-\frac{\partial V}{\partial x}=0\quad\Rightarrow\quad \dot{p_x}=0$$

A mozgás ábrázolása fázistérben

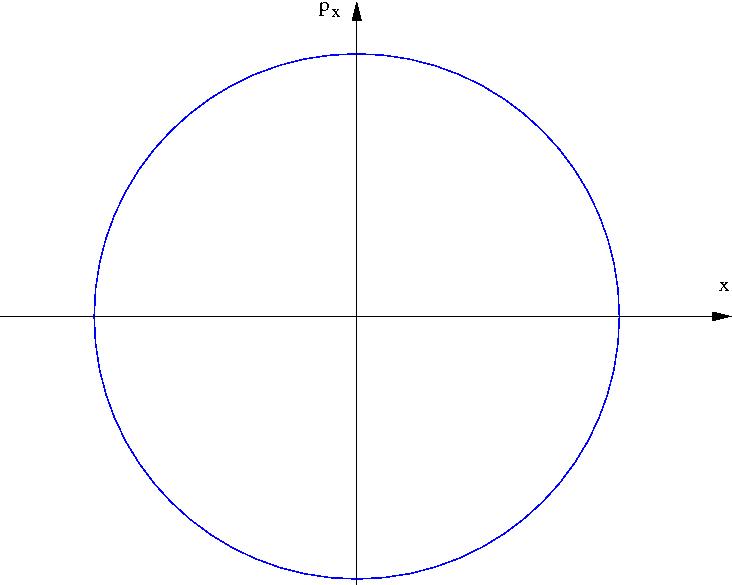
Harmonikus oszcillátor fázistrajektóriája (ellipszis) $$E=\frac{m}{2}v_x^2+\frac{1}{2}m\omega^2x^2=\frac{p_x^2}{2m}+\frac{1}{2}m\omega^2x^2$$ $$\frac{p_x^2}{2mE}+\frac{x^2}{2E/(m \omega^2)}=1$$ Az ellipszis tengelyei $\sqrt{2mE}$ ill. $\sqrt{\frac{2E}{m \omega^2}}$ hosszúságúak.

A mozgásegyenletek numerikus megoldása
$$\ddot{x}=f(x,\dot{x})$$ Átalakítás elsőrendű egyenletrendszerré: $\begin{eqnarray} \dot{x}&=&v\\ \dot{v}&=&f(x,v,t) \end{eqnarray}$ Explicit Euler-módszer: $\begin{eqnarray} t^{(n+1)}&=&t^{(n)}+dt\\ x^{(n+1)}&=&x^{(n)}+v^{(n)}dt\\ v^{(n+1)}&=&v^{(n)}+f(x^{(n)},v^{(n)},t^{(n)})dt \end{eqnarray}$ A hiba $dt^2$ nagyságrendű.

Középpont-módszer (másodrendű Runge-Kutta): $\begin{eqnarray} t^{(n+1/2)}&=&t^{(n)}+dt/2\\ x^{(n+1/2)}&=&x^{(n)}+v^{(n)}dt/2\\ v^{(n+1/2)}&=&v^{(n)}+f(x^{(n)},v^{(n)},t^{(n)})dt/2\\ t^{(n+1)}&=&t^{(n)}+dt\\ x^{(n+1)}&=&x^{(n)}+v^{(n+1/2)}dt\\ v^{(n+1)}&=&v^{(n)}+f(x^{(n+1/2)},v^{(n+1/2)},t^{(n+1/2)})dt \end{eqnarray}$ A hiba $dt^3$ nagyságrendű.

bene@arpad.elte.hu