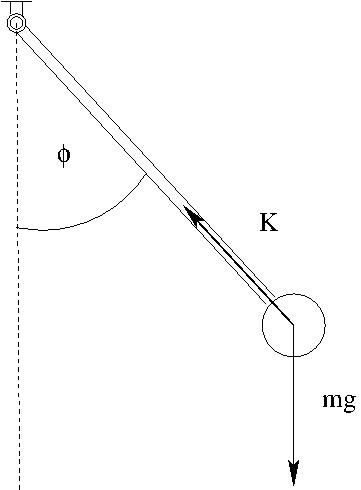Mozgásegyenletek:

• radiális komponens: $$m l \dot{\phi}^2 =K-mg\cos\phi$$
• tangenciális komponens: $$m l\ddot{\phi}=-mg\sin\phi$$

A potenciális energia a kitérés szögének függvényében. A két vízszintes vonal a mechanikai energia két különböző értékének felel meg. A zöld vonalnak megfelelő energia esetén lengés, a kék vonalnak megfelelő energia esetén forgás valósul meg.

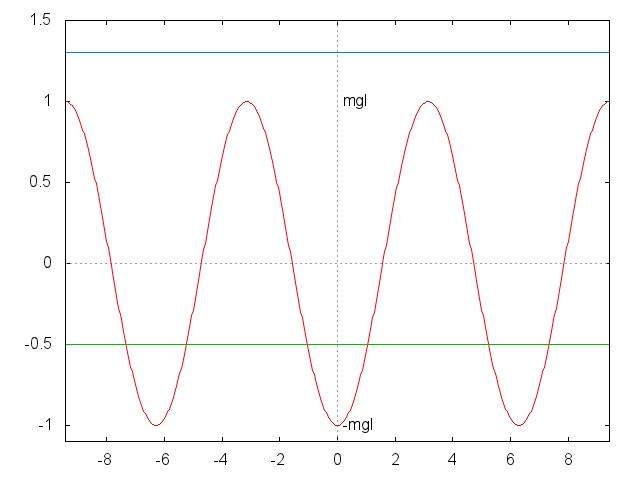• Ha $-mgl\le E\le mgl$, a mozgás lengés két holtpont, $\pm \phi_0$ között, ahol $$\cos\phi_0=-\frac{E}{mgl}\;.$$ A holtpontokban $\dot{\phi}$ előjelet vált, azaz $\dot{\phi}(\phi_0)=0$.
• Ha $E>mgl$, akkor a mozgás forgás, $\dot{\phi}$ előjele változatlan és a szögsebesség nem válik nullává.

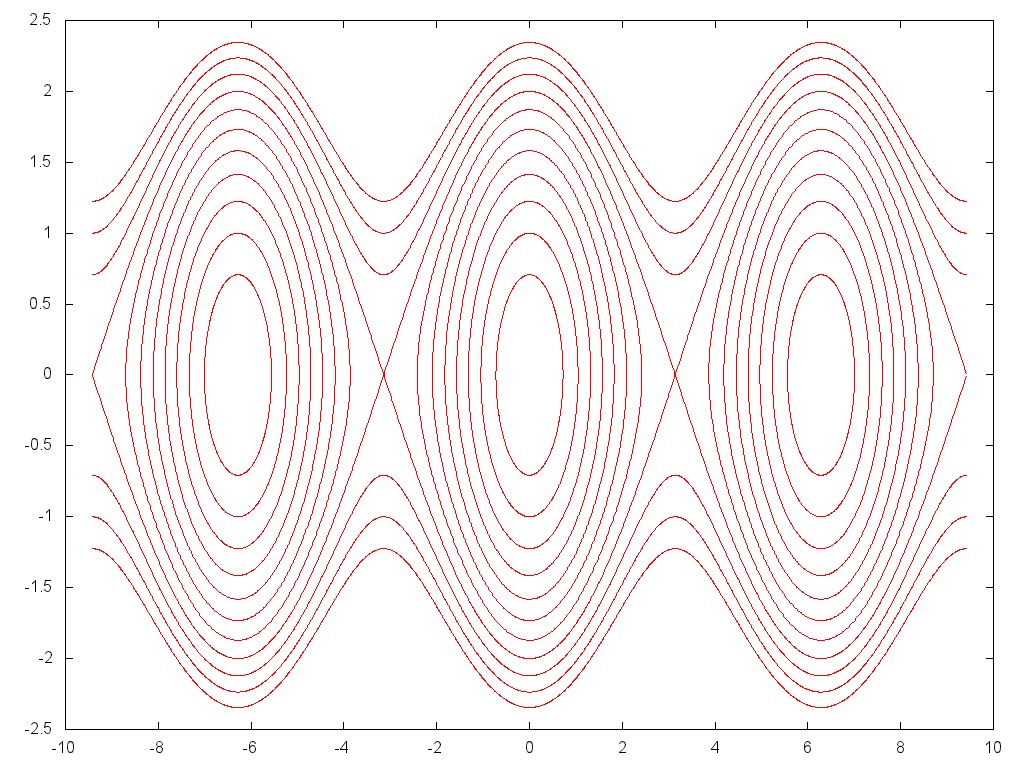
A $\dot{\phi}$ szögsebesség a kitérés $\phi$ szögének függvényében különféle energiákon. A lengést és forgást elválasztó szeparátrix az $E=mgl$ energiához tartozik.

• Ha $E>mgl$, $$t=t_0+\sqrt{\frac{mgl^2}{2g(E+mgl)}}\int_0^\phi \frac{d\phi'}{\sqrt{1-\frac{2mgl}{E+mgl}\sin^2\left( \frac{\phi'}{2}\right)}}=t_0+kF\left(\frac{\phi}{2},k\right)\sqrt{\frac{l}{g}}$$ Itt $F(x,k)$ az elsőfajú nem teljes elliptikus integrál. A paraméter értéke $$k=\sqrt{\frac{2mgl}{E+mgl}}\;.$$ Invertálva: $$\sin\left(\frac{\phi}{2}\right)={\rm sn}\left(\frac{1}{k}\sqrt{\frac{g}{l}}(t-t_0),k\right)\;,$$ ahol az ${\rm sn}(x,k)$ Jacobi-féle elliptikus függvény az elsőfajú nem teljes elliptikus integrál inverzének szinusza.
  Periódusidő: $$T=4kK(k)\sqrt{\frac{l}{g}}$$ Itt $K(k)=F(\pi/2,k)$ az elsőfajú teljes elliptikus integrál.
• Ha $-mgl\le E\le mgl$, legyen $$k=\sqrt{\frac{E+mgl}{2mgl}}$$ és $$\sin\zeta=\sqrt{\frac{2mgl}{E+mgl}}\sin\left( \frac{\phi'}{2}\right)\;.$$ Ekkor $$t=t_0+\sqrt{\frac{l}{g}}\int_0^{\arcsin(\sin(\phi/2)/k))}\frac{d\zeta}{\sqrt{1-k^2\sin^2\zeta}}=F\left(\arcsin\left(\frac{1}{k}\sin\left(\frac{\phi}{2}\right)\right),k\right)\sqrt{\frac{l}{g}}$$ Invertálva: $$\sin\left(\frac{\phi}{2}\right)=k\;{\rm sn}\left(\sqrt{\frac{g}{l}}(t-t_0),k\right)$$ Periódusidő: $$T=4K(k)\sqrt{\frac{l}{g}}$$

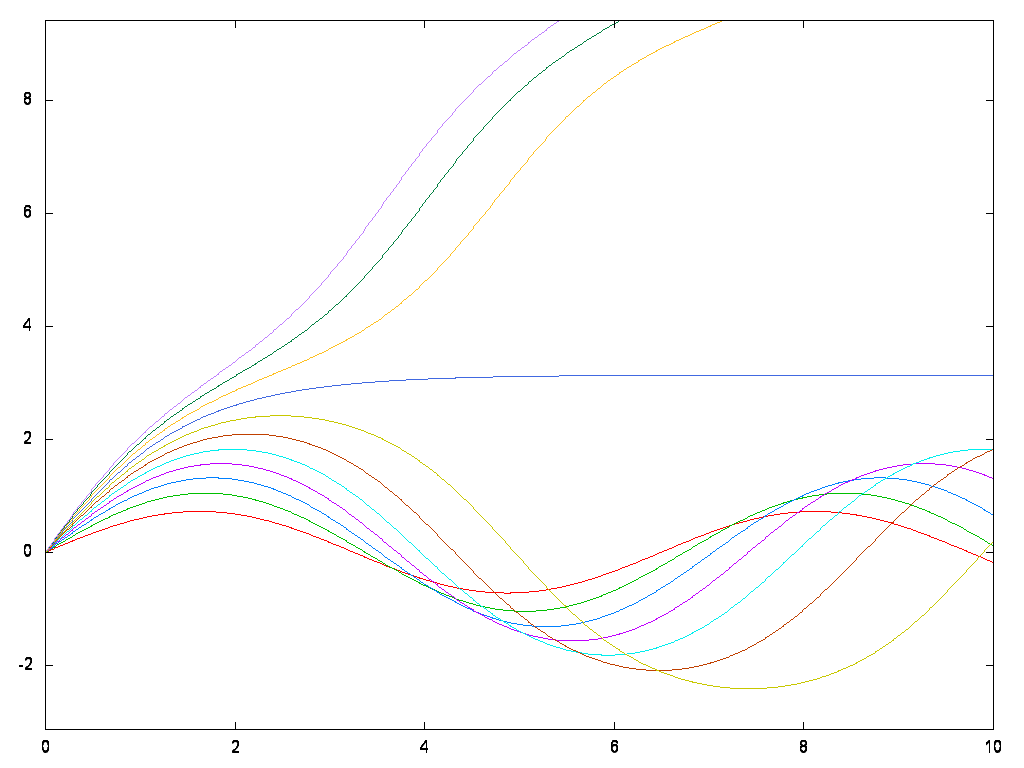
  A szögkitérés az idő függvényében különböző energiákon.

  
  

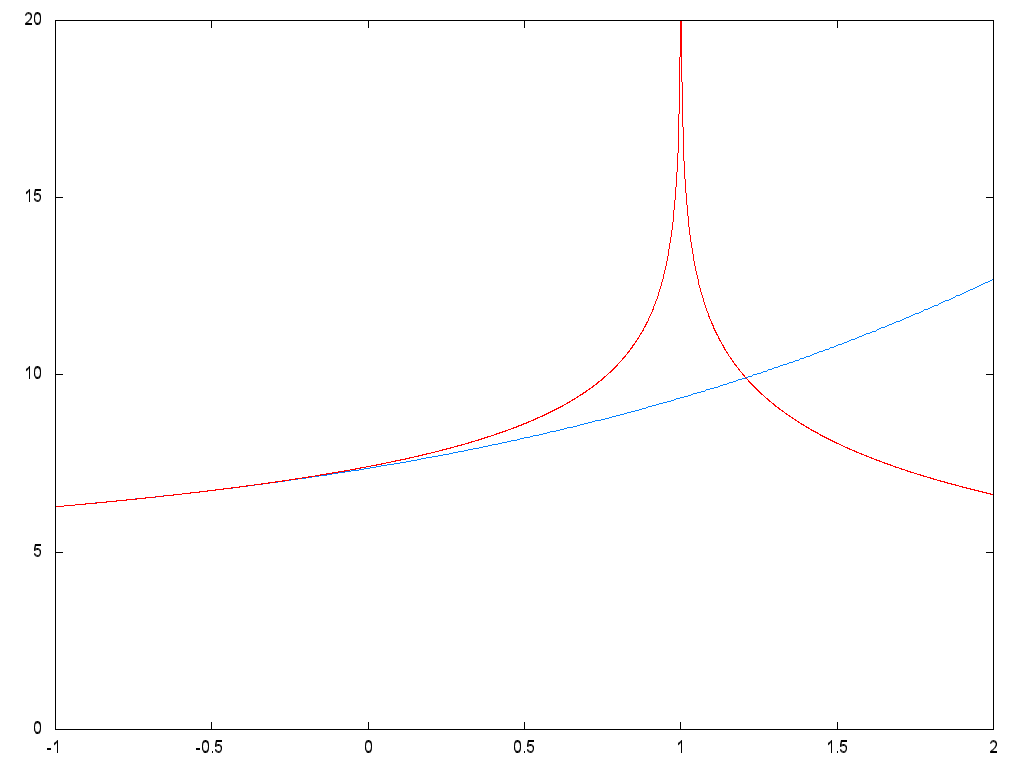
  Piros színű görbe: a periódusidő az energia függvényében. A potenciális energia nullszintje a felfüggesztési pont. Az energia $mgl$ egységekben, a periódusidő $\sqrt{l/g}$ egységekben van feltüntetve. Kék színű görbe: az alábbi, kis kitérésekre érvényes közelítő formula.

  
  A periódusidő kis kitérések esetén: $\begin{eqnarray} T&=&4K(k)\sqrt{\frac{l}{g}}=4\sqrt{\frac{l}{g}}\int_0^{\pi/2}\frac{d\zeta}{\sqrt{1-k^2\sin^2\zeta}}=4\sqrt{\frac{l}{g}}\int_0^{\pi/2}\left(1+\frac{1}{2}k^2\sin^2\zeta+\frac{3}{8}k^4\sin^4\zeta+\frac{5}{16}k^6\sin^6\zeta+\dots\right)d\zeta\\ &=& 2\pi \sqrt{\frac{l}{g}}\left(1+\frac{1}{4}k^2+\frac{9}{64}k^4+\frac{25}{256}k^6+\dots \right)=2\pi \sqrt{\frac{l}{g}}\left( 1+\frac{1}{4}\frac{E+mgl}{2mgl}+\frac{9}{64}\left(\frac{E+mgl}{2mgl} \right)^2+\frac{25}{256}\left(\frac{E+mgl}{2mgl} \right)^3+\dots \right)\\ &=& 2\pi \sqrt{\frac{l}{g}}\left(1+\frac{1}{4}\sin^2\left( \frac{\phi_0}{2} \right)+\frac{9}{64}\sin^4\left(\frac{\phi_0}{2} \right)+\frac{25}{256}\sin^6\left(\frac{\phi_0}{2} \right)+\dots\right)\\ &=& 2\pi \sqrt{\frac{l}{g}} \left( 1+\frac{1}{16}\phi_0^2 +\frac{11}{3072}\phi_0^4 +\frac{173}{737280}\phi_0^6+\dots\right) \end{eqnarray}$