


Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
10. hét pénteki előadás
Merev testek dinamikája II.
Merev test helyzetének megadása Euler-szögekkel
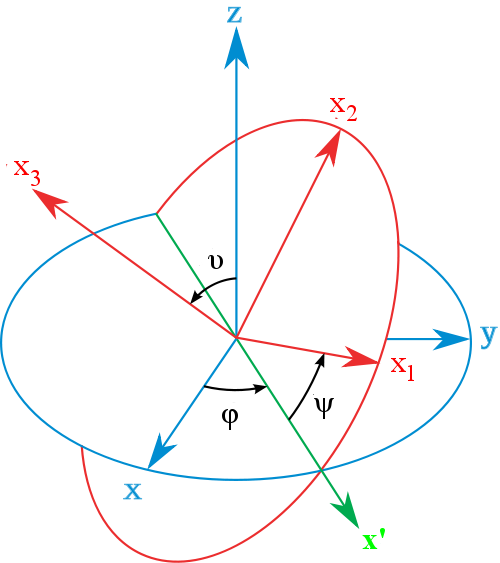
- Az $x$, $y$, $z$ kordinátarendszer inerciarendszer.
- Az $x_1$, $x_2$, $x_3$ tengelyek a fő tehetetlenségi tengelyek, ebben a
kordinátarendszerben tehát a ${\bf {\bf \Theta}}$ tehetetlenségi tenzor
diagonális
$${\bf {\bf \Theta}}=\left(\begin{array}{ccc}{\Theta}_1&0&0\\0&{\Theta}_2&0\\0&0&{\Theta}_3\end{array}\right)$$
A szögsebesség vektora felfogható a következő három vektor összegeként:
- $\dot{\vartheta}$ nagyságú, $x'$ irányú vektor
- $\dot{\varphi}$ nagyságú, $z$ irányú vektor
- $\dot{\psi}$ nagyságú, $x_3$ irányú vektor
Az $\omega$ szögsebességvektor komponenseit akár az $x_1$, $x_2$, $x_3$, akár
az $x$, $y$, $z$ kordinátarendszerben ezen vektorok megfelelő komponenseinek
összeadásával lehet kiszámítani:
- az $x_1$, $x_2$, $x_3$ kordinátarendszerben
$
\begin{eqnarray}
\omega_1&=& \phantom{-}\dot{\vartheta}\cos\psi&+&\dot{\varphi}\sin\vartheta\sin\psi&&\\
\omega_2&=&-\dot{\vartheta}\sin\psi&+&\dot{\varphi}\sin\vartheta\cos\psi&&\\
\omega_3&=&&&\dot{\varphi}\cos\vartheta&&+\dot{\psi}
\end{eqnarray}
$
- az $x$, $y$, $z$ kordinátarendszerben
$
\begin{eqnarray}
\omega_x&=&\dot{\vartheta}\cos\varphi && &+&\dot{\psi}\sin\vartheta\sin\varphi\\
\omega_y&=&\dot{\vartheta}\sin\varphi && &-&\dot{\psi}\sin\vartheta\cos\varphi\\
\omega_z&=& &&\dot{\varphi} &+&\dot{\psi}\cos\vartheta
\end{eqnarray}
$
Szimmetrikus pörgettyű erőmentes mozgása
Mutasson az inerciarendszer $z$ tengelye a megmaradó ${\bf N}$ impulzusmomentum
irányába. Ekkor az impulzusmomentum komponensei az $x_1$, $x_2$, $x_3$ kordinátarendszerben
$
\begin{eqnarray}
N_1&=& N\sin\vartheta\sin\psi\\
N_2&=& N\sin\vartheta\cos\psi\\
N_3&=& N\cos\vartheta
\end{eqnarray}
$
Másrészt $N_1={\Theta}_1\omega_1\;,\quad N_2={\Theta}_2\omega_2\;,\quad
N_3={\Theta}_3\omega_3\;$, ezért
$
\begin{eqnarray}
\frac{N}{{\Theta}_1}\sin\vartheta\sin\psi&=&\phantom{-}\dot{\vartheta}\cos\psi&+&\dot{\varphi}\sin\vartheta\sin\psi&&\\
\frac{N}{{\Theta}_2}\sin\vartheta\cos\psi&=&-\dot{\vartheta}\sin\psi&+&\dot{\varphi}\sin\vartheta\cos\psi&&\\
\frac{N}{{\Theta}_3}\cos\vartheta&=& &&\dot{\varphi}\cos\vartheta&&+\dot{\psi}
\end{eqnarray}
$
Ha ${\Theta}_1={\Theta}_2$, akkor az első két egyenletből
$$\dot{\vartheta}=0$$
és
$$\dot{\varphi}=\frac{N}{{\Theta}_1}$$
következik. A pörgettyű $x_3$ szimmetriatengelye tehát $N/{\Theta}_1$
szögsebességgel precesszál a megmaradó impulzusmomentum-vektor körül úgy, hogy
az azzal bezárt $\vartheta$ szöge a mozgás során állandó.
Aszimmetrikus pörgettyű szabad forgása, főtengelyek stabilitása
Tfh. mindhárom fő tehetetlenségi nyomaték különböző, mégpedig
$${\Theta}_1>{\Theta}_2>{\Theta}_3>0$$
Energiamegmaradás:
$$E=\frac{N_1^2}{2{\Theta}_1}+\frac{N_2^2}{2{\Theta}_2}+\frac{N_3^2}{2{\Theta}_3}$$
vagy
$$\frac{N_1^2}{2E{\Theta}_1}+\frac{N_2^2}{2E{\Theta}_2}+\frac{N_3^2}{2E{\Theta}_3}=1$$
Ez az $N_1$, $N_2$, $N_3$ változókban ellipszoid egyenlete, melynek
fél főtengelyei
$\sqrt{2E{\Theta}_1}>\sqrt{2E{\Theta}_2}>\sqrt{2E{\Theta}_3}>0$ hosszúságúak.
Impulzusmomentum-megmaradás:
$$N^2=N_1^2+N_2^2+N_3^2$$
vagy
$$\frac{N_1^2}{N^2}+\frac{N_2^2}{N^2}+\frac{N_3^2}{N^2}=1$$
Ez $N$ sugarú gömb egyenlete. Mivel mindkét egyenlet egyidejűleg teljesül, az
${\bf N}$ vektor csak az ellipszoid-felület és a gömbfelület metszésvonalán
mozoghat. Ez az észrevétel lehetővé teszi az egyes főtengelyek körüli forgás
stabilitásának vizsgálatát:
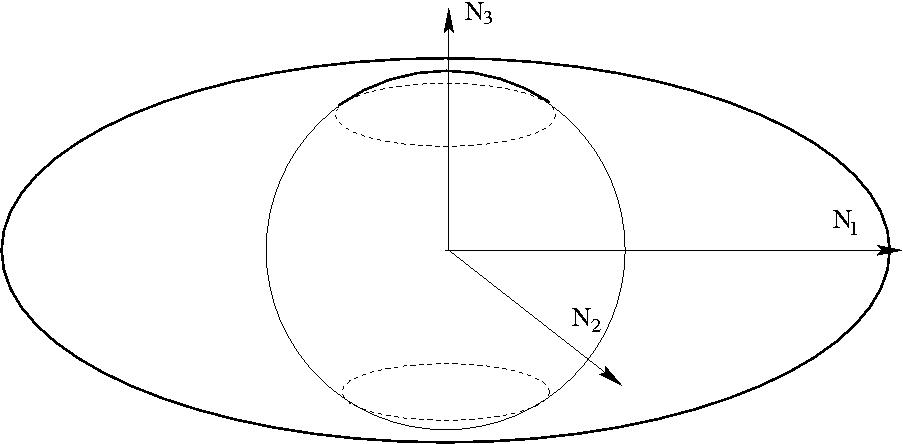
A legkisebb fő tehetetlenségi nyomatékhoz tartozó tengely körüli forgás
stabil.
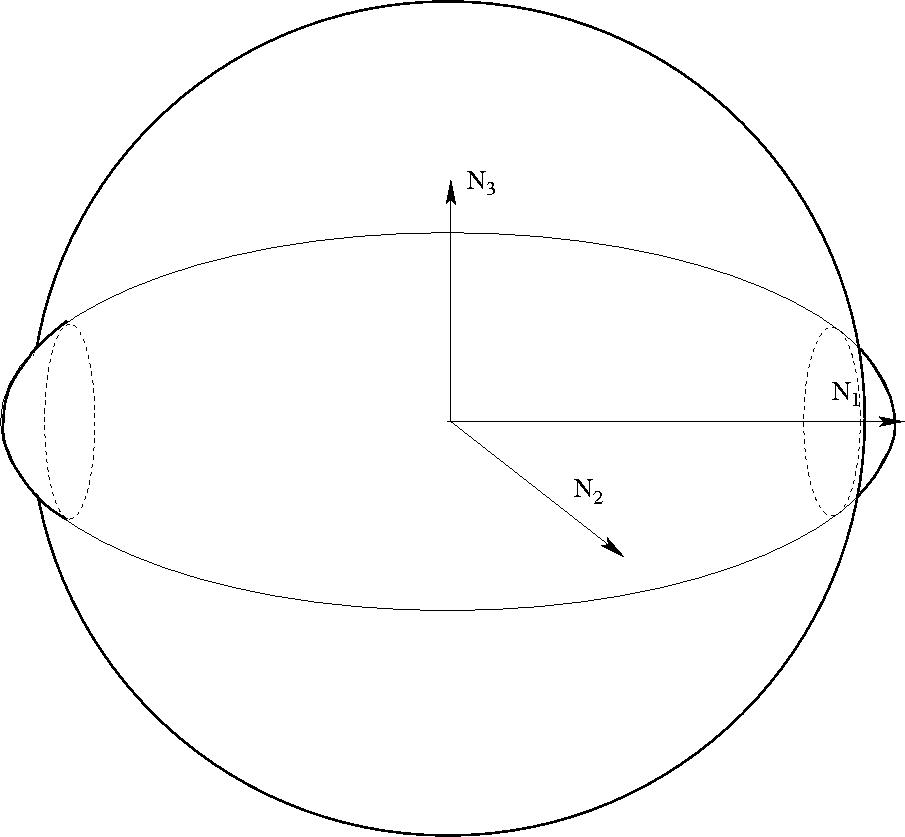
A legnagyobb fő tehetetlenségi nyomatékhoz tartozó tengely körüli forgás
is stabil.
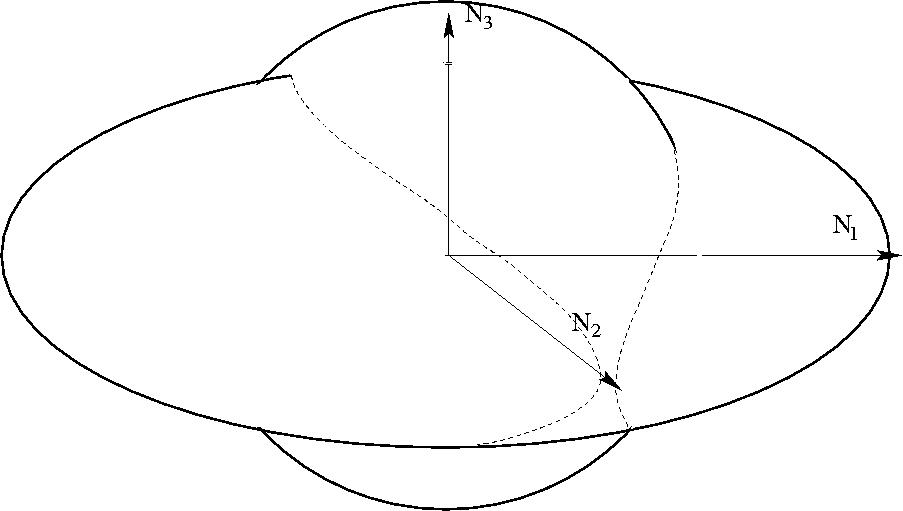
A középső fő tehetetlenségi nyomatékhoz tartozó tengely körüli forgás
instabil.
Vigyázat! Az ábrákon a megmaradási tételeket kifejező geometriai
alakzatok láthatók, nem a ténylegesen forgó test!
A forgás dinamikai egyenlete a főtengelyek által
meghatározott koordináta-rendszerben: Euler-egyenletek
Az inerciarendszerbeli időderivált ($d/dt$)és a merev testtel együtt forgó
rendszerbeli időderivált ($d'/dt$) kapcsolata (vektorra alkalmazandó):
$$\frac{d}{dt}=\frac{d'}{dt}+\vec{\bf \omega}\times$$
Az impulzusmomentum vektorára alkalmazva:
$$\frac{d {\bf N}}{dt}=\frac{d' {\bf N}}{dt}+\vec{\bf \omega}\times {\bf N}$$
Inerciarendszerben
$$\frac{d {\bf N}}{dt}={\bf M}$$
ahol ${\bf M}$ a testre ható impulzusmomentum.
Együttforgó rendszerben tehát
$$\frac{d' {\bf N}}{dt}+\vec{\bf \omega}\times {\bf N}={\bf M}$$
Mivel az $x_1$, $x_2$, $x_3$ kordinátarendszerben
$$N_1={\Theta}_1\omega_1\;,\quad N_2={\Theta}_2\omega_2\;,\quad N_3={\Theta}_3\omega_3\;,$$
a fenti egyenlet komponensei
$\begin{eqnarray}
{\Theta}_1\dot{\omega_1}+\left({\Theta}_3-{\Theta}_2\right)\omega_2\omega_3&=& M_1\\
{\Theta}_2\dot{\omega_2}+\left({\Theta}_1-{\Theta}_3\right)\omega_3\omega_1&=& M_2\\
{\Theta}_3\dot{\omega_3}+\left({\Theta}_2-{\Theta}_1\right)\omega_1\omega_2&=& M_3
\end{eqnarray}$
Euler-egyenletek alkalmazása : szimmetrikus pörgettyű
erőmentes mozgása
$M_1=M_2=M_3=0$, ${\Theta}_1={\Theta}_2\ne {\Theta}_3$ esetén:
$\begin{eqnarray}
{\Theta}_1\dot{\omega_1}+\left({\Theta}_3-{\Theta}_1\right)\omega_2\omega_3&=& 0\\
{\Theta}_1\dot{\omega_2}+\left({\Theta}_1-{\Theta}_3\right)\omega_3\omega_1&=& 0\\
{\Theta}_3\dot{\omega_3}&=& 0
\end{eqnarray}$
Tehát $\omega_3$ állandó. A másik két egyenlet az $\omega_1$, $\omega_2$
változókban körmozgás egyenlete
$$\Omega=\frac{{\Theta}_3-{\Theta}_1}{{\Theta}_1} \omega_3$$
szögsebességgel, azaz
$$\omega_1=\omega_0\cos(\Omega t)$$
és
$$\omega_2=\omega_0\sin(\Omega t)$$
Mivel $\omega_3$ állandó, $N_3={\Theta}_3\omega_3$ is állandó. Tegyük fel, hogy
az impulzusmomentum vektora a $z$ irányba mutat. Ekkor $N_3=N\cos\vartheta$,
tehát a mozgás során $\vartheta$ is állandó, így $\dot{\vartheta}=0$. A
precesszió szögsebessége (az $x$, $y$, $z$ rendszerben)
$$\dot{\varphi}=\frac{\sqrt{\omega_1^2+\omega_2^2}}{\sin\vartheta}=\frac{N\sin\vartheta}{{\Theta}_1\sin\vartheta}= \frac{N}{{\Theta}_1}$$
A fő tehetetlenségi tengelyek $x_1$, $x_2$, $x_3$ koordinátarendszerében mind
az $\bf \omega$ szögsebességvektor, mind az $\bf N$ impulzusmomentum-vektor
$\Omega$ szögsebességgel forog az $x_3$ szimmetriatengely körül.
Egy pontjában rögzített súlyos szimmetrikus pörgettyű
mozgása

$$L=\frac{1}{2}\left({\Theta}_1+ml^2\right)\left(\dot{\vartheta}^2+\dot{\varphi}^2\sin^2\vartheta\right)+\frac{1}{2}{\Theta}_3\left(\dot{\varphi}\cos\vartheta+\dot{\psi}\right)^2-mgl\cos\vartheta$$
Megmaradó mennyiségek:
- Az impulzusmomentum $z$-komponense:
$$\frac{d}{dt}\frac{\partial L}{\partial \dot{\varphi}}=\frac{\partial L}{\partial
\varphi}=0\quad \Rightarrow \quad N_z\equiv p_\varphi=\frac{\partial L}{\partial
\dot{\varphi}}=\left({\Theta}_1+ml^2\right)\dot{\varphi}\sin^2\vartheta+{\Theta}_3\left(\dot{\varphi}\cos\vartheta+\dot{\psi}\right)\cos\vartheta={\rm állandó}$$
- Az impulzusmomentum $x_3$-komponense:
$$\frac{d}{dt}\frac{\partial L}{\partial \dot{\psi}}=\frac{\partial L}{\partial
\psi}=0\quad \Rightarrow \quad N_3\equiv p_\psi=\frac{\partial L}{\partial
\dot{\psi}}={\Theta}_3\left(\dot{\varphi}\cos\vartheta+\dot{\psi}\right)={\rm állandó}$$
- Az energia:
$$E=\dot{\vartheta}\frac{\partial L}{\partial
\dot{\vartheta}}+\dot{\varphi}\frac{\partial L}{\partial
\dot{\varphi}}+\dot{\psi}\frac{\partial L}{\partial
\dot{\psi}}-L=\frac{1}{2}\left({\Theta}_1+ml^2\right)\left(\dot{\vartheta}^2+\dot{\varphi}^2\sin^2\vartheta\right)+\frac{1}{2}{\Theta}_3\left(\dot{\varphi}\cos\vartheta+\dot{\psi}\right)^2+mgl\cos\vartheta$$
$N_z$ és $N_3$ megmaradásából következik, hogy
$$\dot{\varphi}=\frac{N_z-N_3\cos\vartheta}{\left({\Theta}_1+ml^2\right)\sin^2\vartheta}$$
és
$$\dot{\psi}=\frac{N_3}{{\Theta}_3}-\frac{N_z-N_3\cos\vartheta}{\left({\Theta}_1+ml^2\right)\sin^2\vartheta}\cos\vartheta$$
valamint
$$E=\frac{1}{2}\left({\Theta}_1+ml^2\right)\dot{\vartheta}^2+\frac{\left(N_z-N_3\cos\vartheta\right)^2}{2\left({\Theta}_1+ml^2\right)\sin^2\vartheta}+\frac{N_3^2}{2{\Theta}_3}+mgl\cos\vartheta$$
Legyen
$$E'=E-\frac{N_3^2}{2{\Theta}_3}\;,$$
$${\Theta}_1'={\Theta}_1+ml^2$$
és
$$V_{eff}(\vartheta)=\frac{\left(N_z-N_3\cos\vartheta\right)^2}{2{\Theta}_1'\sin^2\vartheta}+mgl\cos\vartheta$$
Ekkor
$$E'=\frac{1}{2}{\Theta}_1'\dot{\vartheta}^2+V_{eff}(\vartheta)$$
adódik. A súlyos, szimmetrikus pörgettyű mozgását tehát egydimenziós feladatra
lehetett visszavezetni.
Biciklikerék (súlyos pörgettyű)
Giroszkóp
Szimmetrikus pörgettyű
tengelye az erőre merőlegesen fordul el.


 bene@arpad.elte.hu
bene@arpad.elte.hu




