


Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
11. hét keddi előadás
Egy pontjában rögzített súlyos szimmetrikus pörgettyű
mozgása (folytatás)
Megmaradó mennyiségek: $N_z$, $N_3$, $E$.
$$E'=\frac{1}{2}{\Theta}_1'\dot{\vartheta}^2+\underbrace{\frac{\left(N_z-N_3\cos\vartheta\right)^2}{2{\Theta}_1'\sin^2\vartheta}+mgl\cos\vartheta}_{V_{eff}(\vartheta)}$$
$\begin{eqnarray}
{\Theta}_1'\ddot{\vartheta}&=& -\frac{\partial
V_{eff}}{\partial\vartheta}=-N_3\frac{N_z-N_3\cos\vartheta}{{\Theta}_1'\sin\vartheta}+\frac{\left(N_z-N_3\cos\vartheta\right)^2\cos\vartheta}{{\Theta}_1'\sin^3\vartheta
}+mgl\sin\vartheta\;,\\
\dot{\varphi}&=& \frac{N_z-N_3\cos\vartheta}{{\Theta}_1'\sin^2\vartheta}\;,\\
\dot{\psi}&=& \frac{N_3}{{\Theta}_3}-\frac{N_z-N_3\cos\vartheta}{{\Theta}_1'\sin^2\vartheta}\cos\vartheta\;,
\end{eqnarray}$
ahol
$$E'=E-\frac{N_3^2}{2{\Theta}_3}\;,$$
$${\Theta}_1'={\Theta}_1+ml^2\;.$$
Az $x_3$ szimmetriatengely irányát meghatározó térbeli polárszögek $\vartheta$ és $\varphi-\pi/2$.
Súlyos szimmetrikus
pörgettyű mozgása (Java-animáció)
Biciklikerék (súlyos pörgettyű)
Giroszkóp
Szimmetrikus pörgettyű
tengelye az erőre merőlegesen fordul el.
Mikor stabil a függőleges szimmetriatengelyű forgás?
Természetesen akkor, ha a $V_{eff}(\vartheta)$ effektív potenciálnak
lokális minimuma van $\vartheta=0$-ban. A $\vartheta=0$ esetben $N_z=N_3=N$,
így $\vartheta\ll 1$ esetén
$
\begin{eqnarray}
V_{eff}(\vartheta)&=&
\frac{N^2}{2{ \Theta}_1'}\frac{\left(1-\cos\vartheta\right)^2}{\sin^2\vartheta}+mgl\cos\vartheta=\frac{N^2}{2{ \Theta}_1'}\frac{4\sin^2\left(\frac{\vartheta}{2}\right)}{4\sin^2\left(\frac{\vartheta}{2}\right)\cos^2\left(\frac{\vartheta}{2}\right)}+mgl\cos\vartheta=\frac{N^2}{2{ \Theta}_1'}\frac{1}{\cos^2\left(\frac{\vartheta}{2}\right)}+mgl\cos\vartheta\\
&\approx&\frac{N^2}{2{ \Theta}_1'}\frac{1}{\left(1-\frac{\vartheta^2}{8}\right)^2}+mgl\left(1-\frac{\vartheta^2}{2}\right)\approx
\frac{N^2}{2{ \Theta}_1'}+mgl +\frac{1}{2}mgl\vartheta^2\left(\frac{N^2}{4{ \Theta}_1'mgl}-1\right)
\end{eqnarray}
$
A minimum feltétele tehát
$$\frac{N^2}{4{\Theta}_1'mgl}>1$$
vagy másképp
$$\frac{{\Theta}_3^2\omega^2}{4\left({\Theta}_1+ml^2\right)mgl}>1$$
ill.
$$\omega>2\sqrt{\frac{\left({\Theta}_1+ml^2\right)ml^2}{{\Theta}_3^2}}\sqrt{\frac{g}{l}}$$
Fizikai inga
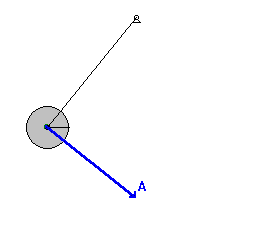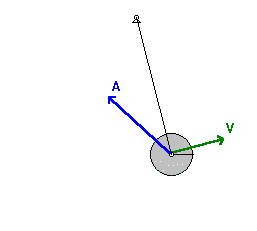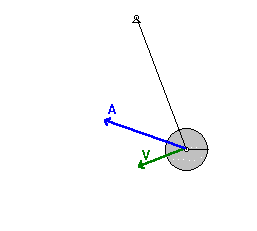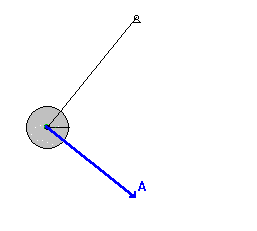
$$N_z=N_3=0\;\Rightarrow\;\dot{\varphi}=\dot{\psi}=0$$
$$L=\frac{1}{2}\left({\Theta}_1+ml^2\right)\dot{\vartheta}^2-mgl\cos\vartheta$$
$$E=\frac{1}{2}\left({\Theta}_1+ml^2\right)\dot{\vartheta}^2+mgl\cos\vartheta$$
Súlyos szimmetrikus pörgettyű precessziója: alkalmazás a
Föld forgására
A forgatónyomaték eredete: árapálykeltő erők hatnak a nem tökéletesen
gömbszimmetrikus Földre.
Vizsgáljuk a Hold-Föld rendszert. Az égitestek pályáját körnek tekintjük.
A Föld egy $dm$ tömegelemére ható eredő erő:
$$d{\bf F}=-G\frac{m_{Hold}dm}{|{\bf r}-{\bf R}|^3}({\bf r}-{\bf R})\approx -G\frac{m_{Hold}dm}{R^3}\left({\bf r}-{\bf R}+3{\bf n}({\bf r}\cdot{\bf n})\right)$$
Itt $\bf R$ a Föld középpontjából a Hold középpontjába mutató helyvektor, $\bf
r$ a $dm$ tömegelem helyvektora a Föld középpontjától mérve, valamint
$${\bf n}=\frac{{\bf R}}{R}$$
A közös tömegközéppont körüli körmozgásból:
$$\left(\frac{2\pi}{T_{hó}}\right)^2=G\frac{m_{Hold}+m_{Föld}}{R^3}$$
következik. Ezzel
$\begin{eqnarray}
d{\bf F}&=& -dm
\left(\frac{2\pi}{T_{hó}}\right)^2\frac{m_{Hold}}{m_{Hold}+m_{Föld}} \left({\bf r}-{\bf R}+3{\bf n}({\bf r}\cdot{\bf n})\right)
\end{eqnarray}$
Ennek a Föld tömegközéppontjára vonatkozó forgatónyomatéka
$$d{\bf M}={\bf r}\times d{\bf F}=dm
\left(\frac{2\pi}{T_{hó}}\right)^2\frac{m_{Hold}}{m_{Hold}+m_{Föld}}
\left({\bf r}\times{\bf R}+3({\bf r}\cdot{\bf n})({\bf n}\times{\bf r})\right)$$
A Föld térfogatára integrálva kapjuk a teljes forgatónyomatékot. A
Földet homogén forgási ellipszoidnak tekintjük, az egyenlítői sugár $a=6378\;km$, a
sarki féltengely hossza $b=6357\; km$.
$$\int dV {\bf r}{\bf r}^T=\frac{1}{5}V\left(a^2({\bf e}_1{\bf e}_1^T+{\bf
e}_2{\bf e}_2^T)+b^2{\bf e}_3{\bf e}_3^T\right)$$
Itt $\bf e_3$ a Föld tengelye (egységvektor), az $\bf e_1$, $\bf
e_2$ egységvektor két erre merőleges irány.
A mozgás során az $\bf n$ irány a teljes impulzusmomentum változásához képest
gyors egyenletes körmozgást végez, ezért a forgatónyomatékot a főtengelyek
változatlan helyzete mellett egy teljes keringésre átlagoljuk. Eredmény:
$\begin{eqnarray}
{\bf M}&=&
\frac{1}{5}m_{Föld}\left(\frac{2\pi}{T_{hó}}\right)^2\frac{m_{Hold}}{m_{Hold}+m_{Föld}}\frac{3}{2}
\left[ a^2({\bf e}_1\cdot{\bf e}_z)({\bf e}_z\times{\bf e}_1)
+a^2({\bf e}_2\cdot{\bf e}_z)({\bf e}_z\times{\bf e}_2)
+b^2({\bf e}_3\cdot{\bf e}_z)({\bf e}_z\times{\bf e}_3) \right]
\end{eqnarray}$
Ez azt jelenti, hogy az egy keringési időre átlagolt forgatónyomaték a
keringés síkjával párhuzamos, a Föld tengelyére merőleges, nagysága pedig
$$|{\bf
M}|=\frac{3}{2}\frac{m_{Hold}}{m_{Hold}+m_{Föld}}\left(\frac{2\pi}{T_{hó}}\right)^2\frac{1}{5}m_{Föld}(a^2-b^2)\sin\beta\cos\beta$$
ahol $\beta=23,4^\circ$ a Föld tengelyének a keringés síkjának normálisával
bezárt szöge. (Ténylegesen a Hold keringési síkja kis szöget zár be az
ekliptikával, ezt itt elhanyagoljuk.)
A Nap járuléka ugyanilyen irányú, $m_{Hold}\;\rightarrow\;m_{Nap}$ és
$T_{hó}\;\rightarrow\;T_{év}$ helyettesítéssel kapható meg. Az együttes
forgatónyomaték nagysága
$$|{\bf
M}|=\frac{3}{2}\left(\frac{m_{Hold}}{m_{Hold}+m_{Föld}}\left(\frac{2\pi}{T_{hó}}\right)^2+\frac{m_{Nap}}{m_{Nap}+m_{Föld}}\left(\frac{2\pi}{T_{év}}\right)^2\right)\frac{1}{5}m_{Föld}(a^2-b^2)\sin\beta\cos\beta$$
A precesszió periódusideje:
$$T_{pr}|{\bf M}|=2\pi { \Theta}_3\omega_3 \sin\beta$$
Itt
$$\omega_3=\frac{2\pi}{T_{nap}}$$
és
$$\Theta_3=\frac{2}{5}m_{Föld}a^2$$
Ezzel
$
\begin{eqnarray}
T_{pr}&=& \frac{2}{3}\frac{1}{\cos\beta}\frac{a}{a-b}\frac{1}{T_{nap}\left(\frac{m_{Hold}}{m_{Hold}+m_{Föld}}\left(\frac{1}{T_{hó}}\right)^2+\frac{m_{Nap}}{m_{Nap}+m_{Föld}}\left(\frac{1}{T_{év}}\right)^2\right)}\\
&\approx &
\frac{2}{3}\frac{1}{\cos\beta}\frac{a}{a-b}\frac{T_{év}}{T_{nap}}\frac{1}{1+\frac{m_{Hold}}{m_{Föld}}\left(\frac{T_{év}}{T_{hó}}\right)^2}T_{év}=28500\;év
\end{eqnarray}$
A pontosabb érték 25900 év.


 bene@arpad.elte.hu
bene@arpad.elte.hu
