


Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
11. hét pénteki előadás
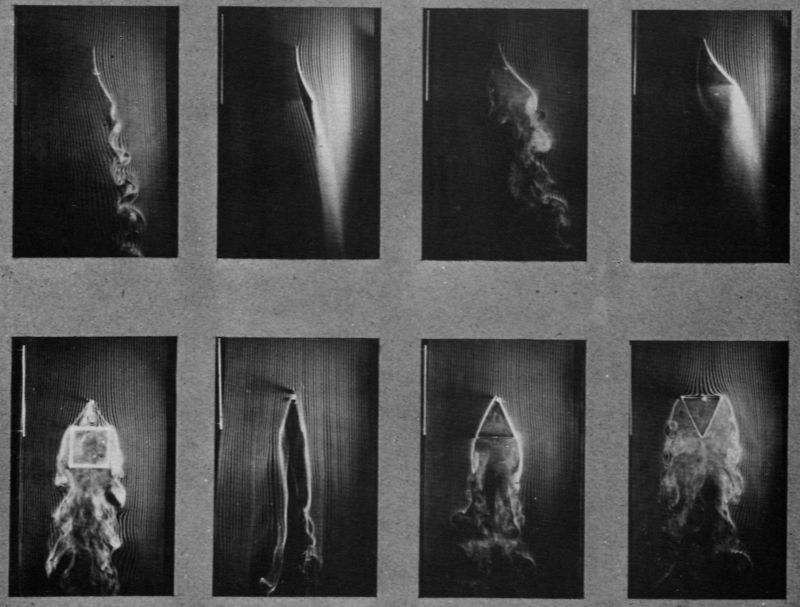
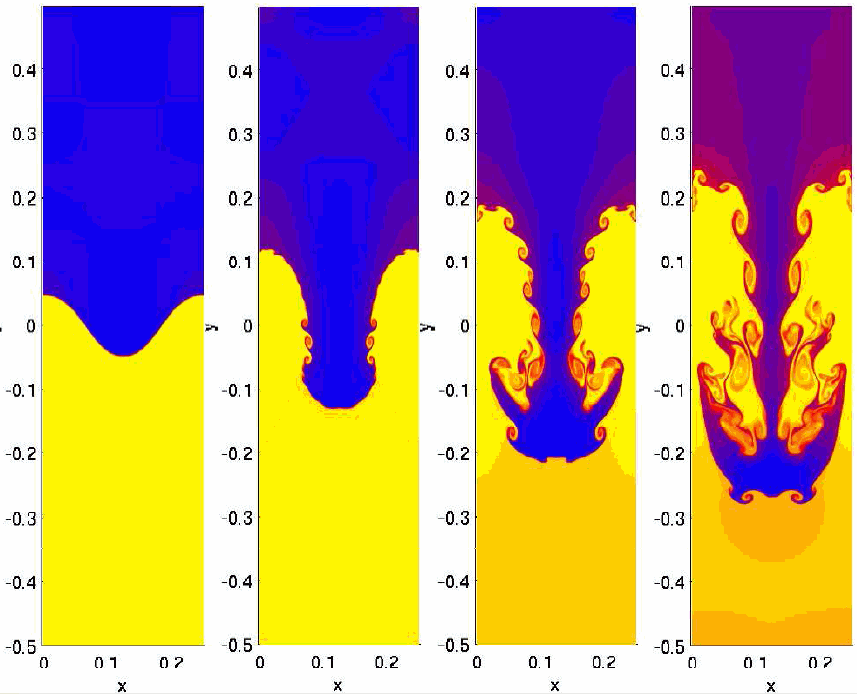







 Légy
Légy
1.1. Bevezetés
-
Folyadékok és gázok mechanikája: a Newton-törvények alkalmazása folytonos közegekre
-
Fenomenológiai leírás: folytonosnak tekintett közegek, a különböző
anyagok csak állapotegyenletükben és anyagi állandóikban
különböznek. Nem vizsgáljuk a mikroszkopikus hátteret.
A közegbeli hangsebességhez képest kis áramlási sebességek esetén a
gázok is jó közelítéssel összenyomhatatlanok.
-
-
Térmennyiségek:
sebesség:
$$ {\bf v}({\bf r}, t) $$
sűrűség:
$$\rho({\bf r}, t)$$
nyomás:
$$p({\bf r}, t)$$
Az állapotegyenletből a
$T({\bf r}, t)$
hőmérséklet már következik.
-
Lokális egyensúly feltételezése: az anyag kis térfogatában áramlás
közben is ugyanazok a termodinamikai összefüggések teljesülnek, mint
termodinamikai egyensúlyban.
1.2. Hidrosztatika
-
Folytonos közegben ható erők:
-
tömegerők (a közeg minden részében hatnak, kis folyadékrész esetén a tömeggel arányosak):
$$d{\bf F}=\rho {\bf f}dV$$
Itt ${\bf f}$ az erősűrűség. Pl. gravitációs térben ${\bf f}={\bf g}$, ahol ${\bf g}$ a nehézségi gyorsulás.
-
felületi erők (a szomszédos folyadékrészek között ható rövid hatótávolságú erők, pl. van der Waals-erők, eredetük: elektrosztatikus + kicserélődési kölcsönhatás a Pauli-elvnek megfelelően):
-
Arányosak a felülettel.
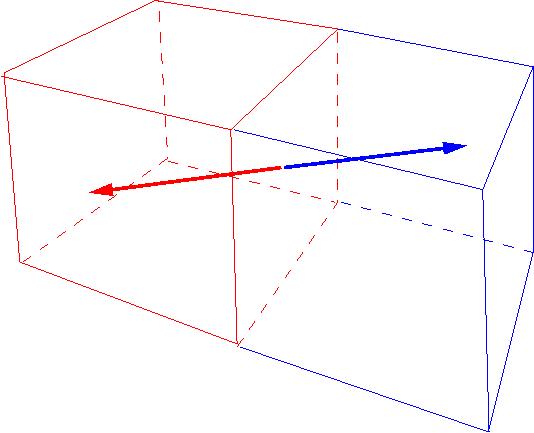
-
Húzó és nyomóerők: a felület normálisának irányába mutatnak
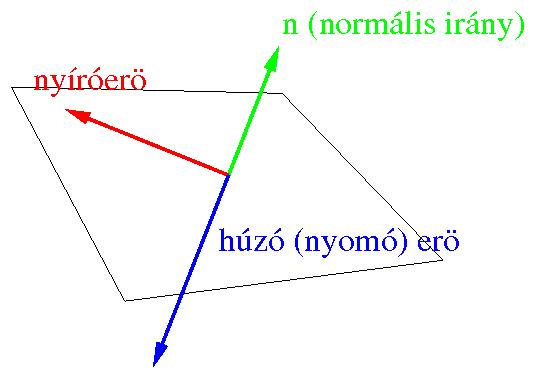
-
Nyíróerők: a felület normálisára merőleges irányba mutatnak
-
Általában:
$$d{\bf F}={\cal \sigma}{\bf n}dA$$
Itt ${\cal \sigma}$ a feszültségtenzor
Mátrixjelöléssel:
$$\left(\begin{array}{c}F_x\\F_y\\F_z\end{array}\right)=\left(\begin{array}{ccc}\sigma_{xx}&\sigma_{xy}&\sigma_{xz}\\\sigma_{yx}&\sigma_{yy}&\sigma_{yz}\\\sigma_{zx}&\sigma_{zy}&\sigma_{zz}\end{array}\right)\left(\begin{array}{c}n_x\\n_y\\n_z\end{array}\right)dA$$
azaz
$\begin{eqnarray}
F_x&=&\sigma_{xx}n_x dA+\sigma_{xy}n_y dA+\sigma_{xz}n_z dA\\
F_y&=&\sigma_{yx}n_x dA+\sigma_{yy}n_y dA+\sigma_{yz}n_z dA\\
F_z&=&\sigma_{zx}n_x dA+\sigma_{zy}n_y dA+\sigma_{zz}n_z dA
\end{eqnarray}$
Eszerint pl. $\sigma_{zy}$ az $y$ irányba mutató normálisú egységnyi felületelemre ható erő $z$ komponense.
-
Nyugvó folyadékban ill. gázban nyíróerők nem lépnek fel (Pascal
törvénye).
$$\left(\begin{array}{ccc}\sigma_{xx}&\sigma_{xy}&\sigma_{xz}\\\sigma_{yx}&\sigma_{yy}&\sigma_{yz}\\\sigma_{zx}&\sigma_{zy}&\sigma_{zz}\end{array}\right)
=\left(\begin{array}{ccc}-p&0&0\\0&-p&0\\0&0&-p\end{array}\right)$$
-
Áramlás közben valódi folyadékban fellépnek nyíróerők. Oka: belső súrlódás.
-
Ideális folyadék: belső súrlódás elhanyagolható, áramlás közben sem
lépnek fel benne nyíróerők.
-
Egyensúlyban a felületi erő
$$d{\bf F}=-p {\bf n}dA$$
-
Az egyensúly feltétele:
- Tetszőleges térfogatra az eredő erő zérus:
$$\int \rho {\bf f} dV - \oint p dA =0$$
- Differenciális alak:
x komponens:
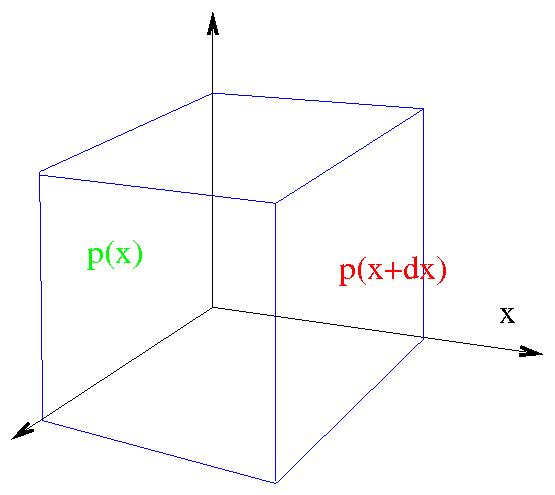 $$\rho f_x \Delta x \Delta y \Delta z -\left(p(x+\Delta
x)-p(x)\right)\Delta y \Delta z=0$$
$$\rho f_x-\frac{\partial p}{\partial x}=0$$
$$\rho f_x \Delta x \Delta y \Delta z -\left(p(x+\Delta
x)-p(x)\right)\Delta y \Delta z=0$$
$$\rho f_x-\frac{\partial p}{\partial x}=0$$
- Vektoralakban:
$$\rho {\bf f}-grad\; p=0$$
$$\rho {\bf f}-{\bf \nabla} p=0$$
$${\bf f}-\frac{1}{\rho}{\bf \nabla} p=0$$
A hidrosztatikában ${\bf v}({\bf r},t)=0$. A fenti egyenlet kapcsolat $\rho({\bf r})$ és $p({\bf r})$ között. Ehhez jön még az állapotegyenlet.
- Következmények:
- Konzervatív tömegerő:
$${\bf f} = -{\bf \nabla} U \;\rightarrow\; \rho {\bf \nabla} U+{\bf \nabla}
p = 0$$
Az ekvipotenciális felületek és az izobárok egybeesnek.
- Barotróp folyadék:
$$\rho=\rho(p)$$
pl. összenyomhatatlan folyadék, izoterm folyadék, adiabatikus
folyadék.
$$\frac{p}{\rho}=\frac{R}{M}T$$
$$\frac{p}{\rho^\kappa}=const.$$
Az egyensúlyi egyenletet integrálva:
$$U+\int_{p_0}^{p}\frac{dp'}{\rho(p')}=const.$$
nyomásfüggvény:
$$P(p)=\int_{p_0}^{p}\frac{dp'}{\rho(p')}$$
Egyensúlyban tehát $U+P=const.$
- Egyensúly nehézségi erőtérben:
$$\frac{\partial p}{\partial z}=-\rho g\;,\frac{\partial p}{\partial x}=\frac{\partial p}{\partial y}=0\;$$
ha a $z$-tengely ${\bf g}$-vel párhuzamos. Következmény: $\rho$, $p$, $T$ csak $z$-től függ.
- Összenyomhatatlan folyadék:
$$\rho_0 g z+p=p_0$$
$p$, $T$ lineáris függvénye a magasságnak.
- Barométeres magasságformula izotermikus ideális gázra:
$$P(p)=\int_{p_0}^{p}\frac{dp'}{p'}\frac{RT_0}{M}=\frac{RT_0}{M}\ln
\frac{p}{p_0}$$
$$P+U=const.$$
$$p=p_0\;\exp \left(-\frac{Mg}{RT_0}z\right)$$
- Adiabatikus ideális gáz:
$$\rho=\rho_0 \left(\frac{p}{p_0}\right)^{1/\kappa}$$
$$\int_{p_0}^{p}\frac{dp'}{\rho_0(p'/p_0)^{1/\kappa}}=\frac{p_0^{1/\kappa}}{\rho_0}\frac{\kappa}{\kappa-1}\left(p^{\frac{\kappa-1}{\kappa}}-p_0^{\frac{\kappa-1}{\kappa}}\right)=-gz$$
$$p=p_0\left(1-\frac{\kappa-1}{\kappa}\frac{\rho_0}{p_0}gz\right)^{\frac{\kappa}{\kappa-1}}$$
$\kappa\rightarrow 1$-re
$$p=p_0{\rm e}^{-\frac{\rho_0}{p_0}gz}$$
- Ismert hőmérsékleteloszlású ideális gáz:
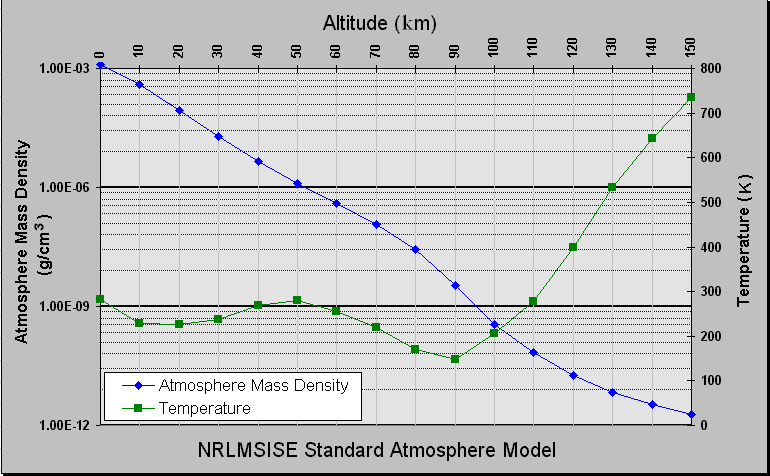 $$\frac{dp}{dz}=-\rho g = -\frac{Mg}{RT(z)}p$$
$$\frac{dp}{p}= -\frac{Mg}{RT(z)}dz$$
$$\ln \frac{p}{p_0}=-\frac{Mg}{R}\int_{z_0=0}^z\frac{dz'}{T(z')}$$
$$\frac{dp}{dz}=-\rho g = -\frac{Mg}{RT(z)}p$$
$$\frac{dp}{p}= -\frac{Mg}{RT(z)}dz$$
$$\ln \frac{p}{p_0}=-\frac{Mg}{R}\int_{z_0=0}^z\frac{dz'}{T(z')}$$
1.3. Áramlások leírása
-
Áramvonal: pillanatfelvétel a sebességtérről
-
Stacionárius áramlás: ${\bf v}$, $\rho$, $p$ időtől független
-
Pályavonal: egy kiszemelt kis folyadékrész pályája
Stacionárius áramlás esetén megegyezik az áramvonallal.
-
Változások
- lokális változások: adott helyen a térmennyiség változása, pl.
$$\frac{\partial \rho}{\partial t}$$
- szubsztanciális változások: egy kiszemelt kis folyadékrészt
mozgásában követünk, eközben vizsgáljuk a térmennyiség változását
sűrűség:
$$d\rho= \rho(x+v_xdt,y+v_ydt,z+v_zdt,t+dt)-\rho(x,y,z,t)$$
$$\approx
\left(\frac{\partial \rho}{\partial x}v_x+\frac{\partial \rho}{\partial y}v_y+\frac{\partial \rho}{\partial z}v_z+\frac{\partial \rho}{\partial t}\right) dt$$
$$\frac{d\rho }{dt}=\frac{\partial \rho}{\partial
t}+{\bf v}grad \rho$$
sebesség:
$$\frac{d{\bf v} }{dt}=\frac{\partial {\bf v}}{\partial
t}+\left({\bf v}grad\right) {\bf v}$$
-
Anyagmegmaradás: kontinuitási egyenlet
Felületelemen időegység alatt átáramló tömeg:
$$\rho {\bf v}{\bf n}dA=\rho
{\bf v}d{\bf A}$$
megmaradás:
$$-\frac{d}{dt}\int \rho dV=\oint \rho {\bf v}d{\bf A}$$
Gauss-tétele szerint:
$$\int\left(\frac{\partial \rho}{\partial t}+div(\rho
{\bf v})\right)dV=0$$
$$\frac{\partial \rho}{\partial t}+div(\rho
{\bf v})=0$$
$$\frac{d \rho}{d t}=-\rho div{\bf v}$$
-
$div\; {\bf v}$ és $rot\; {\bf v}$ jelentése:
$div{\bf v}$ a sűrűség szubsztanciális változását jellemzi. Összenyomhatatlan folyadékban $$\frac{d \rho}{d t}=0\;\rightarrow\;div\; {\bf v}=0$$
$rot\;{\bf v}$ a folyadékelem forgó mozgását jellemzi.
Pl. merev testként forgó folyadék sebességtere:
$$\bf v=\bf \omega \times \bf r$$
$$rot \; \bf v=2\bf \omega$$
Általában az $\bf \Omega =\frac{1}{2} rot\; \bf v$ örvényvektor a lokális szögsebesség vektora.
$$div \; {\bf v}\;
=\;{\bf \nabla}{\bf v}\;=\;\frac{\partial v_x}{\partial
x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}$$
$$rot\; {\bf v}\;
=\;{\bf \nabla}\;\times\;{\bf v}\;=\;\left(\begin{array}{l}
\frac{\partial v_z}{\partial
y}-\frac{\partial v_y}{\partial z}\\
\frac{\partial v_x}{\partial
z}-\frac{\partial v_z}{\partial x}\\
\frac{\partial v_y}{\partial
x}-\frac{\partial v_x}{\partial y}
\end{array}\right)$$
2.2. Ideális folyadék mozgásegyenletei
Ideális folyadék: irreverzibilis folyamatok (belső súrlódás, hővezetés)
nincsenek (valódi folyadékra jó közelítés lehet) $\rightarrow$ nincsenek
nyíróerők.
-
Euler-egyenlet (mozgásegyenlet)
a $\Delta V$ térfogatú folyadékrészre, mivel a felületi erő $-pd{\bf F}$ (mint a
sztatikában)
$$\rho\; \Delta V\; \frac{d{\bf v}}{dt}=\rho\; {\bf f}\;\Delta V
- grad\; p\; \Delta V$$
$$\frac{\partial {\bf v}}{\partial t}+({\bf v} \;grad){\bf v}={\bf f}\;
- \frac{1}{\rho}\;grad\; p$$
Nemlineáris parciális differenciálegyenlet + határfeltételek
-
Kontinuitási egyenlet
$$\frac{\partial \rho}{\partial t}+div(\rho
{\bf v})=0$$
-
Az ötödik egyenlet (egy pályavonal mentén):
$$\frac{ds}{dt}=0$$
Itt $s$ a fajlagos entrópia, $s=S/m$, vagyis a tömegegységre eső entrópia.
Abból következik, hogy ideális folyadékban nincs belső súrlódás és hőcsere,
valamint lokális termodinamikai egyensúly áll fent, azaz kis folyadékelem
állapotváltozása egyensúlyi állapotokon keresztül történik.
Ha kezdetben az entrópia mindenütt azonos (tipikus eset), akkor $s=const.$
(helytől függetlenül)
$s$ általában $\rho$ és $p$ függvénye (állandó összetételű
folyadékot
feltételezve). $s(\rho,p)=const.$ adiabatikus állapotegyenlet $\rightarrow$ a
folyadék barotróp.
$p/\rho^\kappa=állandó$ egy pályavonal mentén.
$\kappa=\frac{c_p}{c_v}$
-
Következmény: a folyadékrész belső energiája csak a térfogati munka révén
változik
$$d\epsilon =Tds-pd\left(\frac{1}{\rho}\right)=Tds+\frac{p}{\rho^2}d\rho$$
$$\frac{d\epsilon}{dt}=\frac{p}{\rho^2}\frac{d\rho}{dt}=-\frac{p}{\rho}div
\;{\bf v}$$
Összenyomhatatlan folyadék esetén $\epsilon=áll.$
2.3. A Bernoulli-egyenlet - munkatétel
-
Előkészítés:
-
$$({\bf v}\;grad){\bf v}=grad\;\frac{v^2}{2}-{\bf v}\times rot
\;{\bf v}$$
$\begin{eqnarray}
({\bf v}\times rot
\;{\bf v})_x\;&=&\;v_y\left(\partial_xv_y-\partial_yv_x\right)-v_z\left(\partial_zv_x-\partial_xv_z\right)\\
\;&=&\;
v_x\partial_xv_x+v_y\partial_xv_y+v_z\partial_xv_z-v_x\partial_xv_x-v_y\partial_yv_x-v_z\partial_zv_x
\end{eqnarray}$
-
Fajlagos entalpia:
$$w=\epsilon+\frac{p}{\rho}$$
$$dw=\underbrace{d\epsilon-\frac{p}{\rho^2}d\rho}_{\text{$=0$, mert $ds=0$}}+\frac{1}{\rho}dp$$
$$dw=\frac{1}{\rho}dp$$
$$w=\int \frac{dp}{\rho}\;,$$
ahol $\rho(p)$ az adiabatikus állapotváltozásnak felel meg. $w$ tehát az
"adiabatikus nyomásfüggvény".
$$grad\; w=\frac{1}{\rho}grad\;p$$
-
Stacionárius áramlás konzervatív tömegerővel
Euler-egyenlet:
$$({\bf v}\;grad){\bf v}=-grad\; V\;-\underbrace{\frac{1}{\rho}grad\; p}_{grad\; w}$$
$$grad\;\frac{v^2}{2}-\underbrace{{\bf v}\times rot
\;{\bf v}}_{\perp \;{\bf v}\rm{-re} }+grad\; V\;+grad\; w=0\quad \left/\; \cdot {\bf v} \right.$$
$${\bf v}\cdot grad\left(\frac{v^2}{2}+V+w\right)=0$$
${\bf v}\cdot grad$ a sebesség irányú derivált.
Az egyenlet tehát azt jelenti, hogy $$\frac{v^2}{2}+V+w= állandó\quad\quad \text{(Bernoulli-egyenlet)}$$ az
áramvonal mentén (ami most egybesik a pályavonallal).
Munkatétel: egy folyadékrészecskére
$$\frac{v_2^2}{2}+V_2-\left(\frac{v_1^2}{2}+V_1\right)=\underbrace{-\int_1^2\frac{1}{\rho}\underbrace{grad\;p\;\cdot
d{\bf s}}_{dp}}_{\text{A felületi erő munkája}}=\underbrace{-\int_{p_1}^{p_2}\frac{dp}{\rho}}_{-w_2+w_1}$$

-
Összenyomhatalan folyadékra, külső erő nélkül
$$\frac{v^2}{2}+\frac{p}{\rho_0}=\frac{p_0}{\rho_0}$$
$$\underbrace{\frac{1}{2}\rho_0v^2}_{\text{torlónyomás}}+p=p_0$$
Mivel $p>0$
$$v^2\le \frac{2 p_0}{\rho_0}$$
egyébként buborékképződés, kavitáció.
-
Örvénymentes áramlások
- Örvénymentes: $$rot {\bf v}=0$$ mindenütt az áramlási térben.
Ekkor létezik a $\Phi({\bf r},t)$ sebességpotenciál, melyre
$${\bf v}=grad\;\Phi$$
Legyen a tömegerő konzervatív, és tegyük fel, hogy $s=konst.$, tehát
$\frac{1}{\rho}grad\;p=grad\;w$ minden pontban.
Az Euler-egyenlet ekkor
$$\underbrace{\frac{\partial {\bf v}}{\partial
t}}_{grad \frac{\partial \Phi}{\partial
t}}+grad\;\frac{v^2}{2}-{\bf v}\times \underbrace{rot \;
{\bf v}}_{=0}=-grad\;V-grad\;w$$
$$grad\left(\frac{\partial \Phi}{\partial
t}+\frac{v^2}{2}+V+w\right)=0$$
azaz
$$\frac{\partial \Phi}{\partial
t}+\frac{v^2}{2}+V+w=F(t)$$
ahol $F(t)$ csak az időtől függ.
Ha a tömegerő nem konzervatív, vagy a folyadék nem barotróp (pl. mert $s$
nem állandó), akkor általában nem létezik örvénymentes áramlás.
- Stacionárius eset
$$\frac{\partial \Phi}{\partial
t}=0\quad\Rightarrow\quad F(t)=\text{állandó}\quad\Rightarrow\quad
\frac{v^2}{2}+V+w=\text{állandó az egész térben.}$$
Általánosabb, mint a Bernoulli-egyenlet.
-
Összenyomhatatlan folyadék örvénymentes áramlása
$$\left.\begin{array}{l}
div {\bf v}=0\\
rot {\bf v}=0
\end{array}\right\}\Rightarrow \triangle \Phi=0\quad +\text{határfeltételek}$$
Az egyenlet meghatározza a sebességteret. Az időfüggés csak a
határfeltételekben jelentkezik.
A nyomás a
$$\frac{\partial \Phi}{\partial
t}+\frac{v^2}{2}+V+\frac{p}{\rho}=F(t)$$
egyenletből számolható ($F$ beleolvasztható $\frac{\partial \Phi}{\partial
t}$-be). A nemlinearitás csak itt jelentkezik.
- Stacionárius eset
$$\frac{p}{\rho}=konst.-V-\frac{v^2}{2}$$
-
Példák sebeségpotenciálra:
$$\Phi={\bf v}_0\cdot {\bf r}\Rightarrow
{\bf v}({\bf r},t)=grad \Phi={\bf v}_0$$
$$\Phi=-\frac{Q}{4\pi}\frac{1}{r}\Rightarrow
{\bf v}({\bf r},t)=grad \Phi=\frac{Q}{4\pi}\frac{1}{r^2}\frac{{\bf r}}{r}$$
3.2. Örvénymentes áramlások (folytatás)
-
Cirkuláció örvénymentes áramlásban:
Adott C görbére:
$$\Gamma_C=\oint_C {\bf v}\cdot d{\bf s}$$
Ha a C zárt görbére fektethető olyan felület, amely teljesen az áramlás
tartományában van, akkor
$$\Gamma_C=\oint_C {\bf v}\cdot d {\bf s}=\int rot
{\bf v} \cdot d {\bf F}=0$$
Felhasználtuk Stokes tételét.
Az ilyen tulajdonságú görbék a folyadék belsejében folytonos deformációval
egy ponttá húzhatók össze. Ha ez minden zárt görbére teljesül, akkor azt
mondjuk, hogy a tartomány (jelen esetben az áramlási tér)
egyszeresen összefüggő.
3.3. Síkbeli áramlások
-
Síkbeli áramlás:
az áramlás jellemzői a $z$ tengelyre merőleges síkban azonosak, semmi nem függ
$z$-től. $\Phi=\Phi(x,y)$
$$\frac{\partial^2 \Phi}{\partial x^2}+\frac{\partial^2 \Phi}{\partial y^2}=0$$
Komplex potenciál és sebesség:
$$z=x+iy$$
Itt $z$ nem a $z$ koordináta, hanem egy komplex szám!
$$f(z)=\Phi(x,y)+i\Psi(x,y)$$
$$\frac{df}{dx}=\frac{\partial \Phi}{\partial x}+i\frac{\partial \Psi}{\partial
x}=\frac{df}{dz}\quad y=konst.$$
$$\frac{df}{idy}=-i\frac{\partial \Phi}{\partial y}+\frac{\partial
\Psi}{\partial y}=\frac{df}{dz}\quad x=konst.$$
$$\frac{\partial \Phi}{\partial x}=\frac{\partial
\Psi}{\partial y}\quad \text{és}\quad\frac{\partial \Phi}{\partial y}=-\frac{\partial
\Psi}{\partial x} $$
Cauchy-Riemann-feltételek.
Következmény:
$$\frac{\partial^2 \Phi}{\partial x^2}=\frac{\partial^2
\Psi}{\partial x\partial y}\quad ,\quad\frac{\partial^2 \Phi}{\partial y^2}=-\frac{\partial^2
\Psi}{\partial y\partial x} \Rightarrow \frac{\partial^2 \Phi}{\partial
x^2}+\frac{\partial^2 \Phi}{\partial y^2}=0\quad ,\quad \frac{\partial^2 \Psi}{\partial
x^2}+\frac{\partial^2 \Psi}{\partial y^2}=0$$
Továbbá
$$grad \Phi \cdot grad \psi=\frac{\partial \Phi}{\partial x}\frac{\partial
\Psi}{\partial x}+\frac{\partial \Phi}{\partial y}\frac{\partial \Psi}{\partial
y}=0\;,$$
tehát a $\Phi=const.$ és $\Psi=const.$ vonalak egymásra merőlegesek. $\Phi=
\mathrm{Re} f$ egy lehetséges áramlás sebességpotenciálja,
$\Psi= \mathrm{Im} f$ az ún. áramlási függvény. Szintvonalai merőlegesek $\Phi$
szintvonalaira, azaz áramvonalak. Tehát $$\Psi=konst.$$
az áramvonalak egyenlete.
$w=f(z)$ az áramlás komplex potenciálja.
Komplex sebesség:
$$\frac{dw}{dz}=\frac{df}{dz}=\frac{\partial \Phi}{\partial x}+i\frac{\partial \Psi}{\partial
x}=\underbrace{\frac{\partial \Phi}{\partial x}}_{v_x}-i\underbrace{\frac{\partial \Phi}{\partial
y}}_{v_y}=v_x-iv_y$$
-
Példák:
-
$
\begin{eqnarray}
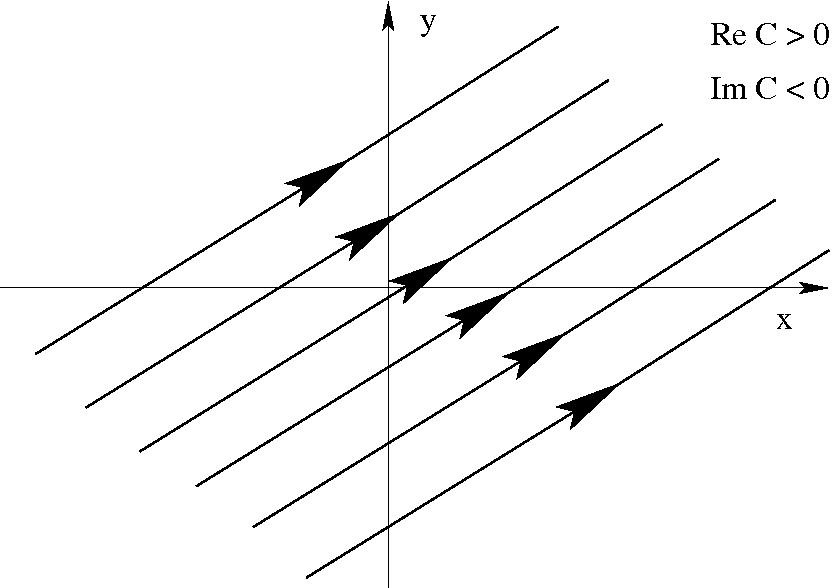
w=C\;z\qquad \qquad \Phi&=&{\rm Re}\; C\; x-{\rm Im}\; C\; y\\
\Psi&=&{\rm Im}\; C\; x+{\rm Re}\; C\; y\\
\frac{dw}{dz}=\;C\;={\rm Re}\; C\;&+&\;i\;{\rm Im}\; C\;
\end{eqnarray}
$
Párhuzamos áramlás
-
$
\begin{eqnarray}
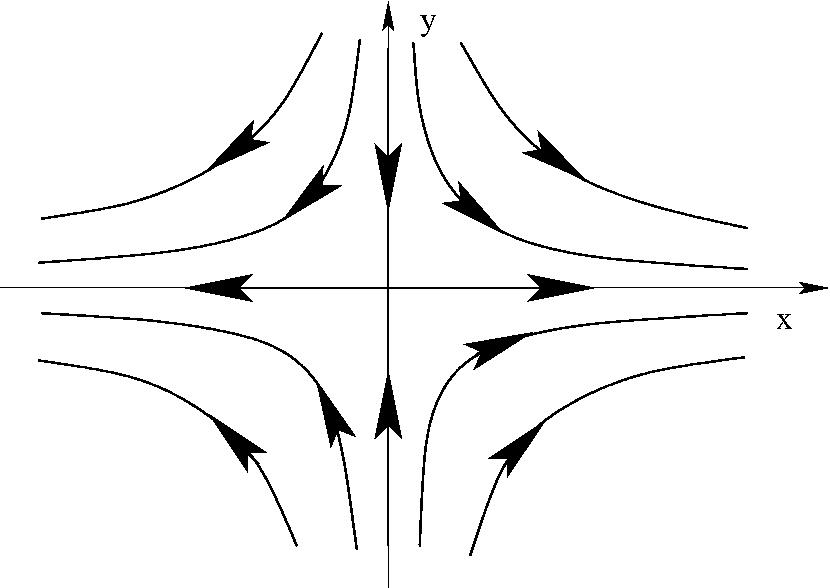
w=C\;z^2\quad (C\;{\rm valós}) \quad \Phi&=&\; C\; (x^2-y^2)\\
\Psi&=&\;2 C\; x\; y\\
\frac{dw}{dz}=\;2C\;z=2C\;(x&+&iy)
\end{eqnarray}
$
Torlódás síknál
Áramlás 90$^\circ$-os sarokban
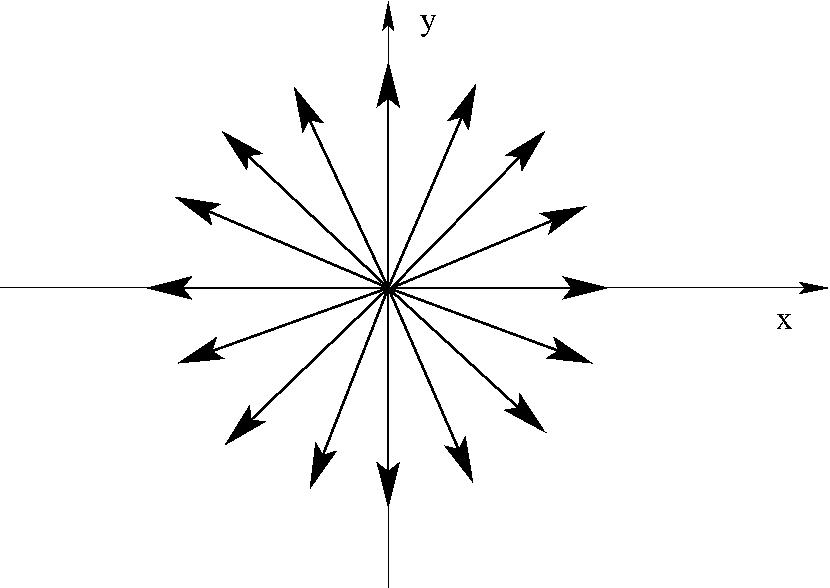
$
\begin{eqnarray}
w=C\;\ln\;z\quad (C\;{\rm valós,\; pozitív}) \quad \Phi&=&\; C\; \ln\;r\\
\Psi&=&\; C\; \varphi\\
\frac{dw}{dz}=\;\frac{C}{z}=\frac{C}{|z|^2}(x&-&iy)
\end{eqnarray}
$
Síkbeli forrás
$
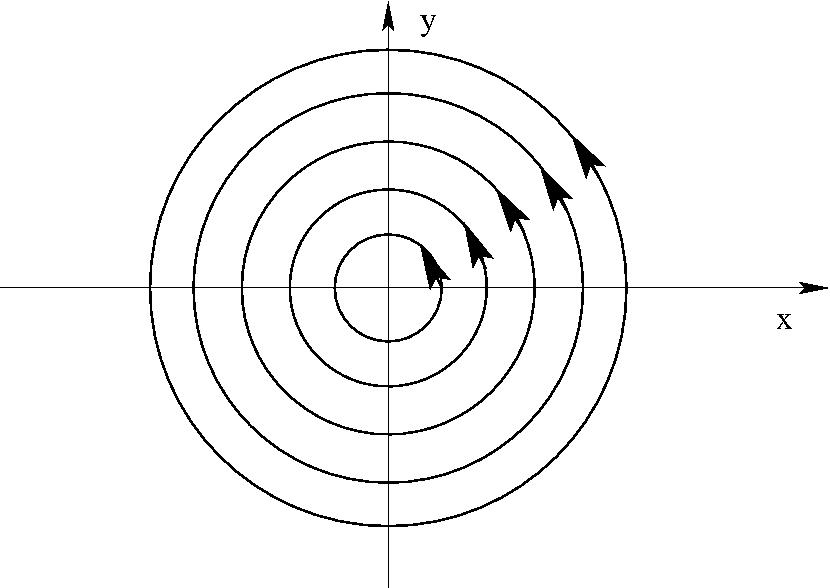
\begin{eqnarray}
w=-iC\;\ln\;z\quad (C\;{\rm valós,\; pozitív}) \quad \Phi&=&\; C\; \varphi\\
\Psi&=&\; -C\;\ln\;r\\
\frac{dw}{dz}=\;\frac{-iC}{z}=\frac{C}{|z|^2}(-y&-&ix)
\end{eqnarray}
$
Síkbeli cirkulációs áramlás
$
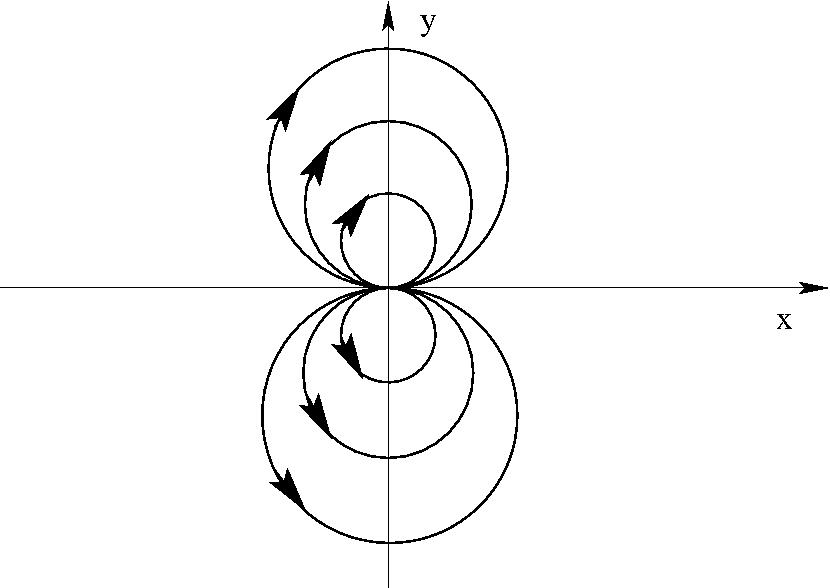
\begin{eqnarray}
w=\frac{C}{z}\quad (C\;{\rm valós}) \quad \Phi&=&\; \frac{C}{r}\; \cos\;\varphi\\
\Psi&=&\; -\frac{C}{r}\; \sin\;\varphi\\
\frac{dw}{dz}=\;-\frac{C}{z^2}=\frac{C}{|z|^2}((y^2-x^2)&+&2ixy)
\end{eqnarray}
$
Dipólus: közeli forrás és nyelő
-
$$w=(C_1+iC_2)\ln\;z$$
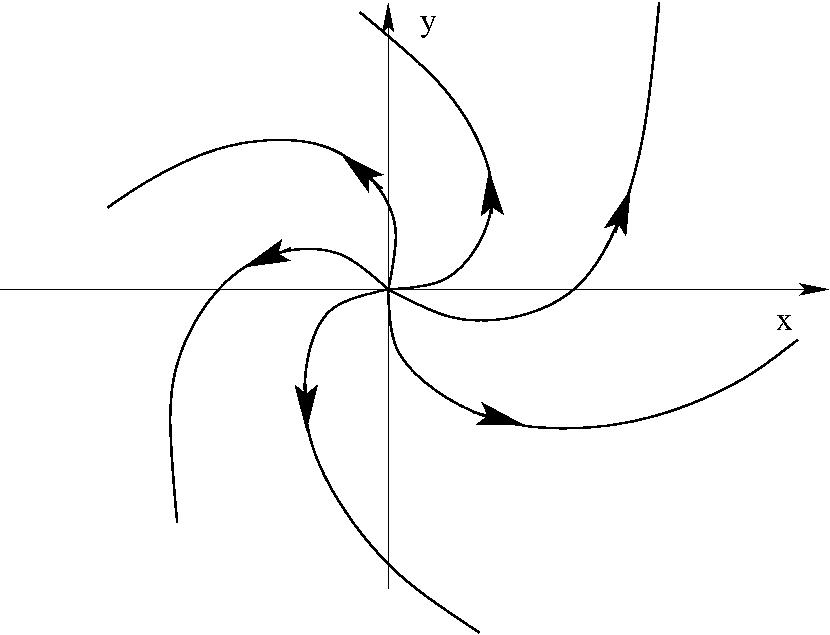
- Henger áramló folyadékban
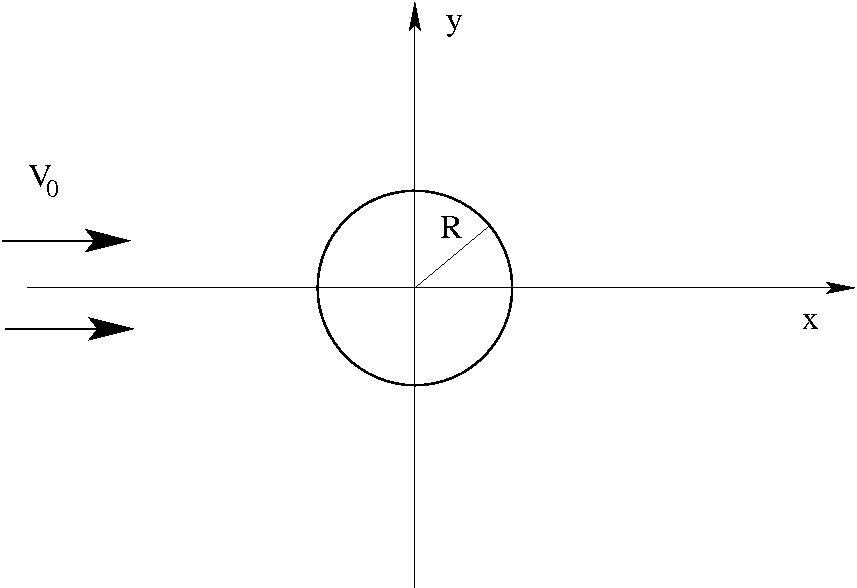
A hengertől nagy távolságban a sebesség $x$ irányú, homogén. Ezért a komplex
sebességben nem szerepelhet $z$ pozitív hatványa (akkor $v_\infty=\infty$
lenne). Így csak konstans és negatív hatványok lehetnek:
$
\begin{eqnarray}
\frac{dw}{dz}&=&v_0+\frac{C_{-1}}{z}+\frac{C_{-2}}{z^2}+\ldots\\
w&=&v_0\;z+C_{-1}\ln z-\frac{C_{-2}}{z}-\frac{C_{-3}}{2z^2}-\ldots\\
z&=&r{\rm e}^{i\varphi}\\
C_{-k}&=&A_k+iB_k
\end{eqnarray}
$
Az áramlási függvény:
$$\Psi={\rm Im}\; w=v_0\;r\sin\varphi +A_1\varphi+B_1\ln
r+\frac{A_2}{r}\sin\varphi-\frac{B_2}{r}\cos\varphi+\frac{A_3}{2r^2}\sin2\varphi$$
Peremfeltétel: $r=R$-re $v_n=0$, azaz a sebesség érintőirányú, tehát
$\left.\Psi\right|_R=konst.$ az $R$ sugarú körön. Ebből következik:
$$A_1=0\;,\quad v_0R+\frac{A_2}{R}=0\;,\quad B_2=0\;,\quad
A_3=A_4=\ldots=0\;,\quad B_3=B_4=\ldots=0\;$$
$$A_2=-v_0R^2\;.\quad {\rm Írjuk,\; hogy}\quad B_1=-\frac{\Gamma}{2\pi}$$
A peremfeltételt kielégítő alak tehát
$$w=v_0z+\frac{v_0R^2}{z}-i\frac{\Gamma}{2\pi}\ln z$$
4.2. Síkbeli áramlások (folytatás)
- Henger áramló folyadékban
A sebességpotenciál:
$$\Phi={\rm Re}\; w=v_0\cos\varphi\left(r+\frac{R^2}{r}\right)+\frac{\Gamma}{2\pi}\varphi$$
Az áramlási függvény:
$$\Psi={\rm Im}\;
w=v_0\sin\varphi\left(r-\frac{R^2}{r}\right)-\frac{\Gamma}{2\pi}\ln r$$
Sebességkomponensek:
$
\begin{eqnarray}
v_r&=&\frac{\partial \Phi}{\partial r}=v_0\cos\varphi\left(1-\frac{R^2}{r^2}\right)\\
v_\varphi&=&\frac{1}{r}\frac{\partial \Phi}{\partial \varphi}=-v_0\sin\varphi\left(1+\frac{R^2}{r^2}\right)+\frac{\Gamma}{2\pi\;r}
\end{eqnarray}
$
A cirkuláció nem redukálható zárt görbén:
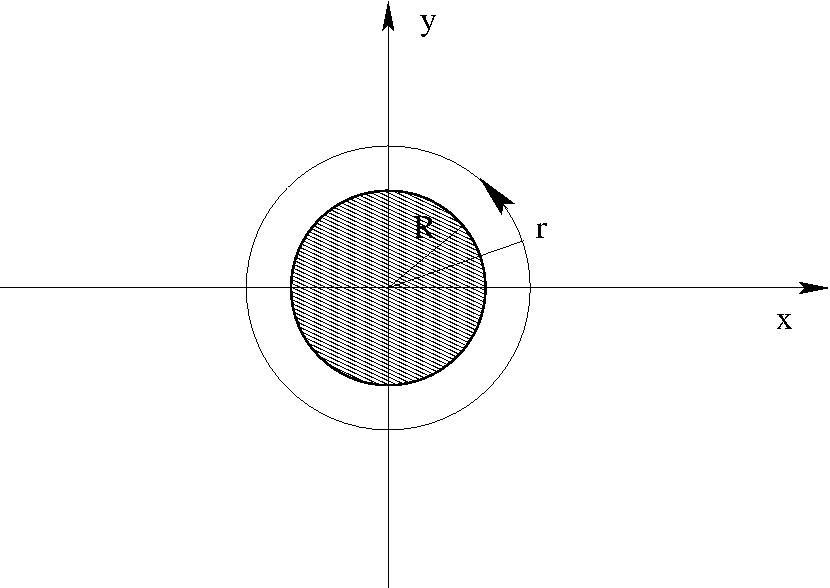
$$\oint {\bf v} d{\bf s}=\int_0^{2\pi}v_\varphi r d\varphi =\Gamma-v_0\left(1+\frac{R^2}{r^2}\right)r\int_0^{2\pi}\sin\varphi \;d\varphi=\Gamma$$
Torlópontok: zérus sebességű pontok.
$$\frac{dw}{dz}=v_0-\frac{v_0R^2}{z^2}-i\frac{\Gamma}{2\pi}\frac{1}{z}=0\quad\Rightarrow\quad
z^2-i\frac{\Gamma}{2\pi}z-R^2=0$$
$$z_\pm=i\frac{\Gamma}{4\pi v_0}\pm \sqrt{R^2-\left(\frac{\Gamma}{4\pi
v_0}\right)^2}$$
Ha $\Gamma=0$:
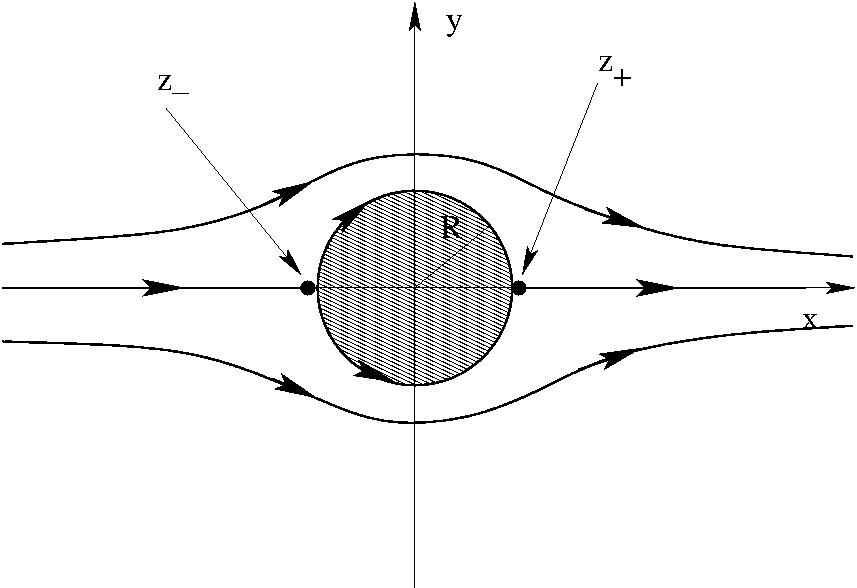
Ha $0 < \Gamma < 4\pi v_0 R$:
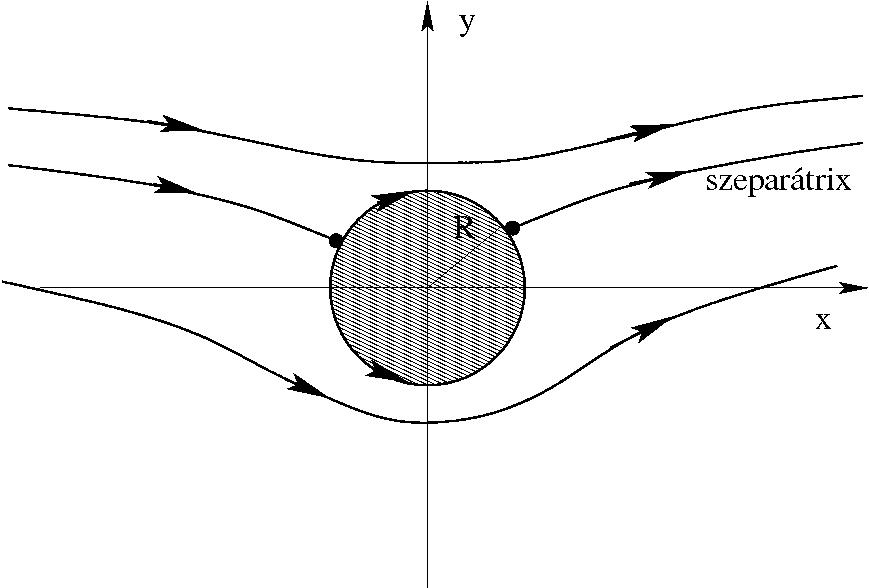
Ha $\Gamma = 4\pi v_0 R$:
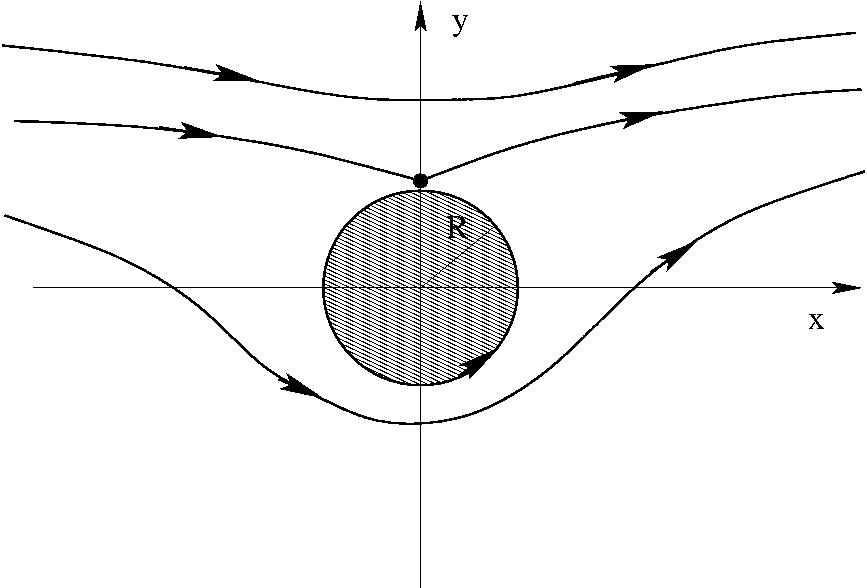
Ha $\Gamma > 4\pi v_0 R$:
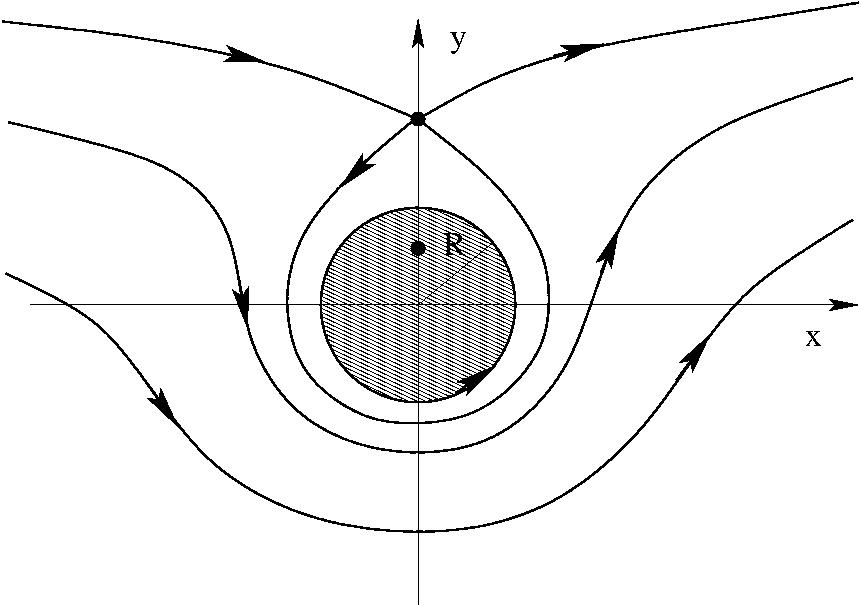
A henger egységnyi hosszára ható erő kiszámítása:
A Bernoulli-egyenletből:
$
\begin{eqnarray}
\frac{1}{2}\rho v^2+p&=&\frac{1}{2}\rho v_0^2+p_0=konst. \quad {\rm
mindenütt}\\
p&=&C-\frac{1}{2}\rho v^2
\end{eqnarray}
$
A henger felületén $v^2=\left(\frac{\Gamma}{2\pi
R}-2v_0\sin\varphi\right)^2$
$${\bf F}=-\oint p{\bf n} ds\;,\quad ds=R\;d\varphi$$
$
\begin{eqnarray}
F_x&=&\frac{1}{2}\rho R\int_0^{2\pi}\left(\frac{\Gamma}{2\pi
R}-2v_0\sin\varphi\right)^2\cos\varphi\; d\varphi-\int_0^{2\pi}C\cos\varphi\;R
d\varphi=0\\
F_y&=&\frac{1}{2}\rho R\int_0^{2\pi}\left(\frac{\Gamma}{2\pi
R}-2v_0\sin\varphi\right)^2\sin\varphi\; d\varphi-\int_0^{2\pi}C\sin\varphi\;R
d\varphi=-\rho v_0 \Gamma
\end{eqnarray}
$
Csak az áramlásra merőleges (felhajtó-) erő hat. A cirkulációt adottnak véve jó
egyezés a tapasztalattal. A cirkulációt a súrlódás hozza létre, amit itt elhanyagoltunk.
- Konform leképezések
Holomorf függvények által létrehozott leképezés: lokálisan nagyító, de
szögtartó és az irányítottságot is tartja (ha $f'(z)\ne 0$).
A komplex potenciál mint leképezés: $w=w(z)$
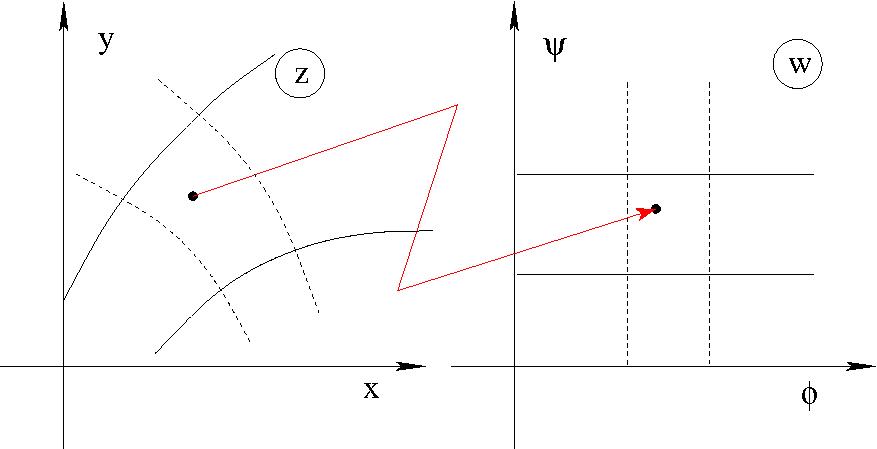
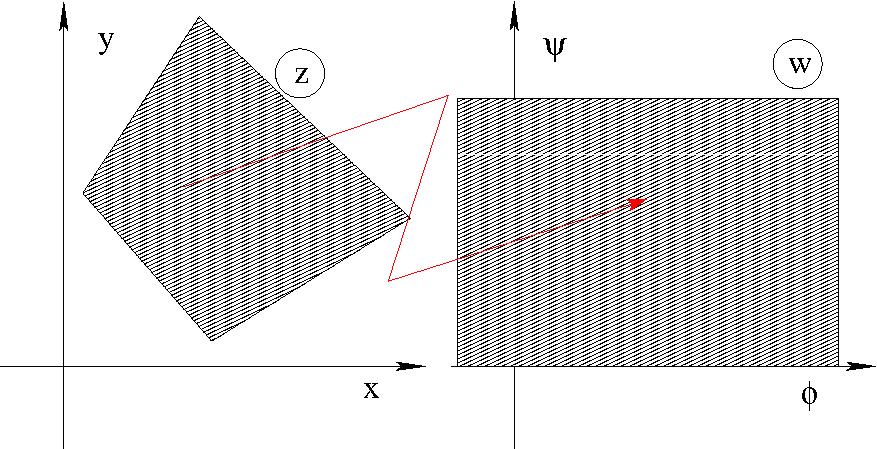
Ahol az áramlást szilárd, mozdulatlan falak határolják, ott a sebesség
tangenciális, tehát a fal valamelyik áramvonallal azonos, ezért ott
$\Psi=const.$ Egyszeresen összefüggő tartomány esetén egyetlen áramvonal fut a
falak mentén, a konstans pedig nullának választható. Ez azt jelenti, hogy a
komplex potenciál az áramlás $(x,y)$ síkban fekvő tartományát a $w$ sík felső
félsíkjába képezi:


 bene@arpad.elte.hu
bene@arpad.elte.hu


 $$\rho f_x \Delta x \Delta y \Delta z -\left(p(x+\Delta
x)-p(x)\right)\Delta y \Delta z=0$$
$$\rho f_x-\frac{\partial p}{\partial x}=0$$
$$\rho f_x \Delta x \Delta y \Delta z -\left(p(x+\Delta
x)-p(x)\right)\Delta y \Delta z=0$$
$$\rho f_x-\frac{\partial p}{\partial x}=0$$
 $$\frac{dp}{dz}=-\rho g = -\frac{Mg}{RT(z)}p$$
$$\frac{dp}{p}= -\frac{Mg}{RT(z)}dz$$
$$\ln \frac{p}{p_0}=-\frac{Mg}{R}\int_{z_0=0}^z\frac{dz'}{T(z')}$$
$$\frac{dp}{dz}=-\rho g = -\frac{Mg}{RT(z)}p$$
$$\frac{dp}{p}= -\frac{Mg}{RT(z)}dz$$
$$\ln \frac{p}{p_0}=-\frac{Mg}{R}\int_{z_0=0}^z\frac{dz'}{T(z')}$$









 Légy
Légy














