Elméleti fizika I.
Bene Gyula
Eötvös Loránd Tudományegyetem, Elméleti Fizikai Tanszék
1117 Budapest, Pázmány Péter sétány 1/A
12. hét pénteki előadás
8.2. Hullámok ideális folyadékban. Hanghullámok
Összenyomható folyadék. Egyensúlyban $\rho_0$, $p_0$ jellemzik (termikus
egyensúly).
Olyan mozgásokat vizsgálunk, melyekre ${\bf f}=0$ és
${\bf v}$, $\rho'=\rho- \rho_0$, $p'=p-p_0$ mindegyike kicsi (kis
rezgés).
$\large
\begin{eqnarray}
\left.\begin{array}{l}
\frac{\partial \rho}{\partial t}+\text{div}(\rho{\bf v})=0\\
\frac{\partial {\bf v}}{\partial
t}+({\bf v}\text{grad}){\bf v}=-\frac{1}{\rho}\text{grad}\;p\\
\frac{\partial s}{\partial t}+({\bf v}\text{grad})s=0
\end{array}\right.\quad\text{kis változások }\Rightarrow
\left.\begin{array}{l}
\frac{\partial \rho'}{\partial t}+\rho_0\text{div}\;{\bf v}=0\\
\frac{\partial {\bf v}}{\partial
t}=-\frac{1}{\rho_0}\text{grad}\;p'\\
\frac{\partial s}{\partial t}=0
\end{array}\right.
\end{eqnarray}
$
Lineáris egyenletek.
Az entrópiasűrűség ($s$) mindenütt állandó, ezért egyértelmű kapcsolat van
$p'$ és $\rho'$ között:
$$p'=\left(\frac{\partial p}{\partial \rho}\right)_s\rho'\quad\quad
\left(\frac{\partial \rho}{\partial
p}\right)_s=-\frac{m}{V^2}\left(\frac{\partial V}{\partial
p}\right)_s=\frac{m}{V}\kappa_s=\rho_0\kappa_s>0$$
Itt $\kappa_s=-\frac{1}{V}\left(\frac{\partial V}{\partial
p}\right)_s
$ az adiabatikus kompresszibilitás.
$\rho'$ és ${\bf v}$ egyenletéből
$
\begin{eqnarray}
\frac{\partial^2 \rho'}{\partial t^2}+\rho_0\text{div}\frac{\partial {\bf v}}{\partial
t}&=&\frac{\partial^2 \rho'}{\partial t^2}-\triangle p'=\frac{\partial^2 \rho'}{\partial t^2}-\left(\frac{\partial p}{\partial \rho}\right)_s\triangle\rho'=0\\
&\Downarrow&\\
\frac{\partial^2 \rho'}{\partial t^2}-c^2\triangle\rho'&=&0\;,\quad c^2=\left(\frac{\partial p}{\partial \rho}\right)_s=\frac{1}{\rho_0\kappa_s}
\end{eqnarray}
$
$0^{\;\circ}$C-on
- levegőben $c=331 \frac{m}{s}$
- vízben $c=1441 \frac{m}{s}$
$
\begin{eqnarray}
\begin{array}{c|c|c|c|c}
&\text{20 Hz}&&\text{16 kHz}&\\
\text{infrahang}&|&\text{hallható hang}&|&\text{ultrahang}
\end{array}
\end{eqnarray}
$
A sűrűség- és nyomásingadozás egyaránt kielégíti a hullámegyenletet.
Az Euler-egyenlet ${\bf v}$ és $p'$-re olyan, mint örvénymentes
áramlásra:
$$\frac{\partial {\bf v}}{\partial
t}=-\frac{1}{\rho_0}\text{grad}\;p'\quad\rightarrow\quad \frac{\partial }{\partial
t}\text{rot}\;{\bf v}=0$$
Mivel kezdetben $\text{rot}\;{\bf v}=0$, később is
$\text{rot}\;{\bf v}=0$.
$${\bf v}=\text{grad}\;\Phi$$
$$\frac{\partial {\bf v}}{\partial
t}+\frac{1}{\rho_0}\text{grad}\;p'=\text{grad}\left(\frac{\partial \Phi}{\partial
t}+\frac{p'}{\rho_0}\right)=0$$
Az integrációs konstanst $\Phi$-be beolvasztva
$$p'=-\rho_0\frac{\partial \Phi}{\partial
t}$$
$$\frac{\partial \rho'}{\partial
t}=\frac{1}{\left(\frac{\partial p}{\partial \rho}\right)_s}\frac{\partial p'}{\partial
t}=-\frac{\rho_0}{c^2}\frac{\partial^2 \Phi}{\partial
t^2}=-\rho_0\text{div}\;{\bf v}=-\rho_0\triangle \Phi$$
$$\frac{\partial^2 \Phi}{\partial
t^2}-c^2\triangle \Phi=0$$
Ebből az következik (az egyenlet gradiensét véve), hogy minden
sebességkomponens is ugyanazt a hullámegyenletet elégíti ki:
$$\frac{\partial^2 {\bf v}}{\partial
t^2}-c^2\triangle {\bf v}=0$$
A hang tehát sűrűség-, nyomás-, sebesség-hullám, sőt, mivel
$T'=T-T_0=\left(\frac{\partial T}{\partial p}\right)_sp'$, hőmérséklet-hullám
is.
Síkhullámok. A $+x$ irányban haladó hullám
$$\Phi=f(x-ct)$$
Itt $f$ tetszőleges egyváltozós függvény.
$$v_x=f'(x-ct)\;,\quad v_y=v_z=0$$
Longitudinális hullám.
$$p'=\rho_0c f'(x-ct)\;,\quad \rho'=\frac{\rho_0}{c} f'(x-ct)\;,\quad
p'=c^2\rho'$$
A linearizálás feltétele: $\frac{v_x}{c}=\frac{\rho'}{\rho_0}\ll 1$.
Monokromatikus síkhullám:
$$\Phi=\text{Re}\left(A\text{e}^{i({\bf k}{\bf r}-\omega
t)}\right)\;,\quad {\bf k}=\frac{\omega}{c}{\bf n}$$
Itt ${\bf n}$ a terjedési irány, $k=\frac{2\pi}{\lambda}$ a hullámszám,
$\lambda$ a hullámhossz, $\omega=2\pi \nu$ a körfrekvencia, $\nu$ a frekvencia.
$$c=\nu\lambda\;,\quad \omega=kc$$
Ezek az összefüggések csak nyugvó közegben érvényesek.
8.3. Hangterjedés mozgó közegben
K koordinátarendszer: homogén folyadékáramlás ${\bf u}$ sebességgel.
K' koordinátarendszer: a folyadék nyugalomban van
$${\bf r}={\bf u}t+{\bf r}'$$
Zavar: a közeget az egyensúlyból kimozdító fizikai hatás, pl. nyomásváltozás.
-
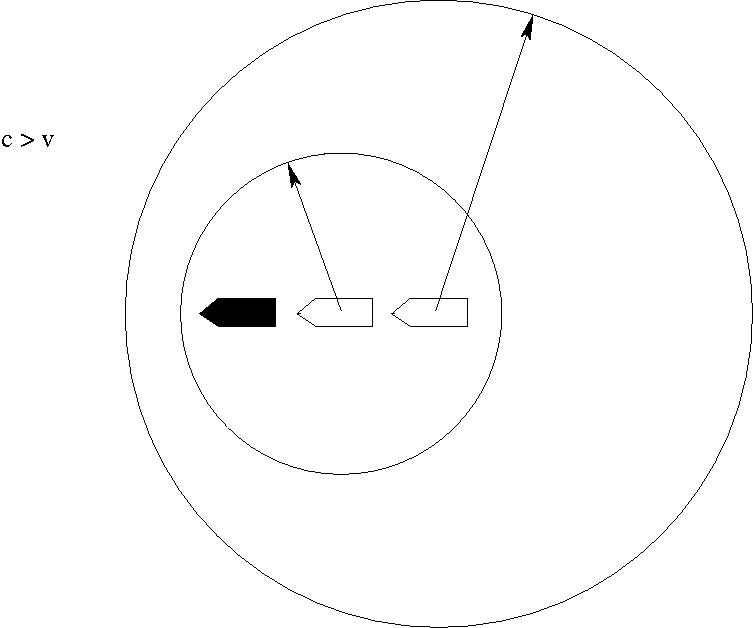
A K' rendszerben a zavar minden irányban $c$ sebességgel terjed. A K
rendszerben a zavar terjedési sebessége ${\bf n}$ irányban
$${\bf u}+c{\bf n}$$
Az áramlás elsodorja a zavart.
-
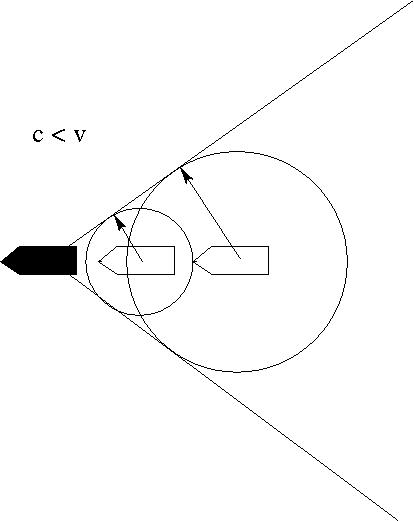
Az O pontban keltett zavar által elérhető tartomány egységnyi idő alatt:
$u< c$: Gömb belseje
$u> c$: $2\alpha$ nyílásszögű kúp belseje, ahol $\sin \alpha=\frac{c}{u}$ a Mach-szám.
-
Doppler-jelenség:
A K'rendszerben:
$$\Phi=A\text{e}^{i({\bf k}{\bf r}'-\omega'
t)}\;,\;\omega'=ck$$
A K rendszerben:
$${\bf r}'={\bf r}-{\bf u}t\;,\quad \Phi=A\text{e}^{i({\bf k}{\bf r}'-\omega'
t)}=A\text{e}^{i({\bf k}{\bf r}-(\omega'+{\bf k}{\bf u})
t)}\;,\;\omega=\omega'+{\bf k}{\bf u}=\omega'\left(1+\frac{{\bf u}{\bf n}}{c}\right)=\omega'\left(1+\frac{u}{c}\cos\theta\right)$$
A felénk fújt hang magasabb ($\cos\theta=1$), a tőlünk fújt hang mélyebb ($\cos\theta=-1$).
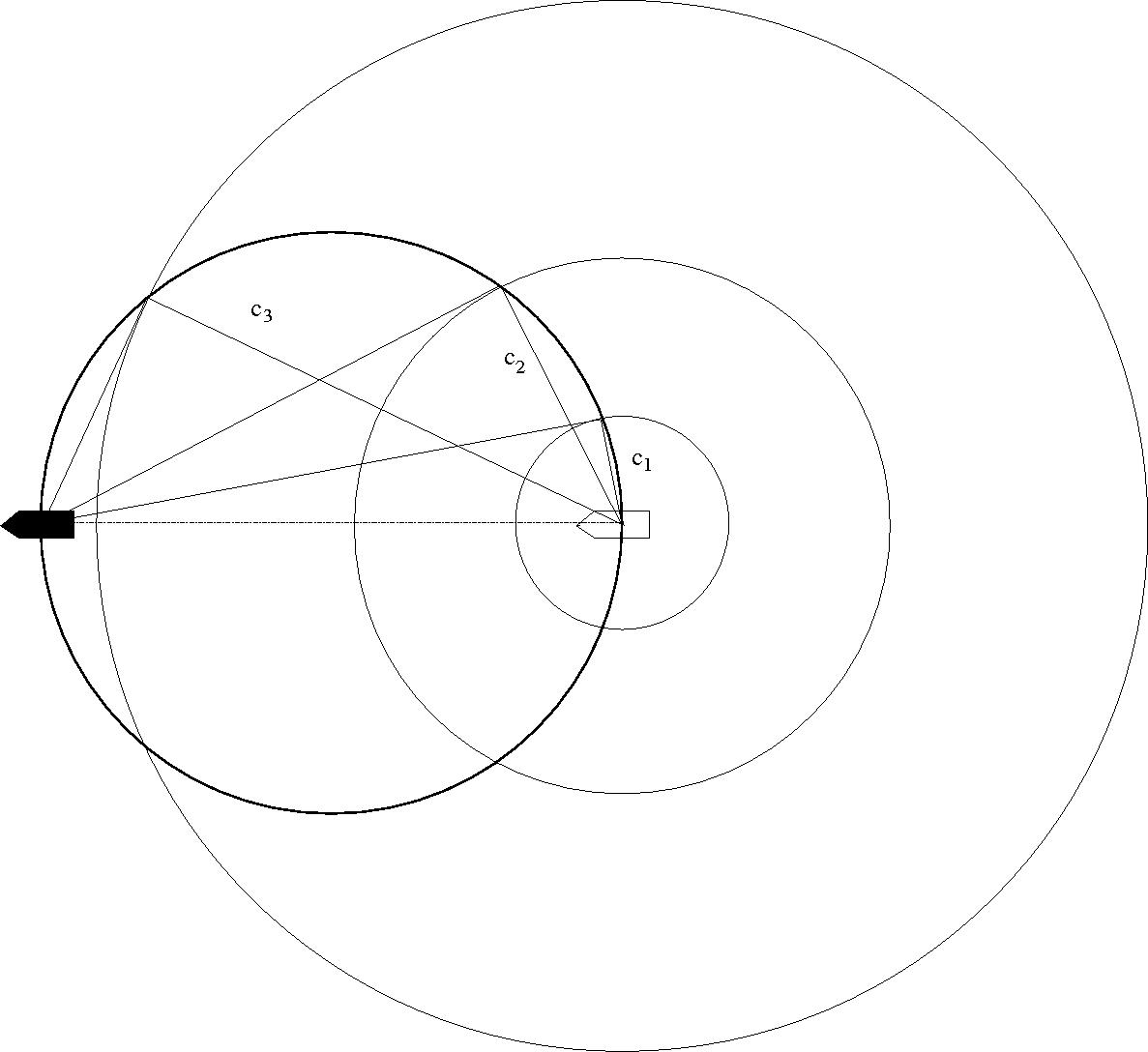
8.4. Mozgó hangforrás nyugvó közegben
A forrás ${\bf u}$ sebességgel mozog.
A kibocsátott hang által elért tartomány szuperszónikus mozgás esetén
$2\alpha$ nyílásszögű kúp belseje.
A forrással együttmozgó K' rendszerben a folyadék $-{\bf u}$ sebességgel
mozog. A frekvencia itt $\omega_0$. Az álló K rendszerben izotróp a
hangterjedés (mivel a folyadék nyugalomban van), de nem $\omega_0$ a
frekvencia.
A K'rendszerben:
$$\Phi=A\text{e}^{i({\bf k}{\bf r}'-\omega_0
t)}$$
A K rendszerben:
$${\bf r}'={\bf r}-{\bf u}t\;,\quad \Phi=A\text{e}^{i({\bf k}{\bf r}'-\omega_0
t)}=A\text{e}^{i({\bf k}{\bf r}-(\omega_0+{\bf k}{\bf u})
t)}=A\text{e}^{i({\bf k}{\bf r}-\omega t)}\;,\quad \omega=ck$$
$$\omega=\omega_0+{\bf k}{\bf u}=\omega_0+\omega\frac{{\bf u}{\bf n}}{c}\quad\Rightarrow\quad
\omega=\frac{\omega_0}{1-\frac{u}{c}\cos\theta}$$
A közeledő hangforrás magasabb, a távolodó alacsonyabb hangot ad.
8.5. Mikor tekinthető összenyomhatatlannak egy áramlás?
${\bf f}=0$. Bernoulli-egyenlet:
$$\frac{v^2}{2}+\int_{p_0}^p\frac{dp}{\rho(p)}=0$$
Ha a folyadék kissé összenyomható,
$$\rho(p)\approx
\underbrace{\rho(p_0)}_{\rho_0}+\underbrace{\left(\frac{\partial\rho}{\partial
p}\right)_s}_{\rho_0\kappa_s}(p-p_0)=\rho_0\left(1+\kappa_s(p-p_0)\right)$$
$$\frac{1}{\rho(p)}=\frac{1}{\rho_0}\left(1-\kappa_s(p-p_0)\right)$$
$$\Downarrow$$
$$\frac{v^2}{2}+\frac{1}{\rho_0}(p-p_0)-\frac{1}{2}\frac{\kappa_s}{\rho_0}(p-p_0)^2=0$$
Ha az utolsó tag elhanyagolható, akkor tekinthető összenyomhatatlannak a
folyadék:
$$\frac{1}{2}\frac{\kappa_s}{\rho_0}(p-p_0)^2\ll \frac{v^2}{2}$$
Mivel ilyenkor $p-p_0\approx -\frac{\rho_0}{2}v^2$, ezzel az
összenyomhatatlanság feltétele
$$\frac{1}{8}\kappa_s\rho_0 v^4\ll \frac{v^2}{2}$$
azaz, mivel $\kappa_s\rho_0 =1/c^2$,
$$\frac{1}{8}\frac{v^4}{c^2}\ll \frac{v^2}{2}$$
vagy
$$\frac{1}{4}\frac{v^2}{c^2}\ll 1$$
8.6. Hangkeltés. Hangterjedés, visszaverődés és törés.
-
Hangkeltés
Az elektrodinamikából ismeretes, hogy a hullámegyenlet megoldása a forrástól nagy távolságban
$$\Phi({\bf r},t)=\text{div}\frac{{\bf P}\left(t-\frac{r}{c}\right)}{r}$$
alakú, ahol ${\bf P}(t)$ a forrásra jellemző mennyiség (a dipólnyomaték). A $c\rightarrow\infty$ határeset az összenyomhatatlan folyadéknak felel meg, ezért ${\bf P}(t)$ az a mennyiség, amely ilyenkor megjelenik a forrásként szereplő test körüli áramlást leíró sebességpotenciálban nagy $r$-re. $\Phi({\bf r},t)$ ilyenkor mindig $\text{div}{\bf P}(t)/r$ alakú, hacsak a test nem pulzál. ${\bf P}$ a test sebességével lesz arányos, gömbre pl. ${\bf P}(t)=\frac{1}{2}R^3{\bf v}_0(t)$. A hullámzónában ($r\gg \lambda$) elég a számlálót deriválni (egyéb tagok $1/r$-nél gyorsabban tartanak nullához), így
$\begin{eqnarray}
\Phi( {\bf r} ,t)=-\frac{\dot{{\bf P}} \left(t-\frac{r}{c}\right) {\bf n} }{cr}
\end{eqnarray}$
és
$${\bf v}=\text{grad}\; \Phi=\frac{\ddot{ {\bf P}}\left(t-\frac{r}{c}\right){\bf n}}{c^2r}{\bf n}$$
Energiaáram-sűrűség: $cE{\bf n}$, ahol síkhullámra $E=\rho_0v^2$.
A kisugárzott intenzitás
$$I=\int c\rho_0\underbrace{\overline{v^2}}_{\text{időátlag}}{\bf n}d{\bf F}\underbrace{=}_{\text{gömbre}}\frac{2\pi\rho_0}{c^3}\overline{\ddot P^2}\int_0^\pi \cos^2\vartheta\sin\vartheta d\vartheta=\frac{4\pi\rho_0}{3c^3}\overline{\ddot P^2}$$
Mivel $P\propto v_0$, harmonikus rezgés esetén $I\propto\omega^4$.
Gömbre pl.
$$I=\frac{\pi\rho_0 R^6}{3c^3}v_0^2\omega^4$$
Henger esetén (a henger egységnyi hosszára vonatkoztatva)
$$I=\frac{\pi^2\rho_0 R^4}{4c^2}v_0^2\omega^3$$
-
Hangterjedés
- A hőmérséklet, és ezzel együtt $c$ felfelé növekszik:
Teljes visszaverődés, nagy távolságban hallani a hangot.
- A hőmérséklet, és ezzel együtt $c$ felfelé csökken:
A hang nem hallható.
- A magas hangok messziről nem hallhatók (erősebb a csillapodásuk).
-
Visszaverődés és törés
$$\vartheta=\vartheta'$$
$$\frac{\sin\vartheta''}{\sin\vartheta}=\frac{c_2}{c_1}$$
$\vartheta$ : beesési szög, $\vartheta'$ : visszaverődési szög, $\vartheta''$ : törési szög.
-
Szórás
Kis test által szórt hang teljes szórási hatáskeresztmetszete a hang frekvenciájának negyedik hatványával arányos.
9.1. Az egydimenziós hullámegyenlet D'Alembert-féle
megoldása
$$\frac{\partial^2 \Phi}{\partial
t^2}-c^2\frac{\partial^2 \Phi}{\partial
x^2}=0$$
Az általános megoldás (végtelen közeg esetén)
$$\Phi(x,t)=a(x-ct)+b(x+ct)$$
alakú. Olyan megoldást keresünk, amely kielégíti a
$$\Phi(x,0)=f(x)$$ és
$$\left.\frac{\partial \Phi(x,t)}{\partial t}\right|_{t=0}=g(x)$$
kezdeti feltételeket. Az általános megoldást beírva
$\begin{eqnarray}
a(x)+b(x)&=& f(x)\\
-c\;a'(x)+c\;b'(x)&=& g(x)
\end{eqnarray}$
A második egyenletet integrálva:
$$b(x)-a(x)=\frac{1}{c}\int_{x_0}^x g(\xi)d\xi$$
Itt a tetszőleges $x_0$ felel meg az integrációs konstansnak.
Ezután
$$a(x)=\frac{1}{2}f(x)-\frac{1}{2c}\int_{x_0}^x g(\xi)d\xi$$
és
$$b(x)=\frac{1}{2}f(x)+\frac{1}{2c}\int_{x_0}^x g(\xi)d\xi$$
Ezzel a keresett megoldás:
$$\Phi(x,t)=\frac{1}{2}\left(f(x-ct)+f(x+ct)\right)+\frac{1}{2c}\int_{x-ct}^{x+ct} g(\xi)d\xi$$
9.2. Sajátrezgések, állóhullámok.
Külső erő hatása nélkül végbemenő szabad rezgések véges edényben. A határfeltételek miatt frekvenciájuk nem tetszőleges $\rightarrow$ sajátrezgések (végtelen sok módus lehetséges)
Állóhullámok alakulnak ki
$$\Phi=\Phi_0({\bf r})\cos \omega t\;,$$
ahol
$$\triangle \Phi_0+\frac{\omega^2}{c^2}\Phi_0=0\quad \text{+ határfeltételek}$$
A határfeltételek meghatározzák $\omega$-t is. A megoldások szuperpozíciója is megoldás (linearitás).
- Sípok.
- Vékony, zárt cső (zárt nyelvsíp)
A cső hossza legyen $L$, vastagsága elhanyagolható.
$$\left.v_x\right|_{x=0}=\frac{\partial \Phi_0}{\partial x}=0\quad\quad\quad
\left.v_x\right|_{x=L}=\frac{\partial \Phi_0}{\partial x}=0$$
$$\Phi_0''(x)=-\frac{\omega^2}{c^2}\Phi_0(x)\quad\rightarrow\quad
\Phi_0(x)=A\cos\left(\frac{\omega}{c}x\right)+B\sin\left(\frac{\omega}{c}x\right)$$
$$\Phi_0'(0)=0\;\rightarrow \;B=0\quad\quad\quad \Phi_0'(0)=0=-A\frac{\omega}{c}\sin\left(\frac{\omega}{c}x\right)$$
$$\Downarrow$$
$$\Phi_0(x)=A\cos\left(\frac{\omega_n}{c}x\right)\quad\quad\quad \frac{\omega_n}{c}L=\pi n\;n=1,2,\ldots$$
Sajátfrekvencia:
$$\omega_n=\pi\frac{c}{L}n\quad\nu_n=\frac{c}{2L}n\quad \lambda_n=\frac{c}{\nu_n}$$
$$v_x(x)=-\underbrace{A\frac{\pi}{L}n}_{v_{x max}}\sin\left(\frac{\pi}{L}nx\right)\cos \omega_n t$$
$$p'(x)=-\rho_0\frac{\partial \Phi}{\partial t}=\rho_0\omega_n A\cos\left(\frac{\pi}{L}nx\right)\sin \omega_n t$$
Ahol $v_x$ maximális, ott $p$ minimális (v.ö. Bernoulli-tétel), ellentétes rezgés.
$$p'(x)\propto \rho'(x)$$
Ugyanilyen képletek érvényesek a megfeszített húr rezgéseire. Ott a rezgés transzverzális, tehát $z \ne 0$ és $c=\sqrt{\frac{\sigma}{\rho}}$.
ezzel a kezdeti kitéréssel
$$z=A_1\sin\left(\frac{\pi}{L}x\right)\cos\left(\pi\frac{c}{L}t\right)+
A_2\sin\left(2\frac{\pi}{L}x\right)\cos\left(2\pi\frac{c}{L}t\right)$$
Csak az alaphang és oktávja szólal meg.
Minden felhang megszólal (különböző intenzitással).
A zárt cső mint rezonátor előfordul az orgona nyelvsípjai között.

A kialakuló hullámok
| $n=1$ | $\nu_1=\frac{c}{2L}$ | alaphang ($c^1$)
|
|---|
| $n=2$ | $\nu_2=\frac{c}{L}$ | oktáv ($c^2$)
|
|---|
| $n=3$ | $\nu_3=\frac{3}{2}\frac{c}{L}$ | (tiszta) kvint 3:2 ($g^2$)
|
|---|
| $n=4$ | $\nu_4=2\frac{c}{L}$ | oktáv ($c^3$)
|
|---|
| $n=5$ | $\nu_5=\frac{5}{2}\frac{c}{L}$ | (nagy) terc 5:4 ($e^3$)
|
|---|
| $n=6$ | $\nu_6=3\frac{c}{L}$ | kvint 3:2 ($g^3$)
|
|---|
| $n=7$ | $\nu_7=\frac{7}{2}\frac{c}{L}$ | kis szeptim 7:4 ($b^3$)
|
|---|
| $n=8$ | $\nu_8=4\frac{c}{L}$ | oktáv ($c^4$)
|
|---|
Az általános megoldás
$$v_x(x,t)=\sum_{n=1}^\infty A_n\sin\left(\frac{\pi}{L}n x\right)\cos\left(\pi\frac{c}{L}n t\right)$$
Fourier-sor. Az $A_n$ együtthatókat a kezdeti feltételek határozzák meg.
A hangszínt az amplitudó-eloszlás $\{A_n\}$ adja meg. (Pl.: üveghang, ha a páratlan felharmonikusokat kizárjuk.)
- Nyitott nyelvsíp
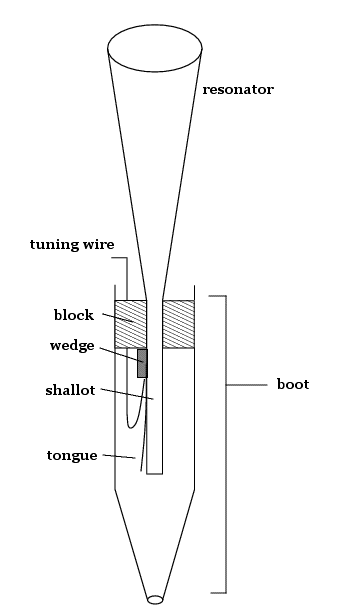
A tetején ($x=L$) $p=$áll., tehát $p'$ csomópontja, azaz $v_x$ maximuma. Az alaphang ezért $\lambda_1=4L$ hullámhosszú, $\nu_1=\frac{c}{4L}$ frekvenciájú (mélyebb, mint a zártnál).
A következő felhang csak $\lambda_2=\frac{4}{3}L$ hullámhosszú lehet, $\nu_2=\frac{3}{4}\frac{c}{L}$, tehát csak a páratlan felhangok jelennek meg.
$$\nu_{n'}=\frac{c}{4L}n'\;,\;n'=1,3,5,\ldots$$
- Ajaksípok

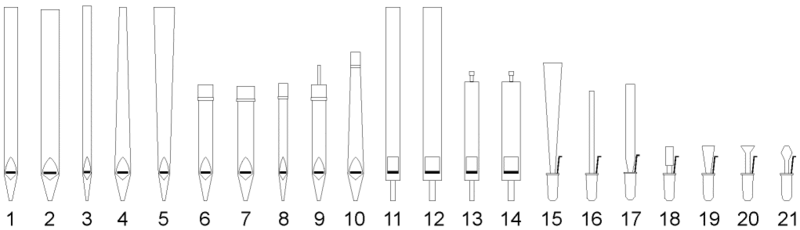
Erősen fújva alul maximális a sebesség (pl. orgona).
Nyitott eset:
$$\nu_n=\frac{c}{2L}n\;,\;n=1,2,3,\ldots$$
Zárt eset:
$$\nu_{n'}=\frac{c}{4L}n'\;,\;n'=1,3,5,\ldots$$
Blockflöte gyengén fújva, mint nyelvsíp:
alaphangja: $\nu=\frac{c}{4L}\approx \frac{330}{4\cdot 0.3}=225 Hz$ (valójában $c^1=264 Hz$)
Erősen fújva, mint ajaksíp. Az alt (f) és szoprán blockflöte csövének hosszaránya $\approx 1.5$.
- Téglatest sajátrezgései.
$v_n=0$ a falakon.
Egyetlen állóhullám:
$$\Phi({\bf r},t)=A\cos\left(\frac{\pi}{L_1}lx\right)\cos\left(\frac{\pi}{L_2}my\right)\cos\left(\frac{\pi}{L_3}nz\right)$$
$$\Downarrow$$
$$\omega^2=c^2\pi^2\left(\frac{l^2}{L_1^2}+\frac{m^2}{L_2^2}+\frac{n^2}{L_3^2}\right)$$
$l,m,n$ egész számok. Mindegyik számhármas meghatároz egy sajátfrekvenciát. Ezek sorozata sokkal bonyolultabb, mint a felhangoké.
Egy általános rezonátordobozbeli megoldás
$$\Phi({\bf r},t)=\sum_{i=1}^\infty A_i \Phi_{i0}({\bf r})\cos(\omega_i t+\alpha_i)$$
Itt $\alpha_i$-k az egyes rezgési módusok kezdeti fázisai.
$\omega_i$ diszkrét, de szabálytalan értékeket vehet fel.
A hangszer hangszíne a rezonátorban kialakuló sajátrezgésektől és azok amplitudóeloszlásától $\{A_i\}$ függ.
Rezonátor: hegedűtest, cső.
9.4. Nehézségi hullámok (vízhullámok).

Véges mélységű folyadékban
Feltesszük, hogy $y$-tól nem függ semmi (széles medence)
Összenyomhatatlan folyadékot vizsgálunk
Feltesszük, hogy az áramlás örvénymentes: ${\bf v}=\text{grad}\;\Phi$
Alapegyenletek:
$$\triangle \Phi=0$$
$$\frac{\partial \Phi}{\partial t}+\frac{1}{2}\left(\text{grad}\;\Phi\right)^2+\frac{p-p_0}{\rho_0}+gz=0$$
Bernoulli-egyenlet, $p_0$ az atmoszférikus nyomás.
Peremfeltételek:
A felület egyenlete $z=\zeta(x,t)$
- A felületi sebesség $\zeta$ változásából adódik
Egy részecske sebessége közvetlenül a felület alatt
$$\dot z=\frac{d\zeta}{dt}=\frac{\partial \zeta}{\partial t}+v_x\frac{\partial \zeta}{\partial x}$$
$$\Downarrow$$
$$\left.\frac{\partial \Phi}{\partial z}\right|_\zeta=\frac{\partial \zeta}{\partial t}+v_x\frac{\partial \zeta}{\partial x}$$
- A nyomás $\zeta$-nál $p_0$:
$$\left.\left(\frac{\partial \Phi}{\partial t}+\frac{1}{2}\left(\text{grad}\;\Phi\right)^2+gz\right)\right|_\zeta=0$$
- Alul nincs $z$ irányú sebesség:
$$\left.\frac{\partial \Phi}{\partial z}\right|_{z=-h}=0$$
9.5. Lineáris vízhullámok.
Ha $v$ és $\zeta$ kicsi, akkor a négyzetes tagok a lineárisak mellett elhagyhatók:
Egyenletek:
$$\triangle \Phi=0$$
$$\frac{\partial \Phi}{\partial t}+\frac{p-p_0}{\rho_0}+gz=0$$
Peremfeltételek:
- $$\left.\frac{\partial \Phi}{\partial z}\right|_\zeta=\frac{\partial \zeta}{\partial t}=\dot z$$
-
$$\left.\left(\frac{\partial \Phi}{\partial t}+gz\right)\right|_\zeta=0$$
- A fenti két peremfeltételből következik, hogy
$$\left.\left(\frac{\partial^2 \Phi}{\partial t^2}+g\frac{\partial \Phi}{\partial z}\right)\right|_\zeta=0$$
-
$$\left.\frac{\partial \Phi}{\partial z}\right|_{z=-h}=0$$
pozitív irányba haladó hullámot keresünk. Feltevés:
$$\Phi(x,z,t)=\Phi_0(x-ct)\chi(z)$$
$$\triangle \Phi=0\quad\Rightarrow\quad \Phi_0''\chi+\Phi_0\chi''=0$$
$$\frac{\Phi_0''}{\Phi_0}=-\frac{\chi''}{\chi}$$
A baloldal csak $x-ct$-től, a jobboldal csak $z$-től függ, ezért mindkettő konstans kell hogy legyen:
$$\Phi_0''=-k^2\Phi_0\quad\quad\quad\chi''=k^2\chi$$
$c$ függhet $k$-tól!
Megoldás:
$$\Phi_0(x-ct)=A_1\cos(kx-\underbrace{kc(k)}_{\equiv \omega(k)}t)\;,\quad \chi(z)=A\;\text{ch}k(z+h)+B\;\text{sh}k(z+h)$$
$k$ a hullámszám.
Az utolsó peremfeltétel miatt $B=0$.
Tehát
$$\Phi(x,z,t)=A\cos(kx-kct)\;\text{ch}k(z+h)$$
Az utolsóelőtti peremfeltételből
$$\omega^2 A\;\text{ch}k(\zeta +h)=gkA\;\text{sh}k(\zeta +h)$$
Mivel $\zeta\ll h$ gyenge zavar esetén,
$$\omega^2=gk\;\text{th}kh$$
azaz
$$\omega=\sqrt{gk\;\text{th}kh}$$
A körfrekvencia és a hullámszám között nemlineáris a kapcsolat $\rightarrow$ diszperzió: a terjedési sebesség függ a hullámhossztól.
A második határfeltételből a hullámfelület:
$$\zeta(x,t)=\left.-\frac{1}{g}\frac{\partial \Phi}{\partial t}\right|_{\zeta\approx 0}=\frac{A\omega}{g}\;\text{ch}kh \sin(kx-\omega t)$$
A diszperzió következményei
- Fázissebesség és csoportsebesség
Fázissebesség:
$$c=\frac{\omega(k)}{k}$$
Csoportsebesség:
$$c_g=\frac{d \omega(k)}{d k}$$
A csoportsebesség jelentése:
$$\zeta(x,t)=\int dk f(k) {\rm e}^{i(kx-\omega(k)t)}$$
A hullámhegyek és hullámvölgyek azok a helyek, ahol az interferencia erős,
vagyis a fázis csak lassan változik a hullámszám függvényében. Ennek feltétele:
$$\frac{\partial}{\partial k}\left(kx-\omega(k)t\right)=0$$
azaz
$$x=\frac{d \omega(k)}{d k}t$$
A hullámhegyek és hullámvölgyek tehát a csoportsebességgel mozognak.
Lineáris vízhullámok esetén a fázissebesség
$$c=\sqrt{\frac{g}{k}\;\text{th}kh}\;,$$
a csoportsebesség
$$c_g=\frac{1}{2}\sqrt{\frac{g}{k}\;\text{th}kh}+\frac{h}{2}\sqrt{\frac{g
k }{\text{sh}kh\;\text{ch}^3 kh}}=\frac{1}{4}\sqrt{\frac{g\left(\text{sh}^2(2kh)+(2kh)^2\right)}{k\;\text{sh}kh\;\text{ch}^3 kh}}\;.$$
Határesetek:
- mély víz:
$$\lambda=\frac{2\pi}{k}\ll h\quad \rightarrow \quad kh\gg 1\;,\quad
\text{th}kh\approx 1$$
$$\omega(k)=\sqrt{gk}$$
Fázissebesség:
$$c=\sqrt{\frac{g}{k}}$$
Csoportsebesség:
$$c_g=\frac{1}{2}\sqrt{\frac{g}{k}}=\frac{c}{2}$$
- sekély víz:
$$\lambda=\frac{2\pi}{k}\gg h\quad \rightarrow \quad kh\ll 1\;,\quad
\text{th}kh\approx kh$$
$$\omega(k)=\sqrt{gh}k$$
Nincs diszperzió, a fázissebesség egyenlő a csoportsebességgel:
$$c=c_g=\sqrt{gh}$$
- Szétfolyás
Legyen a kezdeti hullámalak $\sigma$ félszélességű haranggörbe (Gauss-függvény):
$$\zeta(x,0)=A\exp\left(-\frac{x^2}{2\sigma^2}\right)=\text{Re }\frac{A\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty
{\rm e}^{-\frac{\sigma^2}{2}k^2}{\rm e}^{ikx}dk$$
Ekkor
$$\zeta(x,t)=\text{Re }\frac{A\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty
{\rm e}^{-\frac{\sigma^2}{2}k^2}{\rm e}^{i(kx-\omega(k)t)}dk$$
Ha
$$\omega(k)\approx
\left.\frac{d\omega(k)}{dk}\right|_{k=0}k+\frac{1}{2}\left.\frac{d^2\omega(k)}{dk^2}\right|_{k=0}k^2=ak+\frac{1}{2}bk^2\;,$$
akkor
$$\zeta(x,t)=\text{Re }\frac{A\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty
{\rm e}^{-\frac{\sigma^2+ibt}{2}k^2}{\rm e}^{ik(x-at)}dk=\text{Re }A\sqrt{\frac{\sigma^2}{\sigma^2+ibt}}\exp\left(-\frac{(x-at)^2}{2(\sigma^2+ibt)}\right)=A\sqrt[4]{\frac{\sigma^4}{\sigma^4+b^2t^2}}\exp\left(-\frac{(x-at)^2}{2(\sigma^2+b^2t^2/\sigma^2)}\right)\cos\left(\frac{(x-at)^2bt}{2(\sigma^4+b^2t^2)}+\delta\right)$$
Ennek burkolója $\sqrt{\sigma^2+b^2t^2/\sigma^2}>\sigma$ félszélességű haranggörbe (melynek maximuma
az $x=at$ helyen van).
A szétfolyás oka: az egyes monokromatikus összetevők
különböző sebességgel haladnak, így az idő múlásával egyre
inkább rendezetlen fázisokkal adódnak össze. $\rightarrow$ Az amplitudó csökken,
a szélesség növekszik.
- Hullámtörés

$\lambda > h$ esetén $c=\sqrt{gh}$, ezért a mélyebb vízben terjedő hullámok
gyorsabbak, utolérik a sekélyebb vízben terjedőket és átbuknak rajtuk.

Cunami (szökőár), 2004, Thaiföld. A tengerrengés okozta hullámok a
nyílt óceánon többszáz kilométer hullámhosszúságúak és mindössze kb. 300mm-es
amplitudójúak. Partközelben lelassulnak, feltorlódnak (4-30 méteres magasságú vízfallá), és az addig nagy
területen szétoszló energiájuk a partszakaszokon koncentrálódva hatalmas
pusztítást okoz.
- Kelvin-féle hajóhullámok
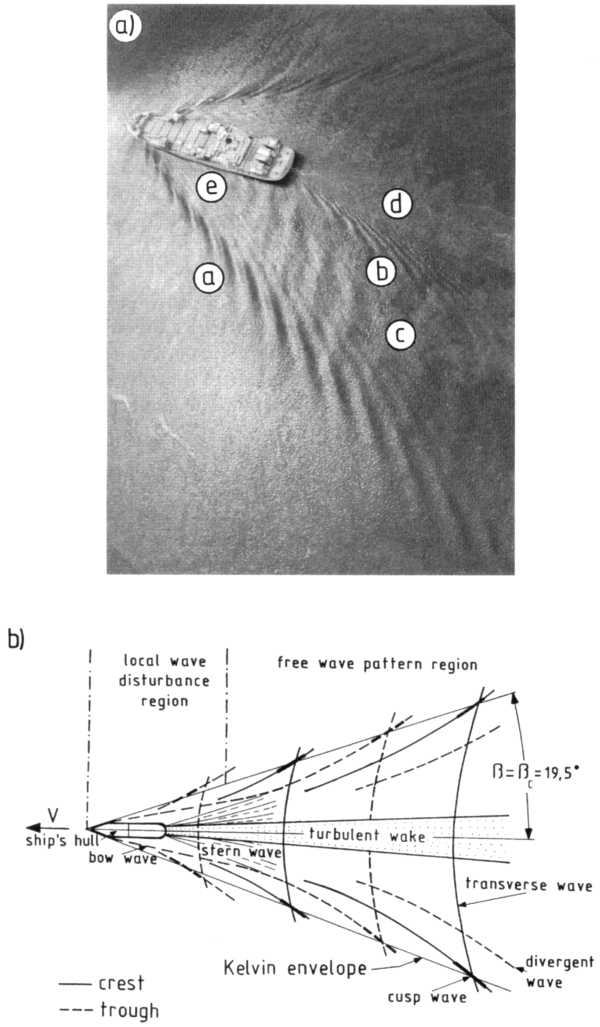
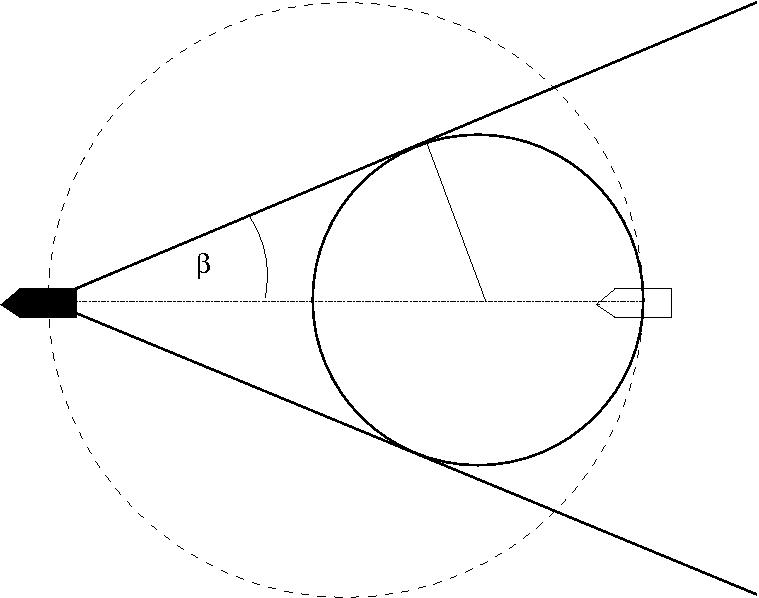
$$\sin \beta= \frac{1}{3}\quad \Rightarrow \quad \beta = 19^\circ 28'$$

Hajóhullámok a felhőzetben. A hajó szerepét itt az Amszterdam-sziget
játssza (Indiai-óceán)

William Thomson (Lord Kelvin), (1824-1907)
9.6. Kapilláris hullámok.
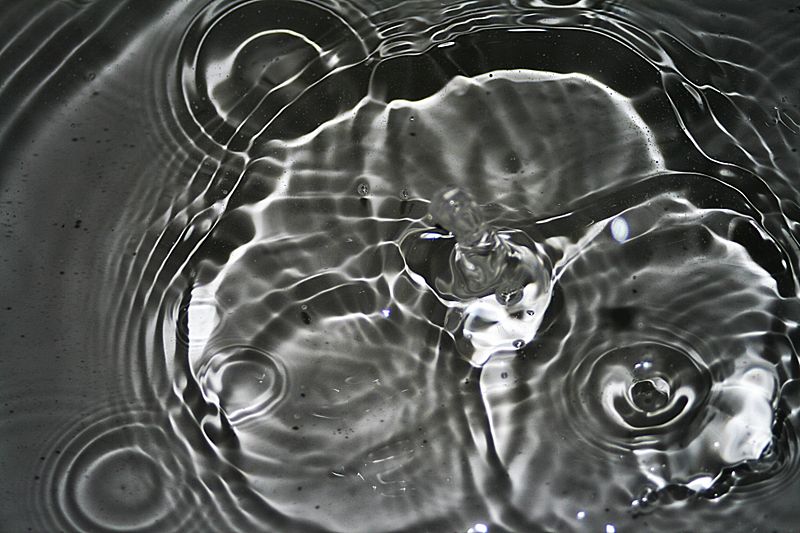
Esőcseppek becsapódása által keltett kapilláris hullámok
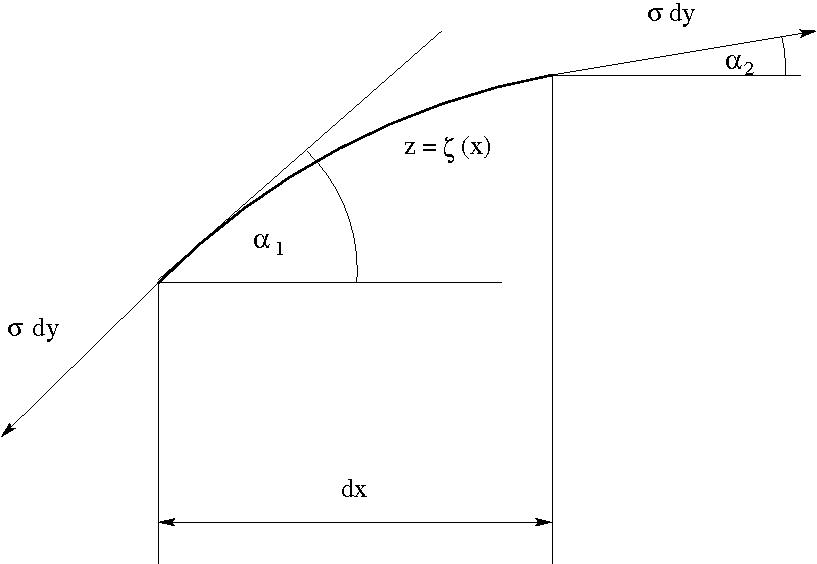
A felületi feszültségből eredő nyomás:
$$
\Delta p=\frac{\sigma dy (\alpha_1-\alpha_2)}{dy\;dx/\cos \alpha_1}=-\sigma \frac{\zeta''}{\left(1+\zeta'^2\right)^{\frac{3}{2}}}
$$
Lineáris vízhullámok esetén a egyenletek:
$$\triangle \Phi=0$$
$$\frac{\partial \Phi}{\partial t}+\frac{p+\Delta p-p_0}{\rho}+gz=0$$
Peremfeltételek:
- $$\left.\frac{\partial \Phi}{\partial z}\right|_\zeta=\frac{\partial \zeta}{\partial t}=\dot z$$
-
$$\left.\frac{\partial \Phi}{\partial t}\right|_\zeta+g\zeta-\frac{\sigma}{\rho}\zeta''=0$$
- A fenti két peremfeltételből következik, hogy
$$\left.\left(\frac{\partial^2 \Phi}{\partial t^2}+g\frac{\partial \Phi}{\partial z}-\frac{\sigma}{\rho}\frac{\partial^3 \Phi}{\partial z\partial x^2}\right)\right|_\zeta=0$$
-
$$\left.\frac{\partial \Phi}{\partial z}\right|_{z=-h}=0$$
A megoldás ismét
$$\Phi(x,z,t)=A\cos(kx-\omega t)\;{\rm ch}\;k(z+h)$$
Ezt a felszínen felírt Bernoulli-egyenletbe betéve:
$$-\omega^2 \;{\rm ch}\;k(\zeta +h)+gk\;{\rm sh}\;k(\zeta
+h)+\frac{\sigma}{\rho}k^3\;{\rm sh}\;k(\zeta +h)=0$$
Mivel $\zeta\ll h$, azt kapjuk, hogy
$$
\omega(k)=\sqrt{\left(gk+\frac{\sigma}{\rho}k^3\right){\rm th}\;kh}
$$
Kapilláris hullámok mély víz felszínén:
$$\omega(k)=\sqrt{gk+\frac{\sigma}{\rho}k^3}$$
Itt $\sigma$ a felületi feszültség.
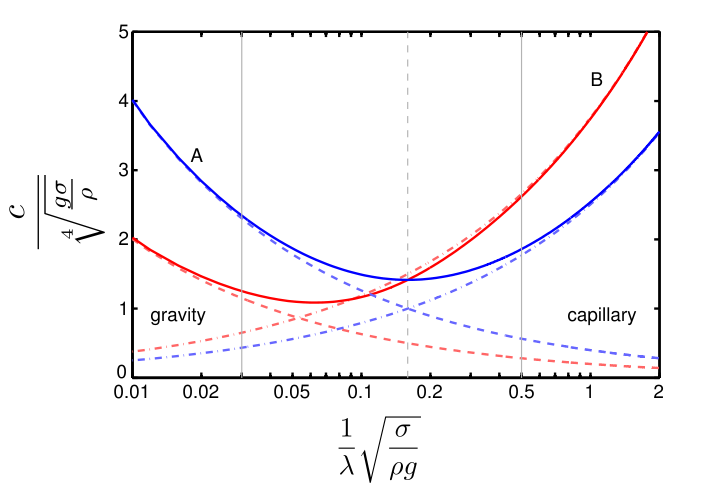
Kapilláris hullámok fázis- és csoportsebessége a hullámszám
függvényében. Fázissebesség: kék, csoportsebesség: piros
Fázissebesség:
$$c(k)=\sqrt{\frac{g}{k}+\frac{\sigma}{\rho}k}$$
Csoportsebesség:
$$c_g(k)=\frac{g+3\frac{\sigma}{\rho}k^2}{2\sqrt{gk+\frac{\sigma}{\rho}k^3}}=\frac{3}{2}c(k)-\frac{g/k}{c(k)}$$
9.7. Nemlineáris hullámok sekély vízben.
A Korteweg-de Vries-egyenlet
$$\frac{\partial \zeta}{\partial t}+c\left(\frac{\partial \zeta}{\partial
x}+\frac{3}{2h}\zeta\frac{\partial \zeta}{\partial
x}+\frac{h^2}{6}\frac{\partial^3 \zeta}{\partial x^3}\right)=0$$
Itt $c=\sqrt{gh}$.
Szoliton
$$\zeta(x,t)=\underbrace{\frac{v_0^2-c^2}{g}}_{A \text{
amplitudó}}\frac{1}{\text{ch}^2\left[\sqrt{\frac{3}{4}\frac{v_0^2-c^2}{c^2h^2}}(x-v_0t)\right]}$$
Ez a nemlinearitás miatt megőrzi alakját, nem folyik szét.
$$v_0^2=g(h+A)$$
A sebesség az amplitudótól függ, és nagyobb a lineáris hullámok maximális
$c=\sqrt{gh}$ sebességénél (bár csak kicsivel, mivel
$v_0\approx c\left(1+\frac{1}{2}\frac{A}{h}\right)$ és $A\ll h$ ).
A szoliton felfedezése: John Scott Russell, 1834.

Csónak megállása után vízdomb, kb. 14 km/h-val halad,
szélessége ~7 m, magassága ~0.4 m. A vízmélység 1.1 m volt. Negyedórán át tudta
követni lóháton.
Későbbi kísérletek. A legjobb keltési mód: kő
vízbeejtése.

A nagyobb szoliton utoléri és megelőzi a
kisebbet. A szolitonok ütközéskor megőrzik alakjukat.
10.2. Súrlódó folyadékok
- A súrlódási tenzor
A kiszemelt folyadékrész határán felületi erők hatnak. Eredőjük felületi
integrál. Ezt átírjuk térfogativá (szükséges a mozgásegyenlethez).
$\int_V \tilde{{\bf F}} dV$ adja a felületi erők járulékát.
$\tilde{{\bf F}}$ ezért előáll divergenciaként. Mivel
$\tilde{{\bf F}}$ vektor:
$$\tilde{{\bf F}}=\text{div }{\bf \sigma}_i\equiv \sum_{k=1}^3
\frac{\partial \sigma_{ik}}{\partial x_k}\quad i=1,2,3$$
$\sigma_{ik}$ : feszültségtenzor
$$\int_V \tilde{F}_i dV=\oint_F\sum_k \sigma_{ik} dF_k=\oint_F\sum_k
\sigma_{ik} n_k dF$$
Itt $n_k$ a felületelem normálisának $k$-adik komponense.
$\sigma$ jelentése: Az ${\bf n}$ irányú (normálisú) egységnyi
felületre ható erő $\underline{\underline{\sigma}}{\bf n}$.
Ha
$${\bf n}=\left(\begin{array}{c}1\\0\\0\end{array}\right)\;,$$
akkor $\left(\underline{\underline{\sigma}}{\bf n}\right)_i=\sigma_{i1}$
$\sigma_{ik}$ tehát a $k$ irányú (normálisú) egységnyi
felületre ható erő $i$-edik komponense.
Ideális folyadékban ill. hidrosztatikában:
$$\sigma_{ik}=-p\delta_{ik}$$
Nincsenek nyírófeszültségek.
Súrlódó folyadékban vannak nyírófeszültségek is. Az előzőtől való eltérés a
sebességkülönbségből adódik, s azzal arányos (hacsak nem túl nagy a
sebességkülönbség).
$$\sigma_{ik}=-p\delta_{ik}+\sigma'_{ik}$$
$$\sigma'_{11}\propto \frac{\partial v_x}{\partial x}$$
$$\sigma'_{21}=\alpha \frac{\partial v_y}{\partial x}+\beta \frac{\partial
v_x}{\partial y}$$
A merev forgás nem jelenthet új feszültséget:
Ha $v_x=-\omega y$, $v_y=\omega x$ (forgás az $x$ tengely körül), akkor
$$ \sigma'_{21}=\alpha\omega-\beta\omega=0\quad\Rightarrow\quad\alpha=\beta$$
Ha van térfogatváltozás (nem összenyomhatatlan), akkor $\text{div
}{\bf v}$-vel arányos tag is fellép a diagonális elemekben.
Az általános alak:
$$\sigma_{ik}=-p\delta_{ik}+\eta\left(\frac{\partial v_i}{\partial x_k}+\frac{\partial v_k}{\partial x_i}\right)+\eta'\text{div
}{\bf v}\delta_{ik}$$
$\eta$ : dinamikai viszkozitás.
$\eta'$ helyett más szokásos mennyiség: $\eta'=\xi-\frac{2}{3}\eta$, ahol
$\xi$ neve: belső súrlódási együttható.
$\eta$ és $\eta'$ minden komponensben ugyanakkora az izotrópia miatt.
Folyadékkristályban ez nem lenne igaz.
- A Navier-Stokes-egyenletek
$$\int \rho\frac{d {\bf v}}{dt}dV=\int
\rho{\bf f}dV+\int\tilde{{\bf F}}dV
\text{ tetszőleges véges $V$ térfogatra.}$$
$$\Downarrow$$
$$\rho\frac{d
{\bf v}}{dt}=\rho{\bf f}+\tilde{{\bf F}}=\rho{\bf f}+\text{div
}\underline{\underline{\sigma}}$$
$$\tilde{F}_1=\frac{\partial \sigma_{11}}{\partial x}+\frac{\partial
\sigma_{12}}{\partial y}+\frac{\partial \sigma_{13}}{\partial
z}=-\frac{\partial p}{\partial x}+2\eta \frac{\partial^2 v_x}{\partial x^2}+\eta'\frac{\partial }{\partial x}\text{div
}{\bf v}+\eta\left(\frac{\partial^2 v_y}{\partial x\partial
y}+\frac{\partial^2 v_x}{\partial y^2}\right)+\eta\left(\frac{\partial^2
v_z}{\partial x\partial z}+\frac{\partial^2 v_x}{\partial
z^2}\right)=-\frac{\partial p}{\partial x}+\eta\triangle v_x+(\eta+\eta')\frac{\partial }{\partial x}\text{div
}{\bf v}$$
$$\Downarrow$$
$$\rho\frac{d
{\bf v}}{dt}=\rho\frac{\partial
{\bf v}}{\partial
t}+\rho({\bf v}\text{grad}){\bf v}=\rho{\bf f}-\text{grad }p+\eta\triangle {\bf v}+(\eta+\eta')\text{grad }\text{div
}{\bf v}$$
Ezek a Navier-Stokes-egyenletek (1822, 1845).
Összenyomhatatlan folyadékban
$$\frac{\partial
{\bf v}}{\partial
t}+({\bf v}\text{grad}){\bf v}={\bf f}-\frac{1}{\rho}\text{grad
}p+\nu\triangle {\bf v}$$
Itt $\nu=\frac{\eta}{\rho}$ a kinematikai viszkozitás.
Mivel
$$\triangle {\bf v}=\text{grad }\text{div
}{\bf v}-\text{rot }\text{rot
}{\bf v}\;,$$
ha a viszkozitásnak szerepe van, az áramlás nem lehet örvénymentes!
Határfeltételek:
Nyugvó fal: ${\bf v}=0$, mozgó fal:
${\bf v}={\bf v}_{\text{fal}}$.
Nem csak a normális, hanem a tangenciális komponensre is van feltétel! (A
Navier-Stokes-egyenletek másodrendűek, szemben az elsőrendű Euler-egyenlettel.)
Ha a felületre ható erő adott, akkor a felületen $\sum_k\sigma_{ik}n_k$-t
kell vele egyenlővé tenni.
- Lamináris áramlás egymáshoz képest párhuzamosan mozgó síklapok
között
Ha a felső lap az alsóhoz képest $\bf u$ sebességgel mozog és $d$ a lapok
távolsága, akkor
$${\bf v}={\bf u}\frac{z}{d}$$
valamint $p=const.$ Valóban, így mind a határfeltétel, mind a
Navier-Stokes-egyenlet teljesül.
A lapok felületegységére ható erő (nyírófeszültség):
$$\frac{{\bf F}}{A}=\pm \eta\frac{{\bf u}}{d}$$
- Lamináris áramlás álló síklapok között nyomásgradiens hatására
Ezúttal ${\bf v}=0$ érvényes mind $z=0$, mind $z=d$ esetén. Mivel ${\bf
\nabla} p$ nullától különböző állandó, stacionárius áramlás esetén a
Navier-Stokes-egyenlet
$$0=-\frac{1}{\rho}\text{grad }p+\frac{\eta}{\rho}\triangle {\bf v}=0$$
alakra redukálódik. Ebből
$$ {\bf v}=\frac{1}{2\eta}\left(z-\frac{d}{2}\right)^2\text{grad }p\;+{\bf
v}_0(1-bz)$$
A ${\bf v}_0$ és $b$ állandókat a határfeltételből kapjuk:
$z=0$ esetén ${\bf v}=\frac{d^2}{8\eta}\text{grad }p+{\bf
v}_0=0$, ebből
$${\bf v}_0=-\frac{d^2}{8\eta}\text{grad }p$$
Másrészt $z=0d$ esetén ${\bf v}=\frac{d^2}{8\eta}\text{grad }p+{\bf
v}_0(1-bd)=0$, ebből
$$b=0$$
Tehát végül
$${\bf v}=\frac{1}{2\eta}z(z-d)\text{grad }p\;$$
- Lamináris áramlás csőben: a Hagen-Poiseuille-egyenlet
Hengerkordináták, a $z$ tengely legyen a cső szimmetriatengelye.
A sebességnek csak $z$ komponense van, és csak $r$-től függ. Ezzel
$$\text{div }{\bf v}=\frac{1}{r}\frac{\partial rv_r}{\partial
r}+\frac{1}{r}\frac{\partial v_\varphi}{\partial \varphi}+\frac{\partial
v_z}{\partial z}=0$$
automatikusan teljesül, továbbá
$${\bf v}\text{grad }{\bf v}=v_z\frac{\partial {\bf v}}{\partial z}=0$$
Mivel az áramlás stacionárius,
$$\frac{\partial {\bf v}}{\partial t}=0$$
A Navier-Sokes-egyenlet ezekután a
$$0=-\frac{1}{\rho}\text{grad }p+\frac{\eta}{\rho}\triangle {\bf v}=0$$
egyenletre egyszerűsödik.
Az egyenlet $r$ komponense:
$$\frac{\partial p}{\partial r}=0$$
Ebből
$$p=p(z)$$
Az egyenlet $z$ komponense:
$$\frac{d p}{d z}=\eta\frac{1}{r}\frac{d}{d r}\left(r\frac{d v_z}{d r}\right)$$
A jobboldal csak $r$ függvénye, ezért
$$p=az+b$$
ahol $a$ és $b$ állandók. Ha az $L$ hosszúságú cső végei közt a nyomáskülönbség
nagysága $\Delta p$, és a nyomás növekvő $z$-vel csökken, akkor
$ \Delta p=-aL$, azaz
$$a=-\frac{\Delta p}{L}$$
Ezzel
$$\frac{1}{r}\frac{d}{d r}\left(r\frac{d v_z}{d
r}\right)=-\frac{\Delta p}{\eta L}$$
$r$-rel szorzunk:
$$\frac{d}{d r}\left(r\frac{d v_z}{d
r}\right)=-\frac{\Delta p}{\eta L}r$$
Integrálunk:
$$r\frac{d v_z}{d
r}=-\frac{\Delta p}{2\eta L}r^2+C$$
Itt $C$ integrációs állandó.
$r$-rel osztunk:
$$\frac{d v_z}{d
r}=-\frac{\Delta p}{2\eta L}r+\frac{C}{r}$$
Integrálunk:
$$v_z=-\frac{\Delta p}{4\eta L}r^2+C\ln r+D$$
Itt $D$ újabb integrációs állandó. Mivel $r=0$ esetén $v_z$ véges kell, hogy
legyen,
$$C=0\;.$$
A cső falán, $r=R$ esetén $v_z=0$, ebből
$$D=\frac{\Delta p}{4\eta L}R^2$$
Tehát a sebességprofil
$$v_z=\frac{\Delta p}{4\eta L}(R^2-r^2)$$
A másodpercenként átáramló folyadéktérfogat
$$\frac{dV}{dt}=\int_0^R v_z\;2\pi r dr =\frac{\pi\Delta p}{2\eta L}\int_0^R
(R^2-r^2)r dr=\frac{\pi\Delta p}{2\eta
L}\left.\left(R^2\frac{r^2}{2}-\frac{r^4}{4}\right)\right|_{r=0}^{r=R}=\frac{\pi
R^4 \Delta
p}{8\eta L}$$
Tehát
$$\frac{dV}{dt}=\frac{\pi R^4 \Delta p}{8\eta L}$$
- Gömbre ható erő lassú lamináris áramlás esetén: a Stokes-képlet
$${\bf F}=6\pi\eta R{\bf u}$$
- A hidrodinamika hasonlósági törvénye
A Navier-Stokes-egyenlet dimenziótlanítása és a Reynolds-szám
$${\bf r}=L\tilde{{\bf r}}$$
$${\bf v}=U\tilde{{\bf v}}$$
$$t=\frac{L}{U}\tilde{t}$$
$$p=\rho U^2\tilde{p}$$
A dimenziótlan változókkal a Navier-Stokes-egyenlet (ha a térfogati erő nulla):
$$\frac{\partial \tilde{{\bf v}}}{\partial \tilde{t}}+(\tilde{{\bf v}}\tilde{\text{grad}})\tilde{{\bf v}}=-\tilde{\text{grad
}}\tilde{p}+\frac{\nu}{UL}\tilde{\triangle} \tilde{{\bf v}}$$
Reynolds-szám:
$$\text{Re}=\frac{UL}{\nu}$$
- A turbulencia megjelenése
Lineáris stabilitásvizsgálat.
Legyen ${\bf v}_0$ és $p_0$ a Navier-Stokes-egyenletek adott határfeltételt
teljesítő egzakt megoldása. Adjunk ehhez kis perturbációt:
$${\bf v}={\bf v}_0+{\bf v}_1\;,\quad p=p_0+p_1$$
A kis perturbációs tagok szerint lineáris rendben kapjuk:
$$
\begin{eqnarray}
\frac{\partial {\bf v}_1}{\partial t}+({\bf v}_1\cdot{\bf \nabla}){\bf
v}_0+({\bf v}_0\cdot{\bf \nabla}){\bf v}_1&=&-\frac{{\bf \nabla} p_1}{\rho}+\nu\triangle {\bf v}_1\\
{\bf \nabla}\cdot{\bf v}_1&=&0
\end{eqnarray}
$$
A határfeltételek ugyanazok ${\bf v}_1$-re, mint ${\bf v}_0$-ra.
- Ha az
alapmegoldás stacionárius, akkor ${\bf v}_1={\bf u}({\bf r})e^{i\omega t}$
alakú megoldások léteznek. A stabilitás feltétele, hogy $\omega$ képzetes
része semelyik módusra ne legyen negatív. Instabilitás esetén a perturbáció
növekszik, a nemlineáris tagok pedig stabilizálják az eredetileg instabil
módust, periodikus mozgás alakul ki.
- Ha az alapmegoldás periodikus, ${\bf v}_1={\bf u}({\bf r},t)e^{i\omega
t}$, ahol ${\bf u}({\bf r},t)$ az alapmegoldás körfrekvenciájával
periodikus. Az alapmegoldás körfrekvenciája és $\omega$ aránya általában
irracionális (kváziperiodikusság). Instabilitás esetén a perturbáció
növekszik, a nemlineáris tagok pedig stabilizálják az eredetileg instabil
módust, kváziperiodikus mozgás alakul ki.
- Ha az alapmegoldás kváziperiodikus, ${\bf v}_1$-ben ismét újabb frekvencia
jelenik meg, a megoldás azonban instabilitás esetén a perturbáció növekedtével
nem stabilizálódik, hanem tipikusan kaotikussá válik.
- Nagy Reynolds-számok esetén a mozgás jellegzetes kavargó, aperiodikus,
véletlenszerű: turbulens. A turbulencia kvantitatív elmélete nincs kidolgozva.
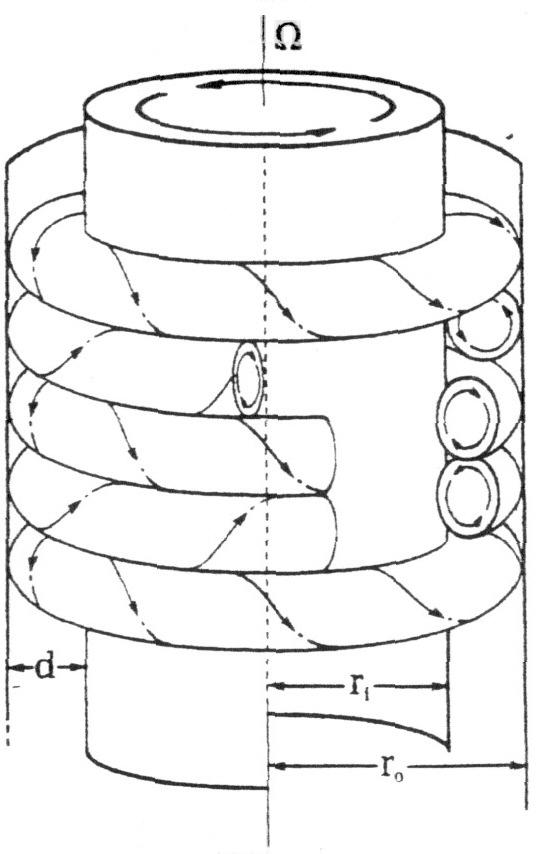
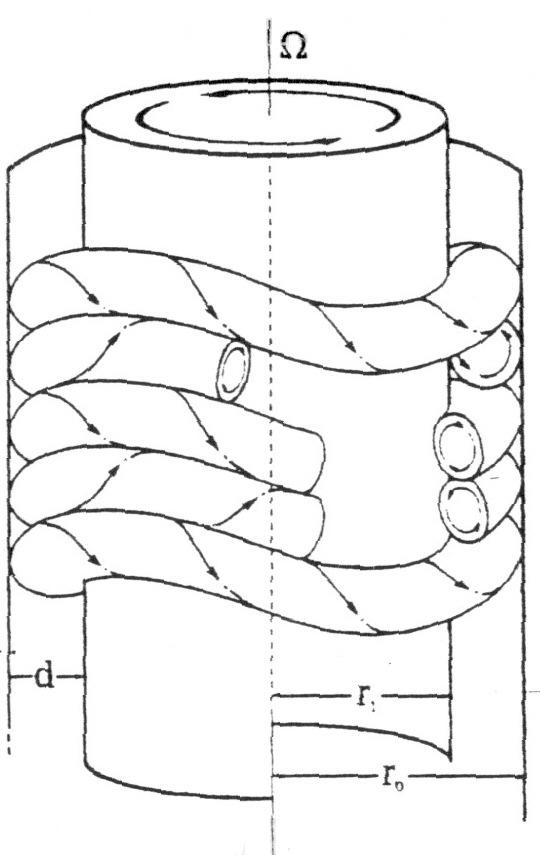
- Áramlás koncentrikus, forgó hengerek közt (Couette-Taylor-áramlás)
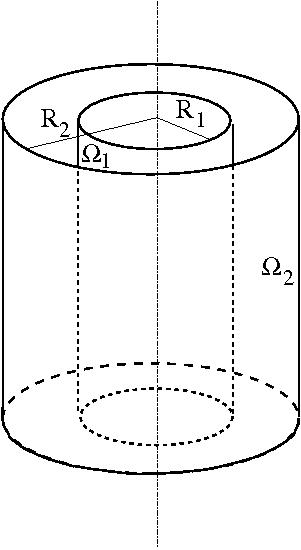
-
Henger körüli áramlás:

Re=9.6

Re=26
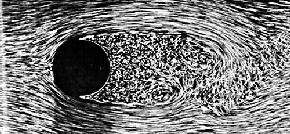
Re=2000

Re=10000
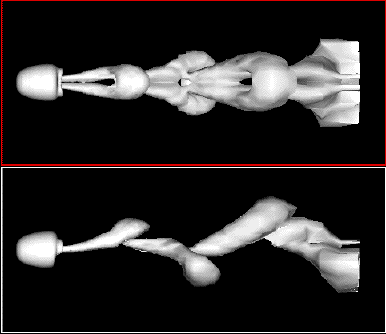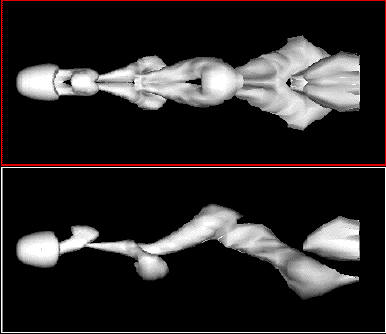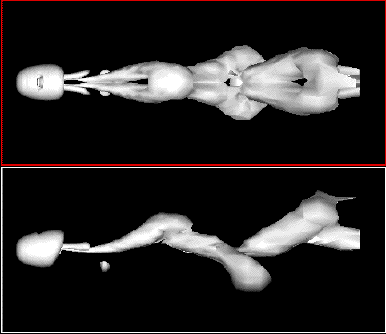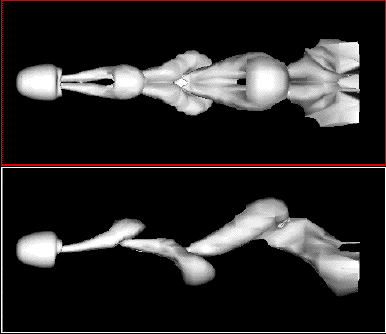
Örvények leválása gömbről, szimuláció, Re=300
- Lamináris vs. turbulens áramlás





 bene@arpad.elte.hu
bene@arpad.elte.hu