


Inhomogén univerzum tágulása
Szerkezetkialakulás (szimuláció)
$$\rho_m=\rho_{m0}(1+z)^3$$
$$\rho_\Lambda=\rho_{\Lambda 0}$$
$$\Downarrow$$
$$\frac{\Omega_\Lambda}{\Omega_m}=\frac{\Omega_{\Lambda0}}{\Omega_{m0}}\frac{1}{(1+z)^3}$$
A nemrelativisztikus anyag és a sötét energia (kozmológiai állandó) járuléka $z=0.46$-nál válik egyenlővé. Az első kvazárok $z=6$ körül (szimulációkban már $z=16$
körül) alakulnak ki. Mire az Univerzum kozmológiai állandó-dominálttá válik,
a szerkezetkialakulás már előrehaladott, nagyok a sűrűségfluktuációk.
Okozhatja-e a gyorsuló tágulást az inhomogenitás? (v.ö.: G.Ellis, Nature
452, 158, (2008).)
Perturbatív vizsgálat
(Gy.B., V.Czinner, M.Vasúth, Modern Physics Letters A, 21, 1117-1125
(2006). és astro-ph/0308161)
$
\begin{eqnarray}
\overline{g_{ik}}(t)=\lim_{V\rightarrow \infty} \frac{1}{V}\int_V d^3 \boldsymbol r\; g_{ik}(t,\boldsymbol r)\; .
\end{eqnarray}
$
$
\begin{eqnarray}
R_{ik}(\{g_{ik}\})-\frac{1}{2}g_{ik} R(\{g_{ik}\})=\frac{8\pi G}{c^4} T_{ik}
\end{eqnarray}
$
$
\begin{eqnarray}
g_{jk}=g_{jk}^{(0)}+g_{jk}^{(1)}+g_{jk}^{(2)}
\end{eqnarray}
$
$
\begin{eqnarray}
\overline{g_{00}}(t)=c^2\; ,\\
\overline{g_{0\alpha}}(t)=0\; ,\\
\overline{g_{\alpha\beta}}(t)=-R^2(t)\delta_{\alpha\beta}
\end{eqnarray}
$
$
\begin{eqnarray}
\overline{g_{\alpha\beta}^{(i)}} = -\delta_{\alpha\beta}\left(R^2\right)^{(i)}(t) \ , \qquad i=0,1,2
\end{eqnarray}
$
$
\begin{eqnarray}
T^{00}=\rho=\rho^{(0)}+\rho^{(1)}+\rho^{(2)}\; ,\\
T^{0\alpha}=0\; ,\\
T^{\alpha\beta}=0\; .
\end{eqnarray}
$
$
\begin{eqnarray}
R^{(0)}&=&\frac{2c}{H_0}\left(\frac{3}{2}H_0t\right)^{\frac{2}{3}}\;,\\
\rho^{(0)}&=&\frac{1}{6\pi G t^2}\;.
\end{eqnarray}
$
$
\begin{eqnarray}
g^{(1)}_{\alpha \beta} &=& \frac{4c^2\eta^4}{H_0^2}\left[{ 1 \over \eta}\;
{ \partial \over \partial \eta}\; \left({ 1 \over \eta}\;
D_{\alpha \beta} \right)\right. \\\left.\right. &&\left.\; - 2 \left({ 8 \over \eta^3}
-{ \Delta \over \eta} \right)( C_{\alpha,\beta } +C_{\beta,\alpha} ) \right. \\
\left.\right. &&\left.\;+{ A_{ ,\alpha\beta}\over \eta^3}+\eta_{\alpha \beta} B -
{ \eta^2\over 10} B_{ , \alpha\beta}\right] \; , \\
g^{(1)}_{\alpha 0} &=& -\frac{4c^2}{H_0} \Delta C_{\alpha}\; , \\
\rho^{(1)}\; &=&\; { H^2_0\over 32\pi G}\;
\Delta \; \left(\; { 6A\over \eta^9} -{3\over 5}
{ B \over \eta^4}\;\right)
\end{eqnarray}
$
$
\begin{eqnarray}
\eta=\left(\frac{3}{2}H_0t\right)^{\frac{1}{3}}\; .
\end{eqnarray}
$
$
\begin{eqnarray}
&& (\rm{terms\quad linear\quad in\quad} g^{(2)}_{ik}) \\
&+&(\rm{terms\quad quadratic\quad in\quad} g^{(1)}_{ik})=8\pi G\;\rho^{(2)}\; .
\end{eqnarray}
$
$
\begin{eqnarray}
&& 6\frac{\dot {R}^{(0)}}{{R}^{(0)}}\left(\frac{\dot {R}^{(2)}}{{R}^{(0)}}-\frac{\dot {R}^{(0)}R^{(2)}}{\left({R}^{(0)}\right)^2}\right)+\frac{1}{400}H_0^2\;\overline{\left(\triangle B\right)^2}\;\frac{1}{\eta^2}
\\
&&-\frac{17}{80}H_0^2\;\overline{\left(\boldsymbol \nabla B\right)^2}\;\frac{1}{\eta^4}
=8\pi G\;\rho^{(2)}\; .
\end{eqnarray}
$
$
\begin{eqnarray}
&&\frac{1}{\left(R^{(0)}\right)^3}\left(\rho^{(2)}\left(R^{(0)}\right)^3\right)_{,0}
-\frac{1}{2}\overline{\rho^{(1)}\left(\frac{g^{(1)}_{\alpha\alpha}}{\left(R^{(0)}\right)^2}\right)_{,0}}
\\
&+&\frac{1}{2}\rho^{(0)}\left\{3\left(2\frac{R^{(2)}}{R^{(0)}}+
\frac{1}{4}\left(\overline B\right)^2\right)_{,0}
-\frac{1}{\left(R^{(0)}\right)^4}\overline{g^{(1)}_{\alpha\beta}g^{(1)}_{\alpha\beta,0}}
\right. \\\left.
\right.&-&\left.\frac{2\dot R^{(0)}}{\left(R^{(0)}\right)^3}\left[\frac{1}{c^2}
\overline{\left(g^{(1)}_{0\alpha}\right)^2}-
\frac{1}{\left(R^{(0)}\right)^2}\overline{\left(g^{(1)}_{\alpha\beta}\right)^2}\right]\right\}=0\; .
\end{eqnarray}
$
$
\begin{eqnarray}
8\pi G \rho^{(2)} =- 6\pi G\rho^{(0)}\left(4\frac{R^{(2)}}{R^{(0)}}+A_1
\right) \\-\frac{3}{20}H_0^2\;\overline{\left(\boldsymbol \nabla B\right)^2}\;\frac{1}{\eta^4}
+\frac{9}{800}H_0^2\;\overline{\left(\triangle B\right)^2}\;\frac{1}{\eta^2}
\end{eqnarray}
$
$
\begin{eqnarray}
\dot R^{(2)} +\frac{1}{3t}R^{(2)}&=&-\frac{3}{4}\frac{c\;A_1}{\left(\frac{3}{2}H_0t\right)^{\frac{1}{3}}}
+\frac{1}{48}\overline{(\boldsymbol \nabla B)^2}c\left(\frac{3}{2}H_0t\right)^{\frac{1}{3}} \\
&+&\frac{7}{1600}\overline{(\triangle B)^2}H_0ct
\end{eqnarray}
$
$
\begin{eqnarray}
R^{(2)}&=&A_2\;t^{-\frac{1}{3}}-\frac{1}{4}A_1 R^{(0)}
+\frac{1}{120}\frac{c}{H_0}\overline{(\boldsymbol \nabla B)^2}\left(\frac{3}{2}H_0t\right)^{\frac{4}{3}} \\
&+&\frac{3}{1600}\overline{\left(\triangle B\right)^2}\;H_0\;c\; t^2
\end{eqnarray}
$
$
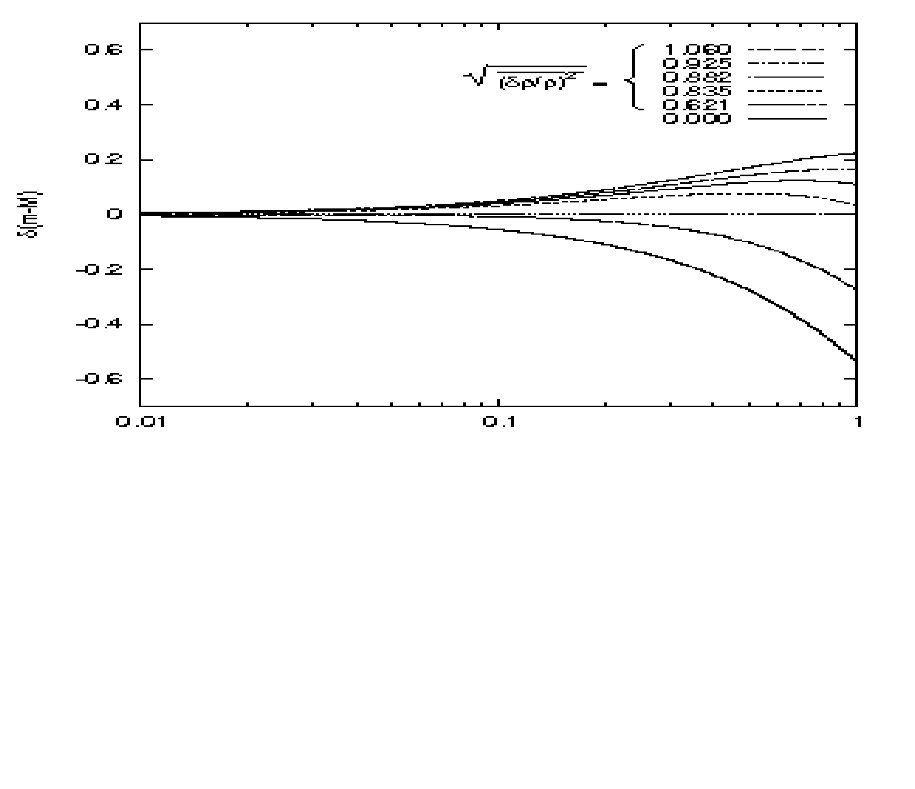
\begin{eqnarray}
R(t)&=&R^{(0)}+\frac{3}{1600}\overline{\left(\triangle B\right)^2}\;H_0\;c\; t^2\\
&=&R^{(0)}\left[1+\frac{1}{6}\overline{\left(\frac{\delta\rho}{\rho}\right)^2} \right]
\end{eqnarray}
$
$
\begin{eqnarray}
\overline{\left(\frac{\delta\rho}{\rho}\right)^2_0} =\overline{ \left(\frac{\delta\rho}{\rho}\right)^2_{dec}} (1+z_{dec})^2 \approx 1...100\;,
\end{eqnarray}
$
$
\begin{eqnarray}
q= -\frac{\ddot{R}R}{\dot{R}^2}= \frac{1}{2}\left[1-\frac{7}{3}\overline{\left(\frac{\delta\rho}{\rho}\right)^2} \right]\; .
\end{eqnarray}
$
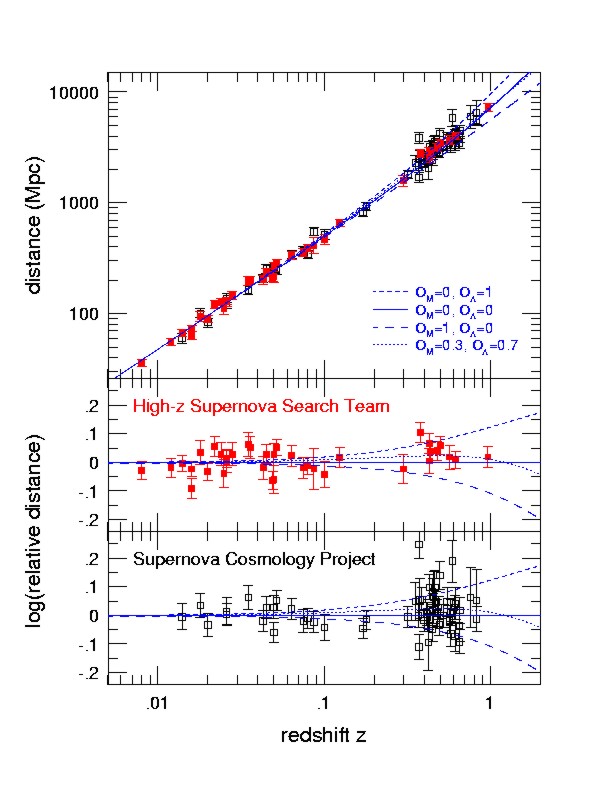
Gyorsuló tágulás $z\approx 0.53$-tól.
$
\begin{eqnarray}
p=-\frac{7c^2}{4800}\left(\frac{H_0^4}{3(\pi G)^2}\right)^{\frac{1}{3}}
\overline{(\triangle B)^2}\rho^{\frac{1}{3}}\;.
\end{eqnarray}
$
$
$
$
$
$
$
Ellenérvek:
-
Az átlagolás nem egyértelmű
-
Swisscheese-model




