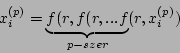Fixpontok és periodikus pontok

A fixpontok az

$$x=f(r,x)$$

egyenlet megoldásai, melyek grafikusan a leképező függvény gráfja és az egységnyi meredekségű egyenes metszéspontjai. Nyilvánvaló, hogy az iterációt egy fixpontból indítva az összes iterált pont azonos marad a kezdőponttal. Ha az egydimenziós leképezés (közelítőleg) egy differenciálegyenlettel leírható fizikai rendszer Poincaré-leképezése, akkor az eredeti rendszer fázisterében a leképezés fixpontja fixpontnak vagy határciklusnak felelhet meg.

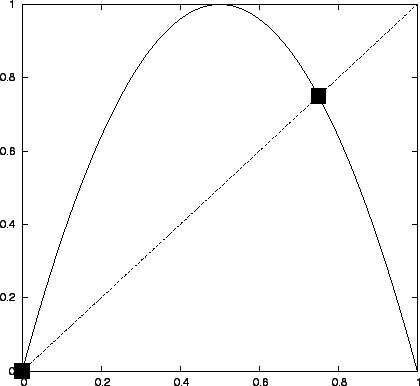
Példa: a logisztikus leképezés fixpontjai.

$$x=rx(1-x)$$

$$x^*_1=0$$

$$x^*_2=1-\frac{1}{r}$$

Grafikusan:

Ábra: A logisztikus leképezés fixpontjai 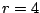$r=4$ esetén.

A fixpontokhoz hasonlóan fontosak a periodikus pontok, amelyek az iteráció hatására egymásba képeződnek:

$$x^{(p)}_2=f(r,x^{(p)}_1)$$

$$x^{(p)}_3=f(r,x^{(p)}_2)$$

$$...$$

$$x^{(p)}_1=f(r,x^{(p)}_p)$$

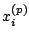Az $x^{(p)}_i$ pontok egy 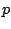$p$ periódusú periodikus pálya, más néven határciklus pontjai. Az egyenletek egymásba helyettesítéséval látható, hogy ezek a pontok egyben kielégítik az

$$x^{(p)}_i=\underbrace{f(r,f(r,...f}_{p-szer}(r,x^{(p)}_i)$$

egyenletet is, tehát a p periódusú periodikus pálya pontjai a p-szer iterált leképezés fixpontjai.

Példa: a logisztikus leképezés 2-es határciklusának pontjai. A megoldandó egyenlet:

$$x=r(rx(1-x))(1-rx(1-x))$$

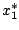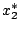Ennek természetesen gyökei az eredeti leképezés fixpontjai, $x^*_1$ és $x^*_2$. Az egyenletet nullára redukáljuk és elosztjuk az 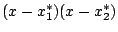$(x-x^*_1)(x-x^*_2)$ másodfokú polinommal. Marad

$$r^2x^2-r(r+1)x+(r+1)=0$$

melynek gyökei

$$x^{(2)}_1=\frac{1}{2r}\left(r+1-\sqrt{r^2-2r-3}\right)$$

és

$$x^{(2)}_2=\frac{1}{2r}\left(r+1+\sqrt{r^2-2r-3}\right)$$

Grafikusan:

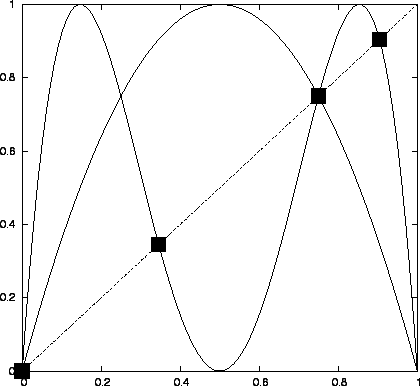
Ábra: A logisztikus leképezés fixpontjai és 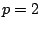$p=2$ periódusú periodikus pontjai 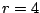$r=4$ esetén.