Fixpontok és periodikus pontok stabilitása

A fixpontot akkor nevezzük stabilnak, ha az elegendően közel indított trajektóriák közelednek hozzá. Ellenkező esetben instabilitásról beszélünk.

Grafikusan:

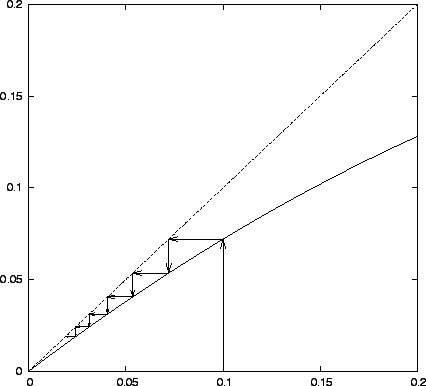
Ábra: Példa stabil fixpontra: a logisztikus leképezés 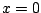$x=0$ fixpontjának környezete 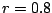$r=0.8$ esetén.

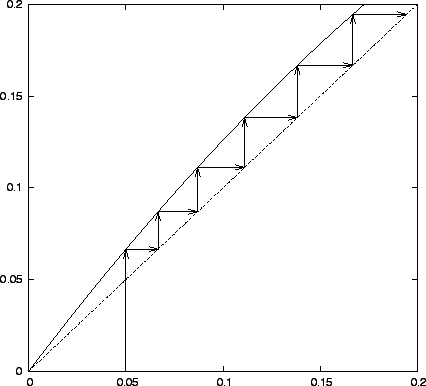
Ábra: Példa instabil fixpontra: a logisztikus leképezés 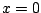$x=0$ fixpontjának környezete 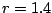$r=1.4$ esetén.

Algebrailag a stabilitás feltételét a következőképpen fogalmazhatjuk meg:

• Legyen 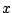$x$ közel az 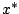$x^*$ fixponthoz. Ekkor
  
  $$f(x)\approx f(x^*)+f'(x^*)(x-x^*)=x^*+f'(x^*)(x-x^*)$$
  
  

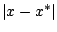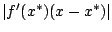• Egy iteráció után a fixpnttól mért távolság tehát $\vert x-x^*\vert$-ról $\vert f'(x^*)(x-x^*)\vert$-ra változott. A fixpont stabil, ha
  
  $$\vert f'(x^*)(x-x^*)\vert<\vert x-x^*\vert$$
  
  
  azaz, ha
  
  $$\vert f'(x^*)\vert<1$$
  
  

• Hasonlóan, a fixpont instabil, ha
  
  $$\vert f'(x^*)\vert>1$$
  
  

• Ha
  
  $$\vert f'(x^*)\vert=1$$
  
  
  akkor a stabilitás vagy instabilitás meghatározásához a magasabb deriváltak ismerete is szükséges. Ilyen esetben marginális stabilitásról ill. instabilitásról beszélünk.

Periodikus pálya stabilitása hasonlóan vizsgálható. A stabilitás feltétele

$$\vert\frac{d}{dx}f^{[p]}(x^{(p)}_i)\vert=\Pi_{i=1}^p \vert f'(x^{(p)}_i)\vert<1$$