Schwarz-derivált:
vagy másképp:
Megjegyzés:
![]() és
és ![]() .
.
-
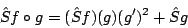
Ui.:
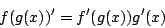
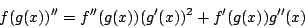
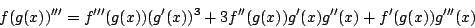
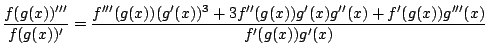
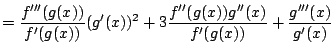
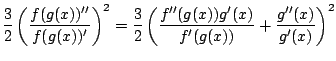
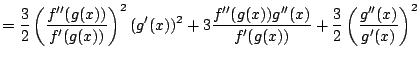
- Feladat: bizonyítsuk be, hogy ha
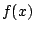 olyan legalább másodfokú
polinom,
melynek minden gyöke valós, akkor
olyan legalább másodfokú
polinom,
melynek minden gyöke valós, akkor 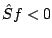 !
!
- Tétel: Ha a leképezés Schwarz-deriváltja negatív, legfeljebb egy stabil periodikus pálya létezhet.
- Tétel: Ha a leképezés Schwarz-deriváltja negatív, és létezik stabil periodikus pálya, akkor egy nullmértékű halmaz kivételével minden pont a stabil periodikus pályához konvergál.
- Tétel: Ha a leképezés Schwarz-deriváltja negatív, és létezik stabil periodikus pálya, akkor a maximum képei a stabil periodikus pályához konvergálnak.