


Next: Hasonlóság. Szuperstabilitás. , .
Up: Egydimenziós leképezések
Previous: Sima maximumú egydimenziós leképezések.
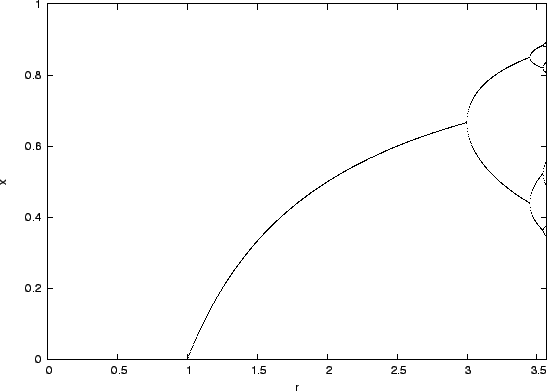
Ábra:
A logisztikus leképezés bifurkációs diagramja 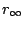 alatt.
alatt.
 |
Legyen 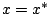 az
az 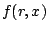 leképezés marginálisan stabil fixpontja (valamilyen rögzített
leképezés marginálisan stabil fixpontja (valamilyen rögzített 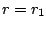 értékre) úgy, hogy
értékre) úgy, hogy
Ekkor
Negatív Schwarz-derivált esetén tehát a második iterált alakja 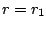 -ben:
-ben:
Ábra:
Perióduskettőző bifurkáció: marginálisan instabil fixpont környezete. (Logisztikus leképezés második iteráltja 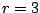 esetén)
esetén)
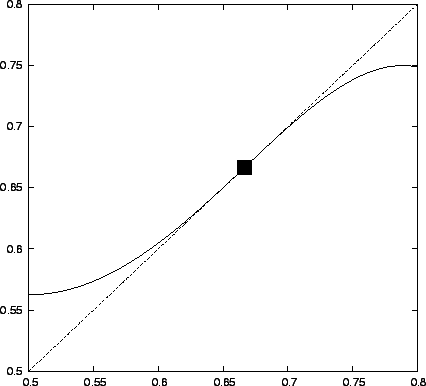 |
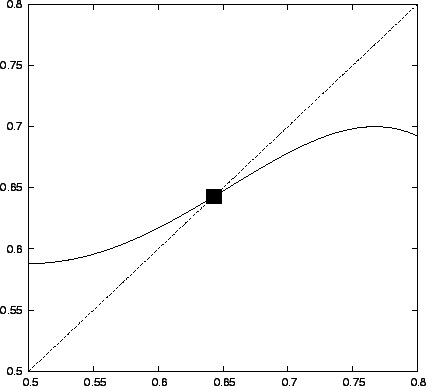
Ábra:
Perióduskettőző bifurkáció. (Logisztikus leképezés második iteráltja 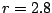 esetén)
esetén)
 |
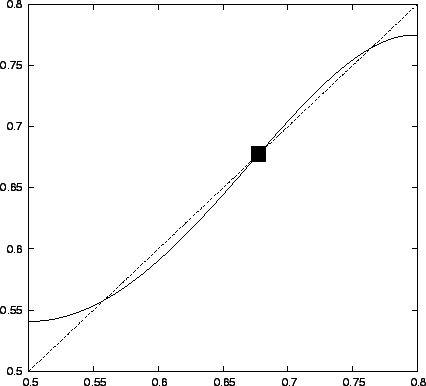
Ábra:
Perióduskettőző bifurkáció. (Logisztikus leképezés második iteráltja 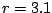 esetén)
esetén)
 |
Bene Gyula
2004-05-10

