


Next: Kaotikus tartomány. Ljapunov-exponens. Káosz
Up: Egydimenziós leképezések
Previous: Perióduskettőző bifurkációk
Szuperstabilitás: bizonyos kontrollparaméter-értékeknél az 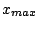 maximumhely
a határciklushoz tartozik. (A logisztikus leképezés esetén
maximumhely
a határciklushoz tartozik. (A logisztikus leképezés esetén
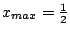 .)
Mivel a sima maximumban a derivált eltűnik,
a ciklus stabilitását jellemző
.)
Mivel a sima maximumban a derivált eltűnik,
a ciklus stabilitását jellemző
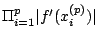 szorzat nulla.
szorzat nulla.
Stabilitási intervallumok a perióduskettőződéseknél: a 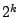 periódusú határciklus stabil az
periódusú határciklus stabil az
kontrollparaméter-intervallumban. Ezen belül a 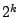 periódusú szuperstabil határciklushoz tartozó kontrollparamétert
periódusú szuperstabil határciklushoz tartozó kontrollparamétert 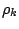 -val jelöljük.
-val jelöljük.
Hasonlóság és univerzalitás:
Ábra:
Hasonlóság: a logisztikus leképezés bifurkációs diagramja kétszer logaritmikus skálán.
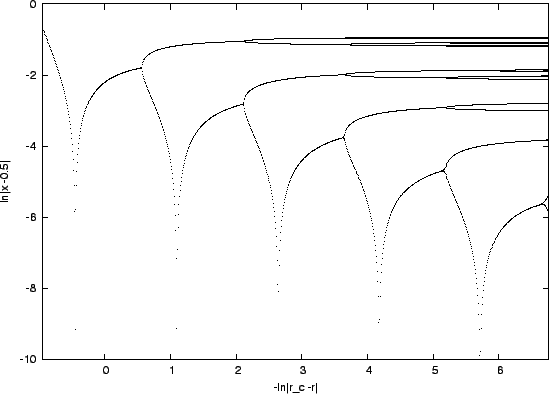 |
- A perióduskettőződés stabilitási intervallumainak hossza geometriai sorozat szerint tart nullához:
A 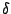 Feigenbaum-állandó a négyzetes maximumú leképezések osztályán univerzális, vagyis
a leképezés konkrét alakjától függetlenül ugyanaz az értéke.
Feigenbaum-állandó a négyzetes maximumú leképezések osztályán univerzális, vagyis
a leképezés konkrét alakjától függetlenül ugyanaz az értéke.
- A szuperstabilitás kontrollparaméter-értékeinél összehasonlítva a bifurkációs villák szélességét, azok is
univerzális kvóciensű geometriai sorozat szerint tartanak a nullához:
Az  Feigenbaum-állandó a négyzetes maximumú leképezések osztályán univerzális, vagyis
a leképezés konkrét alakjától függetlenül ugyanaz az értéke.
Feigenbaum-állandó a négyzetes maximumú leképezések osztályán univerzális, vagyis
a leképezés konkrét alakjától függetlenül ugyanaz az értéke.
Univerzális függvények:
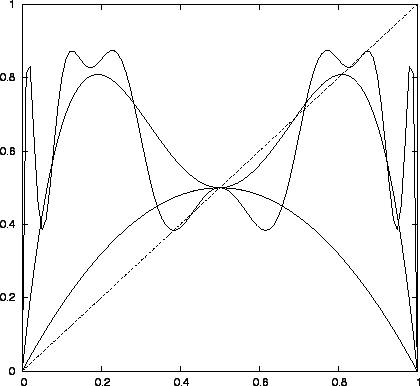
Ábra:
Hasonlóság. (A logisztikus leképezés iteráltjai a szuperstabil pontokban.)
 |
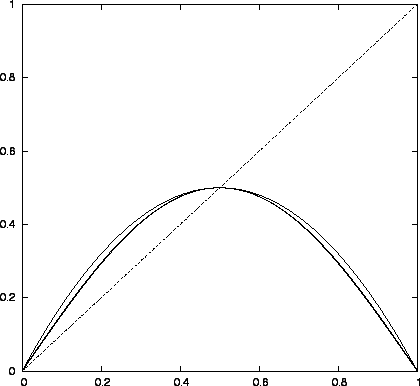
Ábra:
Hasonlóság. (A logisztikus leképezés iteráltjai a szuperstabil pontokban, átskálázva.)
 |
A 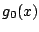 leképezésnek szuperstabil fixpontja van.
leképezésnek szuperstabil fixpontja van.
A 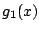 leképezésnek
leképezésnek 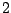 periódusú szuperstabil határciklusa van.
periódusú szuperstabil határciklusa van.
A 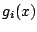 leképezésnek
leképezésnek 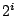 periódusú szuperstabil határciklusa van.
periódusú szuperstabil határciklusa van.
Az egyszerűség kedvéért térjünk át az 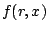 leképezésről az
leképezésről az
leképezésre az
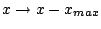 koordinátatranszformációval. Az
koordinátatranszformációval. Az 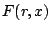 leképezés maximumhelye
leképezés maximumhelye 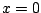 -nál van.
Emiatt
-nál van.
Emiatt
Renormálási transzformáció: A definícióból következően
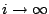 esetén a renormálási transzformáció fixpontját kapjuk (ez nem szám, hanem egy függvény!):
esetén a renormálási transzformáció fixpontját kapjuk (ez nem szám, hanem egy függvény!):
Ha előírjuk, hogy 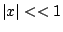 esetén
esetén
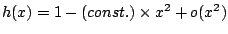 (négyzetes maximum követelménye), akkor
a renormálási transzformáció fixpontegyenlete mind
(négyzetes maximum követelménye), akkor
a renormálási transzformáció fixpontegyenlete mind 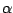 -t, mind
-t, mind 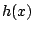 -et meghatározza.
Ez az univerzalitás kifejeződése: az eredeti leképezés konkrét függvényalakja nem befolyásolja pl.
-et meghatározza.
Ez az univerzalitás kifejeződése: az eredeti leképezés konkrét függvényalakja nem befolyásolja pl. 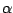 értékét,
csak a maximum környéki viselkedés számít.
értékét,
csak a maximum környéki viselkedés számít.
- Feladat: Közelítsük a 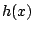 fixpontfüggvényt másodfokú, negyedfokú etc. polinomokkal és a fixpontegyenlet
két oldalán az azonos hatványokat egyenlővé téve határozzuk meg a polinom együtthatóit és az
fixpontfüggvényt másodfokú, negyedfokú etc. polinomokkal és a fixpontegyenlet
két oldalán az azonos hatványokat egyenlővé téve határozzuk meg a polinom együtthatóit és az 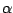 Feigenbaum-állandót!
Feigenbaum-állandót!
Tekintsük most a
leképezést. A 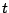 mennyiség a kontrollparaméter,
mennyiség a kontrollparaméter, 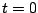 felel meg a perióduskettőző bifurkációk torlódási pontjának,
hiszen
felel meg a perióduskettőző bifurkációk torlódási pontjának,
hiszen 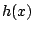 a végtelen periódusú szuperstabil határciklus univerzális függvénye. A
a végtelen periódusú szuperstabil határciklus univerzális függvénye. A 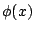 függvényt később
konkretizáljuk.A
függvényt később
konkretizáljuk.A 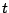 kontrollparaméterrel
alkalmas módon nullához tartva a
kontrollparaméterrel
alkalmas módon nullához tartva a 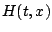 leképezés stabil határciklusai is
perióduskettőző bifurkációk sorozatán mennek keresztül. A szuperstabil pontokat
leképezés stabil határciklusai is
perióduskettőző bifurkációk sorozatán mennek keresztül. A szuperstabil pontokat 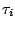 -vel jelöljük.
A renormálási transzformációt a
-vel jelöljük.
A renormálási transzformációt a
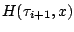 függvényre alkalmazva
függvényre alkalmazva 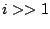 esetén azt kapjuk, hogy
esetén azt kapjuk, hogy
ahol 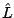 a linearizált renormálási transzformáció, expliciten a következő lineáris operátor:
a linearizált renormálási transzformáció, expliciten a következő lineáris operátor:
Mivel a
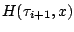 leképezésnek
leképezésnek 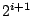 periódusú szuperstabil határciklusa van, a renormálási
transzformáció eredményeként kapott leképezésnek
periódusú szuperstabil határciklusa van, a renormálási
transzformáció eredményeként kapott leképezésnek 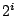 periódusú szuperstabil határciklusa van.
Alkalmas
periódusú szuperstabil határciklusa van.
Alkalmas 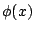 függvény esetén ez azonos lesz a
függvény esetén ez azonos lesz a
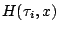 leképezéssel. Matematikailag ez azt jelenti,
hogy
leképezéssel. Matematikailag ez azt jelenti,
hogy
Az egymást követő szuperstabil kontrollparaméter-értékeknek a torlódási ponttól mért távolságai tehát
a linearizált renormálási transzformáció (legnagyobb) sajátértékével adott arányban állnak egymással.
Más szóval a 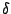 Feigenbaum-állandó a fixpont-függvénye körül linearizált renormálási transzformáció
legnagyobb sajátértéke.
Bár a levezetést speciális esetre végeztük el, az állítás sokkal általánosabban is érvényes.
Feigenbaum-állandó a fixpont-függvénye körül linearizált renormálási transzformáció
legnagyobb sajátértéke.
Bár a levezetést speciális esetre végeztük el, az állítás sokkal általánosabban is érvényes.



Next: Kaotikus tartomány. Ljapunov-exponens. Káosz
Up: Egydimenziós leképezések
Previous: Perióduskettőző bifurkációk
Bene Gyula
2004-05-10
![]() periódusú határciklus stabil az
periódusú határciklus stabil az
![\begin{displaymath}\alpha=\lim_{k\rightarrow \infty} \frac{\left\vert f^{\left[2...
...\right]}(\rho_{k+1},x_{max})-x_{max}\right\vert}=2.502907875...\end{displaymath}](img89.png)
![]() leképezésről az
leképezésről az ![$\displaystyle \lim_{k\rightarrow \infty} (-\alpha)^{(k+1)} F^{\left[2^{k+1}\right]}\left(\rho_{k+1+i},
\frac{x}{(-\alpha)^{(k+1)}}\right)$](img108.png)
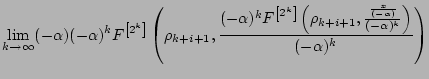
![$\displaystyle (-\alpha) g_{i+1}\left[g_{i+1}\left[\frac{x}{(-\alpha)}\right]\right]$](img110.png)
![]() fixpontfüggvényt másodfokú, negyedfokú etc. polinomokkal és a fixpontegyenlet
két oldalán az azonos hatványokat egyenlővé téve határozzuk meg a polinom együtthatóit és az
fixpontfüggvényt másodfokú, negyedfokú etc. polinomokkal és a fixpontegyenlet
két oldalán az azonos hatványokat egyenlővé téve határozzuk meg a polinom együtthatóit és az ![]() Feigenbaum-állandót!
Feigenbaum-állandót!