


Next: Mérési axiómák
Up: Kvantummechanika dióhéjban
Previous: Kvantummechanika dióhéjban
A klasszikus mechanikában egy fizikai rendszer adott pillanatbeli
állapotán a rendszert alkotó tömegpontok koordinátáinak és
sebességeinek összességét értjük, melyekből a mozgásegyenletek
segítségével lehet (zárt rendszer esetén) a későbbi állapotot
meghatározni. A kvantummechanikában ezzel szemben az állapot az
absztrakt Hilbert-tér egy eleme.6
Jelöljük ezt 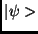 -vel7. A mozgásegyenlet a (zárt rendszerre érvényes)
Schrödinger-egyenlet,
-vel7. A mozgásegyenlet a (zárt rendszerre érvényes)
Schrödinger-egyenlet,
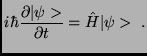 |
|
|
(1) |
A fizikai mennyiségeknek a kvantummechanikában önadjungált lineáris
operátorok8
felelnek meg. Az (1) Schrödinger-egyenletben szereplő
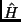 operátor az energia operátora (más néven a Hamilton-operátor).
Egy részrendszer állapotát a kvantummechanikában rendszerint
nem lehet állapotvektorral jellemezni, ehelyett az állapot
jellemzésére a sűrűségmátrix használható. A
operátor az energia operátora (más néven a Hamilton-operátor).
Egy részrendszer állapotát a kvantummechanikában rendszerint
nem lehet állapotvektorral jellemezni, ehelyett az állapot
jellemzésére a sűrűségmátrix használható. A
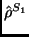 sűrűségmátrix az
sűrűségmátrix az 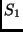 részrendszer
Hilbert-terén ható lineáris, önadjungált, pozitív szemidefinit operátor,
definíciója
részrendszer
Hilbert-terén ható lineáris, önadjungált, pozitív szemidefinit operátor,
definíciója
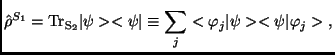 |
|
|
(2) |
ahol
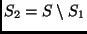 az
az 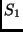 rendszer komplementer rendszere,
a
rendszer komplementer rendszere,
a 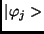 állapotok pedig teljes, ortonormált rendszert9 képeznek
állapotok pedig teljes, ortonormált rendszert9 képeznek
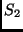 Hilbert-terében. (A
Hilbert-terében. (A
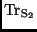 (``trace''=''nyom'') műveletet
a második egyenlőség definiálja, szemléletesen az
(``trace''=''nyom'') műveletet
a második egyenlőség definiálja, szemléletesen az 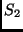 rendszer állapotaira
való kiátlagolásról van szó.) A sűrűségmátrix jelenti a kvantummechanikában
az állapotleírás legáltalánosabb módját. Speciálisan, ha a rendszernek van
rendszer állapotaira
való kiátlagolásról van szó.) A sűrűségmátrix jelenti a kvantummechanikában
az állapotleírás legáltalánosabb módját. Speciálisan, ha a rendszernek van
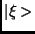 hullámfüggvénye, akkor
hullámfüggvénye, akkor
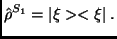 |
|
|
(3) |
Ilyenkor azt mondjuk, hogy az 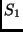 rendszer tiszta állapotban van.
rendszer tiszta állapotban van.
Ha az 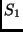 rendszer a
rendszer a 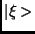 tiszta állapotban van, az
tiszta állapotban van, az
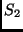 rendszer pedig a
rendszer pedig a 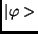 tiszta állapotban van,
akkor a két rendszer együttese, az
tiszta állapotban van,
akkor a két rendszer együttese, az 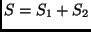 rendszer
a
rendszer
a
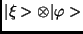 tiszta állapotban van. Itt
a
tiszta állapotban van. Itt
a 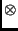 az ún. direkt szorzat
jele.10 Két diszjunkt rendszer egyesítésekor
az egyesített rendszer Hilbert-tere az első ill. a második
alrendszer állapotainak direkt szorzataiból épül fel.
az ún. direkt szorzat
jele.10 Két diszjunkt rendszer egyesítésekor
az egyesített rendszer Hilbert-tere az első ill. a második
alrendszer állapotainak direkt szorzataiból épül fel.



Next: Mérési axiómák
Up: Kvantummechanika dióhéjban
Previous: Kvantummechanika dióhéjban
Gyula Bene
2002-02-15
![]() -vel7. A mozgásegyenlet a (zárt rendszerre érvényes)
Schrödinger-egyenlet,
-vel7. A mozgásegyenlet a (zárt rendszerre érvényes)
Schrödinger-egyenlet,
![]() rendszer a
rendszer a ![]() tiszta állapotban van, az
tiszta állapotban van, az
![]() rendszer pedig a
rendszer pedig a ![]() tiszta állapotban van,
akkor a két rendszer együttese, az
tiszta állapotban van,
akkor a két rendszer együttese, az ![]() rendszer
a
rendszer
a
![]() tiszta állapotban van. Itt
a
tiszta állapotban van. Itt
a ![]() az ún. direkt szorzat
jele.10 Két diszjunkt rendszer egyesítésekor
az egyesített rendszer Hilbert-tere az első ill. a második
alrendszer állapotainak direkt szorzataiból épül fel.
az ún. direkt szorzat
jele.10 Két diszjunkt rendszer egyesítésekor
az egyesített rendszer Hilbert-tere az első ill. a második
alrendszer állapotainak direkt szorzataiból épül fel.