- ... vannak1
- Az éter
feltételezése még így is csak
bonyolult elmélet és számos ad hoc feltevés árán magyarázná,
hogy miért nem észlelték Michelson és Morley nevezetes kísérletükben
a Föld mozgását az éterhez képest.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tértől2
- A speciális (1905)[1] és általános relativitáselmélet (1915)
[2] szerint.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
lehetetlenségéről3
- A
félreértések elkerülése érdekében hadd tegyük hozzá: ez nem csupán a
mérési eljárás gyakorlati vagy akár elvi korlátozottsága. Szigorú
tétel bizonyítja[7], [8],
hogy már az a puszta feltevés is
ellentmondásra vezet, hogy a kanonikusan konjugált mennyiségeknek
a valóságban esetleg mégiscsak egyidejűleg pontos - habár kísérletileg
nem meghatározható - értéke létezik.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... érvényes4
- A ma rendelkezésre álló kísérleti eredmények
alapján ezt nincs okunk feltételezni.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
alapulnak.5
- Voltaképpen a kvantummechanika egy olyan módosításáról
van szó, amely önálló, a klasszikus fizikától független
elveken alapul, ezért nem tartalmazza a mérési axiómákat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... eleme.6
- Hilbert-térnek a teljes
euklideszi (azaz skalárszorzattal ellátott) komplex vektorteret nevezzük.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...-vel7
- A Dirac-féle jelöléseket használjuk. A
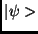 ún. ket-vektor adjungáltja a
ún. ket-vektor adjungáltja a 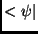 bra-vektor, mellyel a
bra-vektor, mellyel a
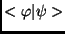 skalárszorzat (általában komplex szám) és a
skalárszorzat (általában komplex szám) és a
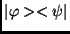 diadikus szorzat (a Hilbert-téren ható operátor)
kifejezhető.
diadikus szorzat (a Hilbert-téren ható operátor)
kifejezhető.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ope\-rá\-to\-rok8
- Egy lineáris
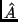 operátor egy állapotot
egy másik állapotba képez le lineárisan. Ha tehát
operátor egy állapotot
egy másik állapotba képez le lineárisan. Ha tehát 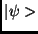 és
és 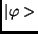 tetszőleges két állapot,
tetszőleges két állapot, 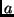 és
és 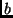 pedig tetszőleges komplex számok,
akkor
pedig tetszőleges komplex számok,
akkor
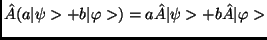 .
Az önadjungált operátort a
.
Az önadjungált operátort a
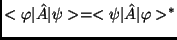 tulajdonság definiálja.
tulajdonság definiálja.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... rendszert9
-
Az ortonormáltság azt jelenti, hogy
a
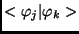 skalárszorzat nulla, ha
skalárszorzat nulla, ha 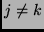 és egy, ha
és egy, ha 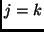 .
A teljesség azt jelenti, hogy
.
A teljesség azt jelenti, hogy
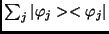 az adott Hilbert-térbeli egységoperátorral egyenlő.
az adott Hilbert-térbeli egységoperátorral egyenlő.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
jele.10
- A direkt szorzat mindkét tényezőjében lineáris leképezést
létesít az
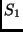 és
és 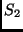 rendszerek Hilbert-terei és
az
rendszerek Hilbert-terei és
az 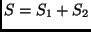 rendszer Hilbert-tere között. Fennáll tehát, hogy
rendszer Hilbert-tere között. Fennáll tehát, hogy
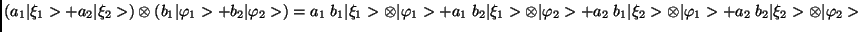
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kerül11
- Ez utóbbit
nem szükségszerű feltételezni, számos más, realisztikusabb előírás is
lehetséges. Mivel mondanivalónk lényegét nem érinti, most csak
a legegyszerűbb változatot használjuk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kiszámítható.12
- Ha csak a
lehetséges mérési eredményekre vagyunk
kíváncsiak, akkor persze elegendő az illető fizikai mennyiség operátorának
sajátértékeit meghatározni.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kapjuk.13
- Alkalmas kölcsönhatási Hamilton-operátort
választva ez valóban elérhető (időfüggő kölcsönhatási energia esetén
egzaktul, időfüggetlen kölcsönhatási energia esetén közelítőleg, de
tetszőleges pontossággal).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kimenetelét.14
- Ha feltételezünk egy további, de már klasszikusnak
tekintett (a határvonal túloldalán lévő) mérőeszközt, amellyel leolvassuk
az előző mérőeszköz által mutatott értéket, akkor a mérési axiómák
alkalmazása a várt eredményt adja.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... megfelel.''15
- Ezen a
kritériumon alapul a nevezetes EPR paradoxon.[15]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polarizációval.16
- Manapság ezt
alkalmas kristályra ejtett zöld lézerfénnyel
érik el. Nemlineáris optikai folyamat során egy zöld fotonból
két, különböző irányban haladó piros foton keletkezik, melyeknek polarizációi
erősen korreláltak.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
polarizációját.17
- Ezt itt nem bizonyítom általánosan.
Az állítás nyilvánvaló abban a speciális esetben, ha
a két foton együttes impulzusmomentuma nulla és ezzel
a korreláció 100%-os. Ilyenkor a másik foton ugyanolyan irányú
polarizációját lehet megjósolni.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... értékű18
- Azaz vagy rendelkezik az adott irányú polarizációval, és
ekkor az abba az irányba forgatott analizátoron keresztülmegy, vagy nem.
A foton az Einstein-Podolsky-Rosen-féle
realitás-kritérium szerint egyidejűleg végtelen sok polarizációval
rendelkezhet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... alkalmas.19
-
A
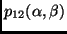 stb. mennyiségek kísérletileg meghatározhatók,
mint a kedvező és az összes esemény hányadosai.
Mivel azonban nehéz megbecsülni a veszteségeket, az összes esemény
száma pontatlan. A (22) képletből viszont az összes esemény
száma kiesik, így annak pontatlansága nem jár következményekkel.
stb. mennyiségek kísérletileg meghatározhatók,
mint a kedvező és az összes esemény hányadosai.
Mivel azonban nehéz megbecsülni a veszteségeket, az összes esemény
száma pontatlan. A (22) képletből viszont az összes esemény
száma kiesik, így annak pontatlansága nem jár következményekkel.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... környezetén20
- Értelemszerűen ezek a környezetek magát a rendszert mindig tartalmazzák.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... léteznek.21
- Hasonló absztrakció vezet a klasszikus
fizikában a vonatkoztatási rendszertől függő fizikai mennyiségek fogalmához.
Ott a mérőeszközöket a vonatkoztatási rendszerhez rögzítjük, és a
vonatkoztatási rendszer választásától függő mérési eredményeket
a vonatkoztatási rendszertől függő fizikai mennyiségek (méréstől független)
létezésével magyarázzuk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... megoldása22
- Általában több, esetleg végtelen sok
megoldás létezik.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... izolált23
- Máskülönben a számítás során figyelembe kellene vennünk a mérőeszköz kölcsönhatását a környezetével.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tartalmazza.24
-
Ha ennek az állapotnak a létezését kísérletileg szeretnénk ellenőrizni,
a teljes kvantumos referenciarendszeren kellene olyan mérést
végrehajtanunk, amely annak állapotát nem zavarja meg. Ez azt jelentené,
hogy egyidejűleg minden szabadsági fokot - az összes a rendszerhez tartozó
atomot - kontrollálnunk kellene, ami teljességgel elképzelhetetlen.
Ugyanígy lehetetlennek bizonyul minden olyan próbálkozás, amely
valamiféle abszurd eredményre vezető megfigyelhető jóslatot (pl. a macska
``feltámasztása'' alkalmas egymást követő mérések segítségével)
kíván a (24) állapot létezéséből levezetni.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
jósolni25
- Ez az állapot egy meghatározott irányú polarizáció
operátorának sajátállapota, így ennek a
fizikai mennyiségnek
egyértelműen megfeleltethető. A ``fizikai mennyiség'' és ``állapot''
kifejezések közötti lényeges fogalmi különbség itt tehát nem okoz
nehézséget.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tekintetében.26
- Niels Bohr az EPR paradoxonra
adott válaszában azt állította, hogy az Einstein-Podolsky-Rosen-féle
realitás-kritérium
a ``rendszer bármi módon való megzavarása nélkül'' kifejezés
jelentésének tekintetében nem egyértelmű.[21]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... állapottal27
- A mérőeszköz önmagára vonatkozó állapota viszont igen!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fel.28
- Ez tehát a
a megfigyelő tulajdonsága.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lesz29
- Makroszkopikus skálán, mert természetesen
a koordináták és impulzusok szórásai továbbra is eleget tesznek a
Heisenberg-féle határozatlansági relációknak.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
észlelik30
- Mivel a megfigyeléshez használt fény hullámhossza
sokkal nagyobb,
mint a megfigyelt objektum de Broglie hullámhossza.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.