Azt gondolhatnánk, hogy talán csak türelmesen tovább kell kísérletezni, és végül mégiscsak sérülni fog a szuperpozíció elve. Azonban a kvantummechanikában nem csak ez okoz nehézséget. A másik probléma abból adódik, hogy általános érvényű, alapvető fizikai elvekből (lokalitás és realizmus) a kvantummechanikának ellentmondó következményeket lehet levezetni. Ezen nem segít a szuperpozíció elv sérülése, annál is kevésbé, mivel a kvantummechanika idevágó, kísérletileg igazolt eredményei éppen a szuperpozíció-elv érvényességén alapulnak.
Mit értünk itt lokalitáson és realizmuson, és miként mondanak ellent a kvantummechanikának?
A lokalitás elve a fizikai hatások véges sebességű, folytonos
terjedésével kapcsolatos. A pontosabb megfogalmazáshoz
tekintsünk két különböző téridőpontban végbemenő eseményt. Az egyik
téridőpont
![]() , a másik
, a másik
![]() .
Mivel fizikai hatások nem terjedhetnek gyorsabban a
.
Mivel fizikai hatások nem terjedhetnek gyorsabban a
![]() fénysebességnél, ha a két esemény
térszerűen elválasztott, azaz
fénysebességnél, ha a két esemény
térszerűen elválasztott, azaz
![]() ,
akkor az események nem gyakorolhatnak egymásra semmilyen hatást.
,
akkor az események nem gyakorolhatnak egymásra semmilyen hatást.
Ebből azonban nem következik, hogy ezek az események függetlenek. Lehetséges ugyanis, hogy egy harmadik, egyiktől sem térszerűen elválasztott esemény gyakorolt mindkettőre befolyást. Valóban, ha pl. a rádióban a Kossuth-krónikát hallgatom, és ugyanekkor a szomszéd ugyanezt a műsort hallja a saját rádiójában, akkor ezt nem annak tulajdonítjuk, hogy az én rádióm volt hatással az övére, vagy az övé az enyémre, hanem annak, hogy mindkettőre az ugyanabból a központi műsorszóró adóantennából származó rádióhullám hatott. Más hullámhosszon és ``más műsorral'', de ugyanez a helyzet a Bell-egyenlőtlenség sérülését tesztelő kísérletekben (ld. alább). A realizmuson hétköznapi értelemben általában azt értjük, hogy hogy a körülöttünk levő világ a mi észleléseinktől függetlenül létezik. A jelen összefüggésben egy ennél speciálisabb követelményt szoktak realizmuson érteni, mégpedig az Einstein-Podolsky-Rosen-féle realitás-kritériumot.[15] Ez a következő: ``Ha egy rendszer bármi módon való megzavarása nélkül bizonyossággal, azaz egységnyi valószínűséggel meg tudjuk jósolni egy [hozzátartozó] fizikai mennyiség értékét, akkor létezik a fizikai valóságnak olyan eleme, amelyik ennek a fizikai mennyiségnek megfelel.''15Alkalmazzuk most ezt a két elvet egy egyszerű kísérlet elemzésekor! Tegyük fel, hogy közös fényforrásból ellentétes irányban repül ki két foton, közelítőleg ellentétes polarizációval.16 A kétfoton-rendszer kvantummechanikai állapota ismert, ami alapján az egyik foton adott irányú polarizációjának megmérésével bizonyossággal meg tudjuk jósolni a másik foton valamilyen irányú polarizációját.17
A lokalitás elvéből következik, hogy a két foton a forrásból való
távozás után nem befolyásolhatja egymás állapotát.
Az egyes fotonoknak megfelelő téridőpontok ugyanis (a közös forrást
tekintve a térbeli origónak)
![]() ill.
ill.
![]() .
Mivel
.
Mivel ![]() és
és ![]() nem azonos irányúak,
nem azonos irányúak,
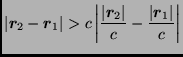 |
(12) |
Látható, hogy az Einstein-Podolsky-Rosen-féle realitás-kritérium feltételei teljesülnek: az első fotonon végzett mérés a második fotont semmi módon nem zavarja meg, ugyanakkor a mérés eredménye ismeretében a második foton egy meghatározott irányú polarizációja biztonsággal megjósolható. A realitás-kritérium alapján ezért a következtetésre jutunk, hogy a második foton egy bizonyos irányú polarizációja a méréstől függetlenül, objektíven létezik. Ha az első fotonon a korábbitól eltérő irányban mérjük meg a polarizációt, akkor másik irányú polarizációt lehet megjósolni. A gondolatmenet megismétlése arra vezet, hogy a második fotonnak - méréstől függetlenül - egyidejűleg bármely irányú polarizációja határozott értékű 18. Ha a fotonnak van adott irányú polarizációja, akkor azt fogjuk mondani, hogy az adott irányú polarizáció értéke 1, egyébként a polarizáció értéke 0. Ha a második fotonon végezzük a méréseket, akkor ugyanerre a következtetésre jutunk az első fotonnal kapcsolatban.
Ezek alapján kijelenthetjük, hogy minden egyes kísérletben
az egyik fotonnak ![]() polarizációja van az
polarizációja van az
![]() irányban, ugyanakkor
irányban, ugyanakkor ![]() polarizációja van az
polarizációja van az
![]() irányban, míg a másik fotonnak
irányban, míg a másik fotonnak ![]() polarizációja van a
polarizációja van a ![]() irányban és
irányban és ![]() polarizációja van a
polarizációja van a
![]() irányban. Az irányok
a terjedés irányára merőleges síkban vannak megadva,
az
irányban. Az irányok
a terjedés irányára merőleges síkban vannak megadva,
az ![]() ,
, ![]() ,
, ![]() ,
, ![]() polarizációk értéke pedig 0 vagy 1 lehet.
polarizációk értéke pedig 0 vagy 1 lehet.
A kísérletet sokszor ismételve valamekkora relatív gyakorisága,
végtelen sok mérésre extrapolálva pedig valószínűsége lesz
a fenti eseménynek. Jelöljük ezt ![]() -lel.
Nyilván
-lel.
Nyilván
| (14) |
| (15) | |||
| (16) | |||
| (17) |
| (18) | |||
| (19) |
| (20) |
| (21) |
Felvetődik, hogy hátha nem is igaz, amit a kvantummechanika jósol, és akkor mind a lokalitás, mind a realizmus fenntartható. De a kísérletek a perdöntő 1982-es Aspect-kísérlet[17], [18] óta egyre pontosabban és pontosabban a kvantummechanikai eredmény helyességét bizonyítják. A mérések pontosságát kb. húszezerszeresére[19], a fotonok által befutott utat pedig 10 méterről 11 kilométerre növelték [20]. A ma rendelkezésre álló kísérleti eredmények alapján tehát arra kell következtetnünk, hogy a két elv valamelyikét kénytelenek vagyunk feladni.
Ma számos kutató ``arra szavazna'', hogy a lokalitás elve sérül. Csakhogy egyetlen olyan jelenség sem ismeretes, amely ezt közvetlenül bizonyítaná. Pl. nem lehetséges fénysebességnél gyorsabban jeleket küldeni. Ráadáasul ma minden, kísérleti bizonyítékok alapján elfogadott fundamentális fizikai elmélet, így a világot mai tudásunk szerint legpontosabban leíró standard modell is, eleget tesz a lokalitás elvének.
Mindezek után kínálkozik egy újfajta lehetőség, amit a kísérletek is erőteljesen sugallnak:
Tételezzük fel, hogy
Az csak a kérdés, hogy lehet-e ilyen feltevésekkel következetes, a rendelkezésre álló kísérleti tapasztalattal összhangban lévő fizikai elméletet létrehozni. Mint alább látni fogjuk, a válasz az, hogy igen.