Következtetés: a kaotikus rendszerek belső instabilitása, a kezdeti feltételre való exponenciális érzékenysége
gyakorlatilag meghiúsítja a fizikában szokásos előrejelzési sémát (véges pontosságú kezdőállapot ![]() mozgásegyenletek megoldása
mozgásegyenletek megoldása ![]() véges, de még kielégítő pontosságú végállapot).
Hosszabb időre egy kaotikus rendszer mozgásáról csak valószínűségi kijelentések tehetők.
véges, de még kielégítő pontosságú végállapot).
Hosszabb időre egy kaotikus rendszer mozgásáról csak valószínűségi kijelentések tehetők.
Valószínűségi leírás (![]() valószínűségsűrűség,
valószínűségsűrűség, ![]() valószínűségi mérték. Frobenius-Perron-egyenlet.)
valószínűségi mérték. Frobenius-Perron-egyenlet.)
A kaotikus rendszer (jelen esetben egydimenziós leképezés) pályáját hosszú ideig követve megvizsgáljuk, hogy a fázistér valamely kiválasztott tartományában a teljes idő hányad részét tölti a rendszer. Ezt a számot tekintjük az ott-tartózkodás valószínűségének.
Valószínűségi mérték: ![]() annak a valószínűsége, hogy az iterált pont
annak a valószínűsége, hogy az iterált pont ![]() -nél nem nagyobb.
-nél nem nagyobb.
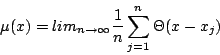
Valószínűségsűrűség: ![]() annak a valószínűsége, hogy az iterált pont
annak a valószínűsége, hogy az iterált pont ![]() és
és ![]() között tartózkodik.
között tartózkodik.
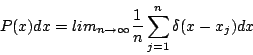
A Frobenius-Perron-egyenlet:
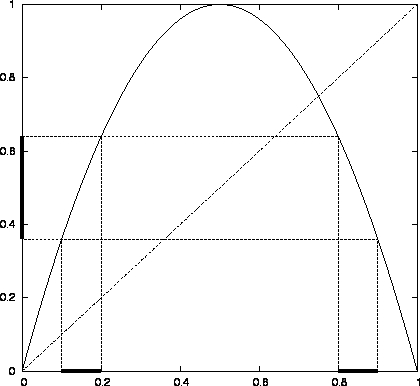 |
Példa: mind a háztető-leképezés, mind a Bernoulli-shift esetén ![]() , ezért a Frobenius-Perron-egyenlet:
, ezért a Frobenius-Perron-egyenlet:
Sima konjugálás (koordinátatranszformáció) hatása a valószínűségsűrűségre:
vagy
Példa: logisztikus leképezés.
![]() ,
, ![]() . Ezért
. Ezért
A Ljapunov-exponens kifejezése a stacionárius valószínűségsűrűséggel:
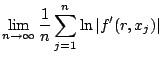 |
|||
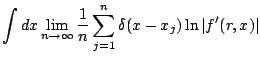 |
|||
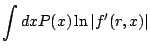 |
A Ljapunov-exponens nem változik sima konjugálás esetén:
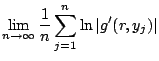 |
|||
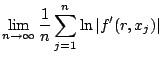 |
|||
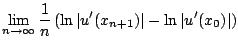 |
|||
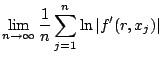 |
Feladat: mutassuk meg a Ljapunov-exponens sima konjugálásra vonatkozó invarianciáját a valószínűségsűrűséggel felírt alakból kiindulva!