


Next: Periodikus ablakok. Intermittencia. Krízis.
Up: Egydimenziós leképezések
Previous: Teljesen kifejlett káosz. Valószínűségeloszlás.
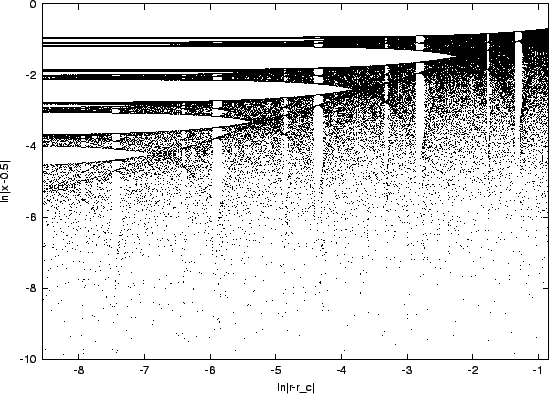
Ábra:
Hasonlóság a kaotikus tartományban: a logisztikus leképezés bifurkációs diagramja kétszer logaritmikus skálán.
 |
Sávkettéválások:
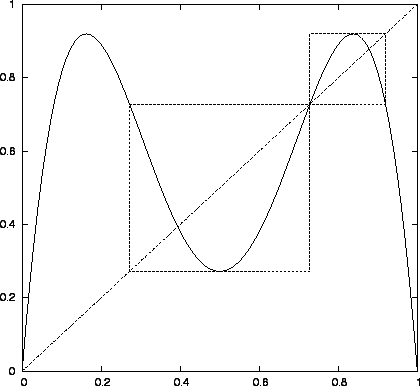
Ábra:
A logisztikus leképezés második iteráltja az első sávkettéválási pontban (
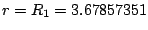 ).
).
 |
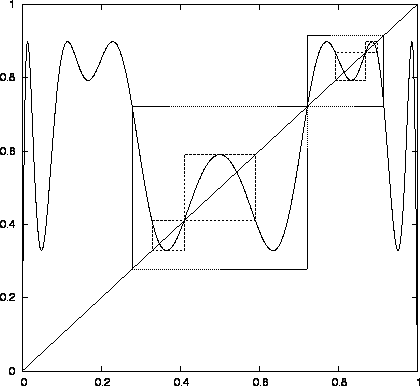
Ábra:
A logisztikus leképezés negyedik iteráltja a második sávkettéválási pontban (
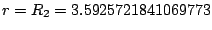 ).
).
 |
Az 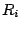 sávkettéválási pontoknak a határértékhez tartását ugyanaz a
sávkettéválási pontoknak a határértékhez tartását ugyanaz a 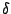 Feigenbaum-állandó jellemzi, mint
a perióduskettőző bifurkációkét:
Feigenbaum-állandó jellemzi, mint
a perióduskettőző bifurkációkét:
A sávok szélességét a sávkettéválás pontjaiban összehasonlítva az 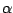 Feigenbaum-állandót kapjuk:
Feigenbaum-állandót kapjuk:
A sávkettéválásokhoz a perióduskettőződés esetével azonos módon definiálhatunk univerzális függvényeket,
melyeket a renormálási transzformáció visz egymásba.
Bene Gyula
2004-05-10


![\begin{displaymath}\lim_{k\rightarrow \infty} \frac{\left\vert f^{\left[2^{k-1}\...
...ht]}(R_{k+1},x_{max})-x_{max}\right\vert}=\alpha=2.502907875...\end{displaymath}](img190.png)